Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Hệ tọa độ trong không gian (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Hệ tọa độ trong không gian

Câu 1: Cho 3 vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\]. đều khác \[\vec{0}\]. Ba vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đồng phẳng khi và chỉ khi:

A. Giá của \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] cùng song song song với một mặt phẳng.

B. \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] cùng nằm trong một mặt phẳng.

C. \[\vec{a}\] nằm trong mặt phẳng (P), giá của \[\vec{b}\] và \[\vec{c}\] song song với (P)

D. Ba câu A, B và C

Lời giải:

A, B, C đúng.

Đáp án cần chọn là: D

Câu 2: Cho 3 vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đều khác \[\vec{0}\].  Ba vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đồng phẳng khi và chỉ khi:

A. \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] cùng nằm trong một mặt phẳng.

B. \[\exists m,\,\,n\,\,\in \mathbb{R}:\,\,\vec{a}=m\vec{b}+n\vec{c}\]

C. \[\vec{a}\] và \[\vec{b}\]cùng nằm trong mặt phẳng (P) và giá của \[\vec{c}\] cắt (P)

D. Hai câu A và B

Lời giải:

A và B đúng

Đáp án cần chọn là: D

Câu 3: : Cho 3 vector \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đều khác \[\vec{0}\]. Ba vector \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đồng phẳng khi và chỉ khi:

A. \[\exists m,\,\,n,\,\,p\,\,\in \mathbb{R}:\,\,m\vec{a}+n\vec{b}+p\vec{c}=0\]

B. \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] cùng vuông góc với \[\vec{d}\ne \vec{0}\] và \[\vec{d}\] có giá vuông góc với \[mp(P)\]

C. \[\vec{a}\] và \[\vec{b}\]cùng nằm trong mặt phẳng (Q) và \[\vec{c}\] có giá vuông góc (Q)

D. Hai câu A và B

Lời giải:

$m,n,p\ne 0$ . Suy ra A sai.

$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ cùng vuông góc với $\overrightarrow{d}$ và $\overrightarrow{d}$ vuông góc với $\left( P \right)$ nên giá của $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ cùng song song với $\left( P \right)$. Suy ra B đúng.

Đáp án cần chọn là: B

Câu 4: Cho 3 vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đều khác \[\vec{0}\]. Ba vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đồng phẳng khi và chỉ khi:

A. \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] có giá cùng vuông góc với một mặt phẳng

B. \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] có giá chéo nhau

C. \[\vec{a}\] trong mặt phẳng (R), \[\vec{b}\] và \[\vec{c}\] có giá cùng vuông góc với (R)

D. \[m,\,\,n,\,\,p\,\,\in \mathbb{R}:\,\,m\vec{a}+n\vec{b}+p\vec{c}=0\Leftrightarrow m=n=p=0\]

Lời giải:

Giá của $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$cùng vuông góc với $\left( S \right)$ nên chúng song song với bất kỳ mặt phẳng nào vuông góc với $\left( S \right)$. Suy ra A đúng

D $\Rightarrow $ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ không đồng phẳng.

Đáp án cần chọn là: A

Câu 5: Cho 3 vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đều khác \[\vec{0}\]. Ba vectơ \[\vec{a},\,\,\vec{b},\,\,\,\vec{c}\] đồng phẳng khi và chỉ khi:

A. Hệ phương trình \[\left\{ \begin{array}{l}m{b_1} + n{c_1} = {a_1}\\m{b_2} + n{c_2} = {a_2}\\m{b_3} + n{c_3} = {a_3}\end{array} \right.\] có nghiệm \[m,\,\,\,n\]

B. Hệ phương trình \[\left\{ \begin{array}{l}m{b_1} + n{c_1} + p{c_1} = 0\\m{b_2} + n{c_2} + p{c_2} = 0\\m{b_3} + n{c_3} + p{c_3} = 0\end{array} \right.\] có nghiệm \[m,\,\,n,\,\,p\] khác 0

C. \[\forall \vec{V},\,\,\exists \alpha ,\,\beta ,\,\,\gamma \in \mathbb{R}:\vec{V}=\alpha \vec{a}+\beta \vec{b}+\gamma \vec{c}\]

D. Hai câu A và B

Lời giải:

A và B đúng. C $\Rightarrow $ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ không đồng phẳng.

Đáp án cần chọn là: D

Câu 6: Trong hệ trục chuẩn Oxyz:

A. Điểm \[M\left( x,y,z \right)\] được biểu thị bởi \[\overrightarrow{OM}=x\overrightarrow{{{e}_{1}}}+y\overrightarrow{{{e}_{2}}}+z\overrightarrow{{{e}_{3}}}\]

B. Vectơ \[\vec{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right)\] được biểu thị bởi \[\vec{a}={{a}_{1}}\overrightarrow{{{e}_{1}}}+{{a}_{2}}\overrightarrow{{{e}_{2}}}+{{a}_{3}}\overrightarrow{{{e}_{3}}}\]

C. Vectơ \[\overrightarrow{AB}\] được biểu thị bởi \[\overrightarrow{AB}=\left( {{x}_{A}}-{{x}_{B}} \right)\overrightarrow{{{e}_{1}}}+\left( {{y}_{A}}-{{y}_{B}} \right)\overrightarrow{{{e}_{2}}}+\left( {{z}_{A}}-{{z}_{B}} \right)\overrightarrow{{{e}_{3}}}\] với \[A=\left( {{x}_{A}},{{y}_{A}},{{z}_{A}} \right)\] và \[B=\left( {{x}_{B}},{{y}_{B}},{{z}_{B}} \right)\]

D. Hai câu A và B

Lời giải:

A và B đúng

Đáp án cần chọn là: D

Câu 7: Trong không gian Oxyz cho vectơ  \[\vec{a}\ne \vec{0}\] và \[\left| {\vec{a}} \right|=a\]. Gọi \[\alpha ,\,\beta ,\,\gamma \] lần lượt là ba góc tạo bởi \[\vec{a}\] với ba trục \[\overrightarrow{Ox},\,\,\overrightarrow{Oy},\,\,\overrightarrow{Oz}\]. Ta có:

A. \[\vec a = \left( {a\cos \alpha ,a\sin \beta ,a\tan \gamma } \right)\]

B. \[\vec a = \left( {a\cos \alpha ,a\cos \beta ,a\cos \gamma } \right)\]

C. \[\vec a = \left( {a\cos \alpha ,a\sin \beta ,a\tan \gamma } \right)\]

D. \[\vec a = \left( {a\sin \alpha ,a\sin \beta ,a\sin \gamma } \right)\]

Lời giải:

Dùng công thức hình chiếu vecto trên trục, ta có:

Đáp án cần chọn là: B

Câu 8: Cho M trên đường thẳng \[AB\] với \[A\left( {{x}_{A}},{{y}_{A}},{{z}_{A}} \right)\] và \[B\left( {{x}_{B}},{{y}_{B}},{{z}_{B}} \right)\]. Nếu \[\overrightarrow{AM}=k.\overrightarrow{BM}\] với \[k\ne -1\] thì tọa độ của M là:

A. \[x=\frac{{{x}_{A}}-k{{x}_{B}}}{1-k};y=\frac{{{y}_{A}}-k{{y}_{B}}}{1-k};z=\frac{{{z}_{A}}-k{{z}_{B}}}{1-k}\]

B. \[x=\frac{{{x}_{A}}-k{{x}_{B}}}{1+k};y=\frac{{{y}_{A}}-k{{y}_{B}}}{1+k};z=\frac{{{z}_{A}}-k{{z}_{B}}}{1+k}\]

C. \[x=\frac{{{x}_{A}}+k{{x}_{B}}}{1+k};y=\frac{{{y}_{A}}+k{{y}_{B}}}{1+k};z=\frac{{{z}_{A}}+k{{z}_{B}}}{1+k}\]

D. \[x=\frac{{{x}_{A}}+k{{x}_{B}}}{1-k};y=\frac{{{y}_{A}}+k{{y}_{B}}}{1-k};z=\frac{{{z}_{A}}+k{{z}_{B}}}{1-k}\]

Lời giải:

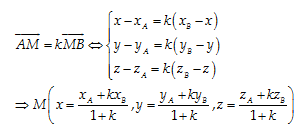
Đáp án cần chọn là: C

Câu 9: Trong không gian Oxyz cho hai vectơ \[\vec{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right),\,\,\,\vec{b}=\left( {{b}_{1}},{{b}_{2}},{{b}_{3}} \right)\] khác \[\vec{0}\] cùng phương. Câu nào sau đây sai?

A. \[\frac{{{a}_{1}}}{{{b}_{1}}}=\frac{{{a}_{2}}}{{{b}_{2}}}=\frac{{{a}_{3}}}{{{b}_{3}}}\]

B. \[\left\{ \begin{array}{l}{a_1}{b_2} - {a_2}{b_1} = 0\\{a_2}{b_3} - {a_3}{b_2} = 0\\{a_3}{b_1} - {a_1}{b_3} = 0\end{array} \right.\]

C. \[\left\{ \begin{array}{l}{a_1} = k{b_1}\\{a_2} = k{b_2}\\{a_3} = k{b_3}\end{array} \right.,\,\,\,k \in \mathbb{R}\]

D. Hai câu A và C

Lời giải:

A Sai vì thiếu điều kiện ${{b}_{1}},{{b}_{2}},{{b}_{3}}\ne 0$

B Đúng.

C Sai, vì thiếu điều kiện $k\in \mathbb{R}\backslash \left\{ 0 \right\}$

Đáp án cần chọn là: D

Câu 10: Trong không gian Oxyz cho hai vector \[\vec{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right),\,\,\,\vec{b}=\left( {{b}_{1}},{{b}_{2}},{{b}_{3}} \right)\] khác \[\vec{0}\]. Câu nào sau dây đúng?

A. \[\vec{a}.\vec{b}={{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}\]

B. \[\vec{a}\bot \vec{b}\Leftrightarrow {{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}=0\]

C. \[\vec{a}\] cùng phương \[\vec{b}\]\[\Leftrightarrow \cos \left( \vec{a},\vec{b} \right)=1\]

D. Hai câu A và B

Lời giải:

A và B đúng.

C sai, vì $\left( \overrightarrow{a},\overrightarrow{b} \right)=k\pi ,k\in \mathbb{Z}\Rightarrow \cos \left( \overrightarrow{a},\overrightarrow{b} \right)=\pm 1$

Đáp án cần chọn là: D

Câu 11: Trong không gian Oxyz, cho hai vectơ \[\vec{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right),\,\,\,\vec{b}=\left( {{b}_{1}},{{b}_{2}},{{b}_{3}} \right)\] khác \[\vec{0}\]. Tích hữu hướng của \[\vec{a}\] và \[\vec{b}\] là \[\vec{c}\]. Câu nào sau đây đúng?

A. \[\vec{c}=\left( {{a}_{1}}{{b}_{3}}-{{a}_{2}}{{b}_{1}},{{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}},{{a}_{3}}{{b}_{1}}-{{a}_{1}}{{b}_{3}} \right)\]

B. \[\vec{c}=\left( {{a}_{1}}{{b}_{3}}-{{a}_{3}}{{b}_{2}},{{a}_{3}}{{b}_{1}}-{{a}_{1}}{{b}_{3}},{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}} \right)\]

C. \[\vec{c}=\left( {{a}_{3}}{{b}_{1}}-{{a}_{1}}{{b}_{3}},{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}},{{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{1}} \right)\]

D. \[\vec{c}=\left( {{a}_{1}}{{b}_{3}}-{{a}_{3}}{{b}_{1}},{{a}_{2}}{{b}_{2}}-{{a}_{1}}{{b}_{2}},{{a}_{3}}{{b}_{2}}-{{a}_{2}}{{b}_{3}} \right)\]

Lời giải:

B đúng

Đáp án cần chọn là: B

Câu 12: Trong không gian Oxyz, cho hai vectơ \[\vec{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right),\,\,\,\vec{b}=\left( {{b}_{1}},{{b}_{2}},{{b}_{3}} \right)\] khác \[\vec{0}\]. Tích hữu hướng của \[\vec{a}\] và \[\vec{b}\] là \[\vec{c}\]. \[\cos \left( \widehat{\vec{a},\vec{b}} \right)\] là biểu thức nào sau đây?

A. \[\frac{{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}}{\left| {\vec{a}} \right|.\left| {\vec{b}} \right|}\]

B. \[\frac{{{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{3}}+{{a}_{3}}{{b}_{1}}}{\left| {\vec{a}} \right|.\left| {\vec{b}} \right|}\]

C. \[\frac{{{a}_{1}}{{b}_{3}}+{{a}_{2}}{{b}_{1}}+{{a}_{3}}{{b}_{2}}}{\left| {\vec{a}} \right|.\left| {\vec{b}} \right|}\]

D. \[\frac{{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{1}}}{\left| {\vec{a}} \right|.\left| {\vec{b}} \right|}\]

Lời giải:

A đúng

Đáp án cần chọn là: A

Câu 13: Trong hệ trục Descartes vuông góc Oxyz, cho tam giác ABC. Công thức diện tích tam giác ABC là:

A. \[S=\frac{1}{2}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right] \right|\]

B. \[S=\frac{1}{2}\left| \left[ \overrightarrow{BA},\overrightarrow{BC} \right] \right|\]

C. \[S=\frac{1}{2}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right] \right|\sin \left( \widehat{\overrightarrow{AB},\overrightarrow{AC}} \right)\]

D. Cả A, B, C.

Lời giải:

Cả bốn câu A, B, C, đều đúng

Đáp án cần chọn là: D

Câu 14: Cho hình hộp ABCD.DEFG trong không gian Oxyz. Thể tích hình hộp là công thức nào sau đây?

A. \[V=\left| \left[ \overrightarrow{AB}.\overrightarrow{AD} \right].\overrightarrow{AE} \right|\]

B. \[V=\left| \left[ \overrightarrow{BA}.\overrightarrow{BC} \right].\overrightarrow{BF} \right|\]

C. \[V=\left| \left[ \overrightarrow{CB}.\overrightarrow{CD} \right].\overrightarrow{CG} \right|\]

D. A, B, C đều đúng.

Lời giải:

Cả bốn câu A, B, C,  đều đúng.

Đáp án cần chọn là: D

Câu 15: Cho hình hộp ABCD.DEFG trong không gian Oxyz. Công thức thể tích hình chop EABD là:

A. \[V=\frac{1}{3}\left| \left[ \overrightarrow{AB}.\overrightarrow{AD} \right].\overrightarrow{AE} \right|\]

B. \[V=\frac{1}{3}\left| \left[ \overrightarrow{EA}.\overrightarrow{EA} \right].\overrightarrow{ED} \right|\]

C. \[V=\frac{1}{6}\left| \left[ \overrightarrow{AB}.\overrightarrow{AD} \right].\overrightarrow{AE} \right|\]

D. \[V=\frac{1}{12}\left| \left[ \overrightarrow{AB}.\overrightarrow{AD} \right].\overrightarrow{AE} \right|\]

Lời giải:

C đúng

Đáp án cần chọn là: C

Câu 16: Trong không gian Oxyz cho ba vectơ \[\vec{a},\,\,\vec{b}\] và \[\vec{c}\] khác \[\vec{0}\]. Câu nào sai?

A. \[\vec{a}\] cùng phương \[\vec{b}\]\[\Leftrightarrow \left[ \vec{a},\vec{b} \right]=0\]

B. \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] đồng phẳng \[\Leftrightarrow \left[ \vec{a},\vec{b} \right].\vec{c}=0\]

C. \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] không đồng phẳng \[\Leftrightarrow \left[ \vec{a},\vec{b} \right].\vec{c}\ne 0\]

D. \[\left| \left[ \vec{a},\vec{b} \right] \right|=\left| {\vec{a}} \right|.\left| {\vec{b}} \right|.\cos \left( \widehat{\vec{a},\vec{b}} \right)\]

Lời giải:

$\overrightarrow{a}$ cùng phương $\overrightarrow{b}\Leftrightarrow \left[ \overrightarrow{a},\overrightarrow{b} \right]=\overrightarrow{0}\Rightarrow $ A sai.

Đáp án cần chọn là: A

Câu 17: Trong không gian Oxyz cho tam giác ABC: biết \[A\left( 2,4,-3 \right);\,\,\overrightarrow{AB}=\left( -3,-1,1 \right);\,\,\overrightarrow{AC}=\left( 2,-6,6 \right)\]. Tìm tọa độ vectơ trung tuyến \[\overrightarrow{AM}\]

A. \[\left( 1,7,-7 \right)\]

B. \[\left( -1,-7,7 \right)\]

C. \[\left( \frac{1}{2},\frac{7}{2},-\frac{7}{2} \right)\]

D. \[\left( -\frac{1}{2},-\frac{7}{2},\frac{7}{2} \right)\]

Lời giải:

$\overrightarrow{AM}=\frac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AC} \right)\Leftrightarrow \overrightarrow{AM}=\left( -\frac{1}{2},-\frac{7}{2},\frac{7}{2} \right)$

Đáp án cần chọn là: D

Câu 18: Trong không gian Oxyz cho tam giác ABC: biết \[A\left( 2,4,-3 \right);\,\,\overrightarrow{AB}=\left( -3,-1,1 \right);\,\,\overrightarrow{AC}=\left( 2,-6,6 \right)\]. Tìm tọa độ vectơ trung tuyến \[\overrightarrow{AM}\]

A. \[\left( -\frac{5}{3},-\frac{5}{3},\frac{2}{3} \right)\]

B. \[\left( \frac{5}{3},\frac{5}{3},-\frac{2}{3} \right)\]

C. \[\left( \frac{7}{3},-\frac{1}{3},\frac{2}{3} \right)\]

D. \[\left( -1,3,-\frac{8}{3} \right)\]

Lời giải:

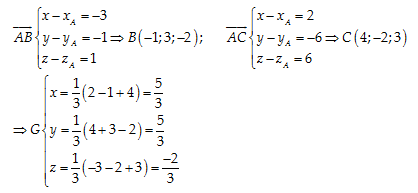
Đáp án cần chọn là: B

Câu 19: Trong không gian Oxyz cho tam giác ABC:

biết \[A\left( 2,4,-3 \right);\,\,\overrightarrow{AB}=\left( -3,-1,1 \right);\,\,\overrightarrow{AC}=\left( 2,-6,6 \right)\]. Tìm tọa độ điểm D sao cho ABCD là hình bình hành

A. \[\left( -7,1,-2 \right)\]

B. \[\left( 1,-3,4 \right)\]

C. \[\left( 7-,1,2 \right)\]

D. \[\left( -1,3,-4 \right)\]

Lời giải:

ABCD là hình bình hành $\Leftrightarrow \overrightarrow{AD}=\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$

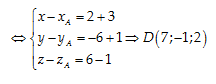
Đáp án cần chọn là: C

Câu 20: Trong không gian Oxyz cho tam giác ABC: biết \[A\left( 2,4,-3 \right);\,\,\overrightarrow{AB}=\left( -3,-1,1 \right);\,\,\overrightarrow{AC}=\left( 2,-6,6 \right)\]. Diện tích tam giác ABC bằng

A. \[20\sqrt{2}\] đvdt

B. \[40\sqrt{2}\] đvdt

C. \[5\sqrt{2}\] đvdt

D. \[10\sqrt{2}\] đvdt

Lời giải:

\(\begin{array}{l}4{S^2} = {\left| {\begin{array}{*{20}{c}}{ - 1}&1\\{ - 6}&6\end{array}} \right|^2} + {\left| {\begin{array}{*{20}{c}}1&{ - 3}\\6&2\end{array}} \right|^2} + \left| {\begin{array}{*{20}{c}}{ - 3}&{ - 1}\\2&{ - 6}\end{array}} \right| = 800\\ \Leftrightarrow {S^2} = 200 \Leftrightarrow S = 10\sqrt 2 \,\,dvdt\end{array}\)

Đáp án cần chọn là: D

Câu 21: Cho ba điểm \[A\left( 3,1,0 \right);\,\,\,B\left( 2,1,-1 \right);\,\,\,C\left( x,y,-1 \right)\]. Tìm tọa độ của C để ABC là tam giác đều

A. \[\left( 3,2,-1 \right)\]

B. \[\left( 3,0,-1 \right)\]

C. \[\left( -3,-2,1 \right);\,\,\,\left( 3,0,-1 \right)\]

D. \[\left( 3,2,-1 \right);\,\,\,\left( 3,0,-1 \right)\]

Lời giải:

Tam giác ABC đều

 \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}AC = AB\\BC = AB\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 6x - 2y + 9 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + {y^2} - 4x - 2y + 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\\\left( 2 \right) - \left( 1 \right):2x - 6 = 0 \Leftrightarrow x = 3 \Rightarrow {y^2} - 2y = 0 \Leftrightarrow y = 2 \vee y = 0\end{array}\)

Hai điểm $C\left( 3;2;-1 \right);C'\left( 3;0;-1 \right)$

Đáp án cần chọn là: D

Câu 22: Cho ba điểm \[A\left( 3,1,0 \right);\,\,\,B\left( 2,1,-1 \right);\,\,\,C\left( x,y,-1 \right)\]. Tìm tọa độ của C để tam giác ABC là tam giác vuông cân tại A

A. \[\left( 4,1+\sqrt{2} \right);\,\,\,\left( 4,1-\sqrt{2} \right)\]

B. \[\left( 4,1 \right)\]

C. \[\left( 2,1 \right)\]

D. \[\left( 2,-1 \right)\]

Lời giải:

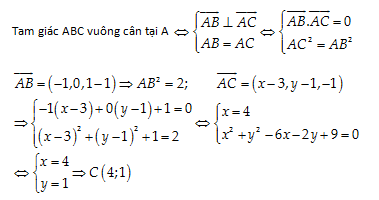
Đáp án cần chọn là: B

Câu 23: Cho ba điểm \[A\left( 3,1,0 \right);\,\,\,B\left( 2,1,-1 \right);\,\,\,C\left( x,y,-1 \right)\]. Tính  \[x\] và \[y\] để A, B, C thẳng hàng:

A. \[x=2,\,\,\,y=1\]

B. \[x=2,\,\,\,y=-1\]

C. \[x=-2,\,\,\,y=-1\]

D. \[x=1,\,\,\,y=2\]

Lời giải:

A, B, C thẳng thàng $\Leftrightarrow \overrightarrow{AB}$ cùng phương với $\overrightarrow{AC}$

\( \Leftrightarrow \left\{ \begin{array}{l}{a_1}{b_2} - {a_2}{b_1} = 0\\{a_2}{b_3} - {a_3}{b_2} = 0\\{a_3}{b_1} - {a_1}{b_3} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1\left( {y - 1} \right) - 0\left( {x - 3} \right) = 0\\0\left( { - 1} \right) - \left( { - 1} \right)\left( {y - 1} \right) = 0\\ - 1\left( {x - 3} \right) - \left( { - 1} \right)\left( { - 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Đáp án cần chọn là: A

Câu 24: Cho ba điểm \[A\left( 3,1,0 \right);\,\,\,B\left( 2,1,-1 \right);\,\,\,C\left( x,y,-1 \right)\]. Tính \[x,\,\,y\] để \[G\left( 2,-1,-\frac{2}{3} \right)\] là trọng tâm tam giác ABC

A. \[x=2,\,\,\,y=1\]

B. \[x=2,\,\,\,y=-1\]

C. \[x=-2,\,\,\,y=-1\]

D. \[x=1,\,\,\,y=-5\]

Lời giải:

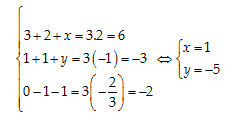
Đáp án cần chọn là: D

Câu 25: Cho ba điểm \[A\left( 2,-1,1 \right);\,\,B\left( 3,-2,-1 \right);\,\,\,C\left( 1,3,4 \right)\]. Tìm tọa độ giao điểm của đường thẳng AB và mặt phẳng (yOz)

A. \[\left( \frac{5}{2},-\frac{3}{2},0 \right)\]

B. \[\left( 0,-3,-1 \right)\]

C. \[\left( 0,1,5 \right)\]

D. \[\left( 0,-1,-3 \right)\]

Lời giải:

Gọi $M\left( 0,y,z \right)$ là giao điểm của đường thẳng AB và mặt phẳng $\left( yOz \right).$ Ta có $\overrightarrow{AM}=\left( -2,y+1,z-1 \right)$ và $\overrightarrow{AB}=\left( 1,-1,-2 \right)$ cùng phương.

$\Rightarrow \frac{-2}{1}=\frac{y+1}{-1}=\frac{z-1}{-2}\Rightarrow x=0;y=1;z=5\Rightarrow M\left( 0,1,5 \right)$

Đáp án cần chọn là: C

Câu 26: Cho ba điểm \[A\left( 2,-1,1 \right);\,\,B\left( 3,-2,-1 \right);\,\,\,C\left( 1,3,4 \right)\]. Tìm điểm N trên x’Ox cách đều A và B.

A. \[\left( 4,0,0 \right)\]

B. \[\left( -4,0,0 \right)\]

C. \[\left( 1,0,0 \right)\]

D. \[\left( 2,0,0 \right)\]

Lời giải:

Gọi $N\left( x,0,0 \right)$ trên $x'Ox.$ Ta có $A{{N}^{2}}=B{{N}^{2}}$

$\Leftrightarrow {{\left( x-2 \right)}^{2}}+{{\left( 1 \right)}^{2}}+{{\left( -1 \right)}^{2}}={{\left( x-3 \right)}^{2}}+{{\left( 2 \right)}^{2}}+{{1}^{2}}\Leftrightarrow x=4\Rightarrow N\left( 4,0,0 \right)$

Đáp án cần chọn là: A

Câu 27: Cho ba điểm \[A\left( 2,-1,1 \right);\,\,B\left( 3,-2,-1 \right);\,\,\,C\left( 1,3,4 \right)\]. Tìm điểm E trên mặt phẳng (xOy) cách đều A, B, C.

A. \[\left( \frac{14}{3},\frac{26}{3},0 \right)\]

B. \[\left( \frac{7}{3},\frac{13}{3},0 \right)\]

C. \[\left( \frac{26}{3},-\frac{14}{3},0 \right)\]

D. \[\left( \frac{26}{3},\frac{14}{3},0 \right)\]

Lời giải:

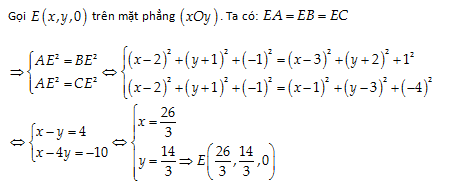
Đáp án cần chọn là: D

Câu 28: Cho ba điểm \[A\left( 10,9,12 \right);\,\,B\left( -20,3,4 \right);\,\,\,C\left( -50,-3,-4 \right)\]. Câu nào sau đây đúng?

A. A, B, C thẳng hàng

B. AB song song với (xOy)

C. AB cắt (xOy)

D. Hai câu A và C

Lời giải:

$\overrightarrow{AB}=\left( -30,-6,-8 \right);\,\,\overrightarrow{AC}=\left( -60,-12,-16 \right)\Rightarrow \overrightarrow{AC}=2\overrightarrow{AB}$

$\Rightarrow A,B,C$ thẳng hàng $\Rightarrow $ A đúng.

Giả sửu $AB$ và $\left( xOy \right)$ có điểm chung $M\left( x,y,0 \right)\Rightarrow \overrightarrow{AM}$ và $\overrightarrow{AB}$cùng phương $\Rightarrow \frac{x-10}{-30}=\frac{y-9}{-6}=\frac{-12}{-8}=\frac{3}{2}\Rightarrow M\left( x=-35,y=0,z=0 \right)\Rightarrow C$ đúng.

Đáp án cần chọn là: D

Câu 29: Cho tam giác ABC có \[A\left( -3,7,2 \right);\,\,B\left( 3,-1,0 \right);\,\,\,C\left( 2,2,-4 \right)\]. Gọi BD và BE lần lượt là phân giác trong và phân giác ngoài của góc B với D và E là chân của hai phân giác này trên AC. Tính tọa độ của D.

A. \[\left( -\frac{2}{3},2,-\frac{8}{3} \right)\]

B. \[\left( \frac{2}{3},-2,\frac{8}{3} \right)\]

C. \[\left( \frac{1}{3},\frac{11}{3},-2 \right)\]

D. \[\left( -\frac{1}{3},\frac{11}{3},2 \right)\]

Lời giải:

\(\left. \begin{array}{l}A{B^2} = 36 + 64 + 4 = 104 \Rightarrow AB = 2\sqrt {26} \\B{C^2} = 1 + 9 + 16 = 26 \Rightarrow BC = \sqrt {26} \end{array} \right\} \Rightarrow \frac{{BA}}{{BC}} = 2\)

D chia đoạn AC theo tỉ số $k=-2$ $\Rightarrow $ Tọa đô của D là:

$x=\frac{{{x}_{A}}-k{{x}_{C}}}{1-k}=\frac{-3+4}{3}=\frac{1}{3};\,\,y=\frac{7+4}{3}=\frac{11}{3};\,\,z=\frac{2-8}{3}=-2$

Đáp án cần chọn là: C

Câu 30: Cho tam giác ABC có \[A\left( -3,7,2 \right);\,\,B\left( 3,-1,0 \right);\,\,\,C\left( 2,2,-4 \right)\]. Gọi BD và BE lần lượt là phân giác trong và phân giác ngoài của góc B với D và E là chân của hai phân giác này trên AC. Tính tọa độ vectơ \[\overrightarrow{BE}\]

A. \[\left( -2,6,-8 \right)\]

B. \[\left( 4,-2,-10 \right)\]

C. \[\left( 4,2,10 \right)\]

D. \[\left( 2,-6,8 \right)\]

Lời giải:

Ta có $\overrightarrow{EA}=2\overrightarrow{EC}\Rightarrow C$ là trung điểm của AE.

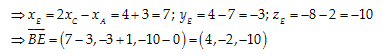
Đáp án cần chọn là: B

Câu 31: Cho tam giác ABC có \[A\left( -3,7,2 \right);\,\,B\left( 3,-1,0 \right);\,\,\,C\left( 2,2,-4 \right)\]. Gọi BD và BE lần lượt là phân giác trong và phân giác ngoài của góc B với D và E là chân của hai phân giác này trên AC. Cho bốn điểm \[A\left( -1,5,-10 \right);B\left( 5,-7,8 \right),C\left( 2,2,-7 \right)\] và \[D\left( 5,-4,2 \right)\]. Câu nào sau đây đúng? ABDC là:

A. Hình chóp

B. Tứ diện đều

C. Hình thang

D. Hình bình hành

Lời giải:

Ta có $\overrightarrow{AB}=\left( 6.-12,18 \right);\,\,\overrightarrow{CD}=\left( 3,-6,9 \right)\Rightarrow \overrightarrow{AB}=2\overrightarrow{CD}$

Do đó $\overrightarrow{AB}$ cùng phương $\overrightarrow{CD}\Rightarrow $ABDC là hình thang.

Đáp án cần chọn là: C

Câu 32: Ba vectơ \[\overrightarrow{MN},\overrightarrow{GI},\overrightarrow{KH}:\]

A. Bằng nhau

B. Đồng phẳng

C. Không đồng phẳng

D. Hai câu A và B

Lời giải:

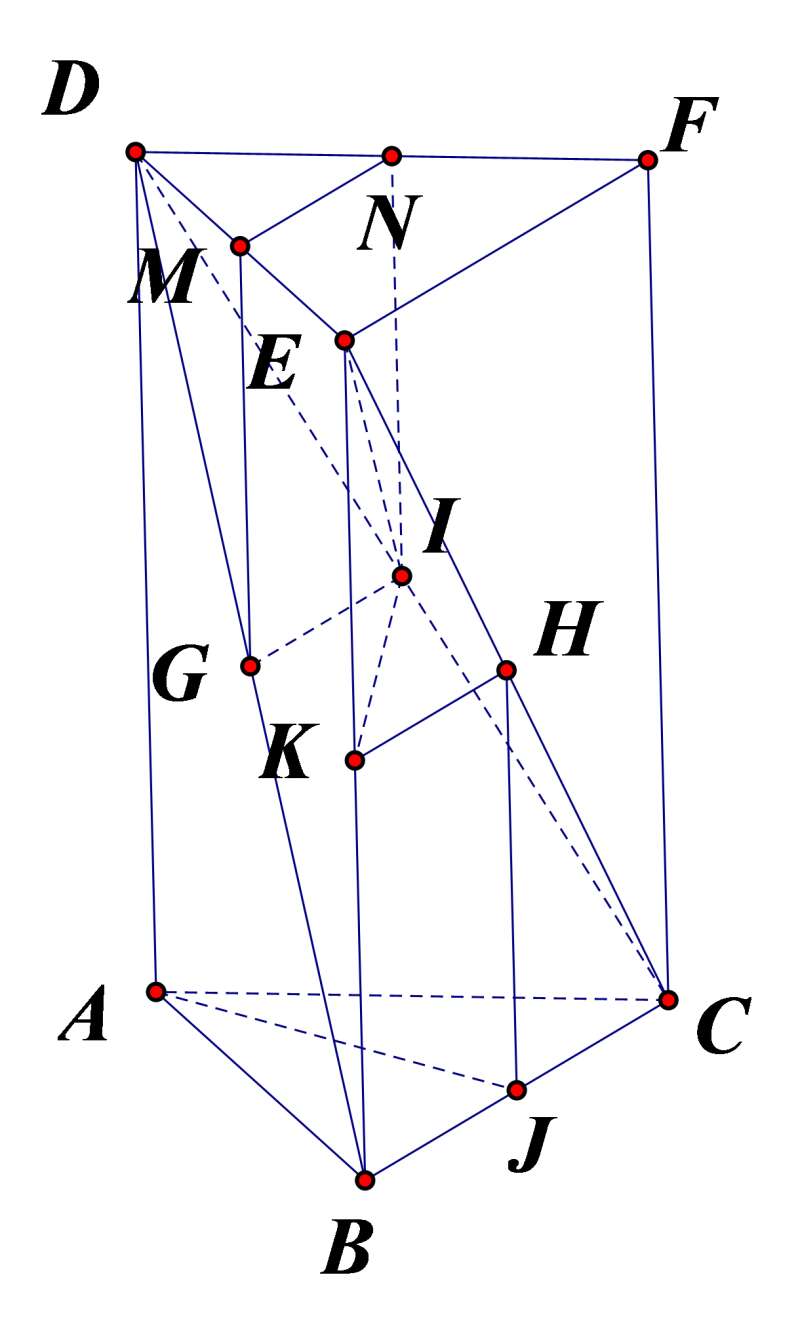
MN là đườn trung bình trong tam giác $DEF$: $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BC}$

Tương tự: $\overrightarrow{GI}=\frac{1}{2}\overrightarrow{BC}$ và $\overrightarrow{KH}=\frac{1}{2}\overrightarrow{BC}$

Vậy $\overrightarrow{MN}=\overrightarrow{GI}=\overrightarrow{KH}\Rightarrow $A và B đúng.

Đáp án cần chọn là: D

Câu 33: Ba vectơ \[\overrightarrow{MN},\,\overrightarrow{GI},\,\overrightarrow{KH}:\]

A. Không đồng phẳng

B. Đồng phẳng

C. Có môđun bằng nhau

D. Đôi một vuông góc

Lời giải:

$\overrightarrow{AJ}$ và $\overrightarrow{FM}$ lần lượt nằm trong hai mặt đáy song song ABC và DEF. $\overrightarrow{IK}$ đi qua trung điểm K của BE và tâm I của mặt bên ACFD, nên giá IK song song với hai mặt đáy ABC và DEF. Vậy $\overrightarrow{AJ},\overrightarrow{IK},\overrightarrow{FM}$ đồng phẳng. CHúng có giá chéo nhau, nhưng không vuông góc nhau và modun không bằng nhau.

Đáp án cần chọn là: B

Câu 34: Bốn vectơ \[\overrightarrow{MG},\,\overrightarrow{NI},\,\overrightarrow{HJ},\,\overrightarrow{KB}:\]

A. Không đồng phẳng

B. Bằng nhau

C. Đồng phẳng

D. Hai câu C và B

Lời giải:

MG là đường trung bình trong tam giác BDE: $\overrightarrow{MG}=\frac{1}{2}\overrightarrow{EB}=\overrightarrow{KB}$

Tương tự: $\overrightarrow{NI}=\frac{1}{2}\overrightarrow{FC}=\frac{1}{2}\overrightarrow{EB}=\overrightarrow{KB}$ và $\overrightarrow{HJ}=\frac{1}{2}\overrightarrow{EB}=\overrightarrow{KB}$

Vậy chúng đồng phẳng. Suy ra B và C đúng.

Đáp án cần chọn là: D

Câu 35: Nếu ABC.DEF là lăng trụ đều thì ba vectơ \[\overrightarrow{AJ},\,\overrightarrow{FM},\,\overrightarrow{EN}:\]

A. Đồng phẳng

B. Bằng nhau

C. Có môđun bằng nhau

D. Hai câu A và C

Lời giải:

$\overrightarrow{AJ}\subset \left( ABC \right);\,\,\overrightarrow{FM}$ và $\overrightarrow{EN}\subset \left( DEF \right);\left( ABC \right)//\left( DEF \right)\Rightarrow $ A đúng.

Hai đáy ABC và DEF là hai tam giác đều bằn nhau, nên các trung tuyến bằng nhau: $AJ=FM=EN\Rightarrow $ C đúng.

Đáp án cần chọn là: D

Câu 36: Ba vectơ \[\overrightarrow{a}=\left( 1,-2,3 \right);\overrightarrow{b}=\left( -3,-2,-1 \right);\overrightarrow{c}=\left( 1,3,-2 \right):\]

A. Có môđun bằng nhau

B. Đồng phẳng

C. Bằng nhau

D. Hai câu A và B

Lời giải:

${{\left| \overrightarrow{a} \right|}^{2}}=1+4+9=14,\,\,{{\left| \overrightarrow{b} \right|}^{2}}=9+4+1=14,\,\,{{\left| \overrightarrow{c} \right|}^{2}}=1+9+4=14$

$\Rightarrow {{\left| \overrightarrow{a} \right|}^{2}}={{\left| \overrightarrow{b} \right|}^{2}}={{\left| \overrightarrow{c} \right|}^{2}}\Rightarrow $A đúng.

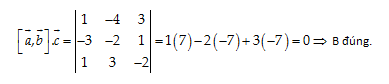
Đáp án cần chọn là: D

Câu 37: Tính thể tích hình lăng trụ ABCD.EFGH, biết \[\overrightarrow{AB}=\left( 2,-4,3 \right);\overrightarrow{EH}=\left( 3,-2,1 \right)\] và \[\overrightarrow{CG}=\left( -1,3,-2 \right)\].

A. 3 đvtt

B. 43 đvtt

C. 6 đvtt

D. 18 đvtt

Lời giải:

$\overrightarrow{AB}=\left( 2,-4,3 \right);\,\,\overrightarrow{AD}=\overrightarrow{EH}=\left( 3,-2,1 \right);\,\,\overrightarrow{AE}=\overrightarrow{CG}=\left( -1,3,-2 \right)$

Vậy \(V = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right].\overrightarrow {AE} } \right| = \left| {\left| {\begin{array}{*{20}{c}}2&{ - 4}&3\\3&{ - 2}&1\\{ - 1}&3&{ - 2}\end{array}} \right|} \right| = \left| {2 - 20 + 21} \right| = 3\)đvtt

Đáp án cần chọn là: A

Câu 38: Cho bốn vectơ \[\overrightarrow{a}=\left( 2,6,-1 \right);\overrightarrow{b}=\left( 2,1,-1 \right);\overrightarrow{c}=\left( -4,3,2 \right)\] và \[\overrightarrow{d}=\left( 2,11,-1 \right).\] Tìm tọa độ ba vectơ đồng phẳng.

A. \[\overrightarrow{a},\,\,\overrightarrow{b},\,\,\overrightarrow{c}\]

B. \[\overrightarrow{a},\,\,\overrightarrow{b},\,\,\overrightarrow{d}\]

C. \[\overrightarrow{a},\,\,\overrightarrow{c},\,\,\overrightarrow{d}\]

D. Cả 3 câu trên.

Lời giải:

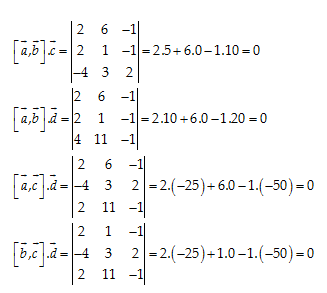
Đáp án cần chọn là: D

Câu 39: Cho ba vectơ \[\overrightarrow{a},\,\,\,\overrightarrow{b},\,\,\,\overrightarrow{c}\] khác \[\overrightarrow{0}\] thỏa mãn \[m\overrightarrow{a}\,\,+\,\,n\,\overrightarrow{b}\,\,+\,\,\,p\,\overrightarrow{c}\,\,=\,\,\overrightarrow{0}\,,\,\,\,\forall m,n,p\in \mathbb{R}.\] Câu nào đúng?

A. \[\overrightarrow{a},\,\,\,\overrightarrow{b},\,\,\,\overrightarrow{c}\] đồng phẳng \[\Leftrightarrow \,\,m,\,n,\,p\,\,\ne \,\,0\]

B. \[\overrightarrow{a},\,\,\,\overrightarrow{b},\,\,\,\overrightarrow{c}\] không đồng phẳng \[\Leftrightarrow \,\,m=\,n=p\,=\,0\]

C. \[\overrightarrow{a},\,\,\,\overrightarrow{b},\,\,\,\overrightarrow{c}\] đồng phẳng \[\Leftrightarrow \,\,m\ne \,0,\,\,\forall n,\,p\]

D. Hai câu A và B

Lời giải:

A và B đúng.

Đáp án cần chọn là: D

Câu 40: Cho hình chóp G.ABC có \[A\left( 0,2,2 \right);B\left( 0,1,2 \right);C\left( -1,1,1 \right);G\left( 1,-2,-1 \right).\] Thể tích hình chóp bằng :

A. 6 đvtt

B. 4 đvtt

C. \[\frac{2}{3}\] đvtt

D. 2 đvtt

Lời giải:

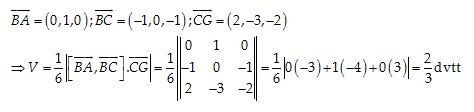
Đáp án cần chọn là: C

Câu 41: Cho hình chóp G.ABC có \[A\left( 0,2,2 \right);B\left( 0,1,2 \right);C\left( -1,1,1 \right);G\left( 1,-2,-1 \right).\] Tính thể tích hình hộp ABCD.EFGH có đáy ABCD chứa đáy ABC của hình chóp và đáy EFGH qua đỉnh G của hình chóp.

A. 8 đvtt

B. 4 đvtt

C. 6 đvtt

D. 3 đvtt

Lời giải:

$\overrightarrow{AB}=\left( 0;-1;0 \right);\,\,\overrightarrow{AD}=\overrightarrow{BC}=\left( -1;0;-1 \right);\overrightarrow{AE}=\overrightarrow{CG}=\left( 2;-3;-2 \right)$

$\Rightarrow V=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right].\overrightarrow{AE} \right|=\left| 0\left( -3 \right)-1\left( -4 \right)+0.3 \right|=4$ đvtt

Đáp án cần chọn là: B

Câu 42: Cho hình hộp chữ nhật OABD.DEFG có \[OA=a;\,\,OC=b;\,\,CD=c\]. Gọi I là tâm hình hộp. Biểu thị vectơ \[\overrightarrow{OI}\] theo ba vectơ \[\overrightarrow{OA},\,\,\overrightarrow{OC},\] và \[\overrightarrow{OD}\]

A. \[\overrightarrow{OI}\,\,=\,\,\overrightarrow{OA}\,\,+\,\,\overrightarrow{OC}\,\,+\overrightarrow{OD}\]

B. \[\overrightarrow{OI}\,\,=\,\,\overrightarrow{OA}\,\,-\,\,\overrightarrow{OC}\,\,+\overrightarrow{OD}\]

C. \[\overrightarrow{OI}\,\,=\,\,\frac{1}{2}\overrightarrow{OA}\,\,-\,\,\overrightarrow{OC}\,\,+\,\,\frac{1}{3}\overrightarrow{OD}\]

D. \[\overrightarrow{OI}\,\,=\,\,\frac{1}{2}(\overrightarrow{OA}\,\,+\,\,\overrightarrow{OC}\,\,+\overrightarrow{OD})\]

Lời giải:

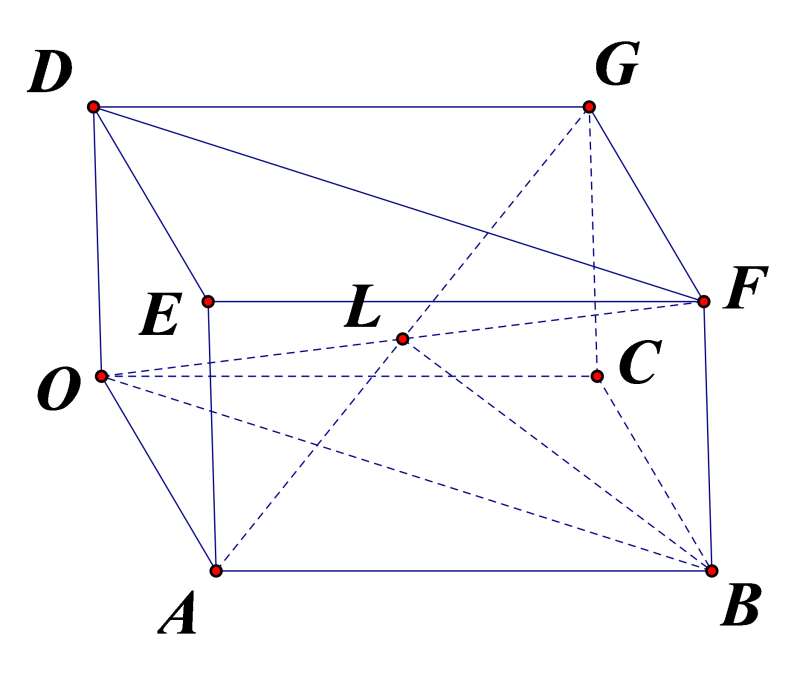
$I$ là trung điểm đường chéo $OF$

$\Rightarrow \overrightarrow{OI}=\frac{1}{2}\overrightarrow{OF}=\frac{1}{2}\left( \overrightarrow{OB}+\overrightarrow{BF} \right)=\frac{1}{2}\left( \overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OD} \right)$

$\Rightarrow \overrightarrow{OI}=\left( \frac{a}{2};\frac{b}{2};\frac{c}{2} \right)$

Đáp án cần chọn là: D

Câu 43: Cho hình hộp chữ nhật OABD.DEFG có \[OA=a;\,\,OC=b;\,\,CD=c\]. Gọi I là tâm hình hộp. Biểu thị vectơ \[\overrightarrow{BI}\] theo ba vectơ \[\overrightarrow{FE},\,\,\overrightarrow{FG}\] và \[\overrightarrow{FI}\]

A. \[\overrightarrow{BI}\,\,=\,\,\overrightarrow{FE}\,\,+\,\,\overrightarrow{FG}\,\,-\,\,\overrightarrow{FI}\]

B. \[\overrightarrow{BI}\,\,=\,\,\overrightarrow{FE}\,\,+\,\,\overrightarrow{FG}\,\,-\,\,2\overrightarrow{FI}\]

C. \[\overrightarrow{BI}\,\,=\,\,\overrightarrow{FE}\,\,+\,\,2\overrightarrow{FG}\,\,+\,\,3\overrightarrow{FI}\]

D. \[\overrightarrow{BI}\,\,=\,\,\frac{1}{2}\overrightarrow{FE}\,\,+\,\,\frac{3}{2}\overrightarrow{FG}\,\,+\,\,2\overrightarrow{FI}\]

Lời giải:

$\overrightarrow{BI}=\overrightarrow{BO}+\overrightarrow{OI}=\overrightarrow{FD}-\overrightarrow{FI}=\overrightarrow{FE}+\overrightarrow{FG}-\overrightarrow{FI}$

Đáp án cần chọn là: A

Câu 44: Cho hình hộp chữ nhật OABD.DEFG có \[OA=a;\,\,OC=b;\,\,CD=c\]. Gọi I là tâm hình hộp. Chọn hệ trục trực chuẩn Oxyz sao cho \[\overrightarrow{Ox},\,\,\overrightarrow{Oy},\,\,\overrightarrow{Oz}\] lần lượt là \[\overrightarrow{OA},\,\,\overrightarrow{OC},\,\,\overrightarrow{OD}\]. Tính tọa độ của \[\overrightarrow{IF}.\]

A. \[\left( 2a,b,c \right)\]

B. \[\left( a,\frac{b}{2},c \right)\]

C. \[\left( \frac{a}{2},\frac{b}{2},\frac{c}{2} \right)\]

D. \[\left( \frac{a}{2},b,2c \right)\]

Lời giải:

$\overrightarrow{IF}=\frac{1}{2}\overrightarrow{OF}=\frac{1}{2}\left( \overrightarrow{OB}+\overrightarrow{BF} \right)=\frac{1}{2}\left( \overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OD} \right)$

$\Rightarrow \overrightarrow{IF}=\left( \frac{a}{2};\frac{b}{2};\frac{c}{2} \right)$

Đáp án cần chọn là: C

Câu 45: Cho hình hộp chữ nhật OABD.DEFG có \[OA=a;\,\,OC=b;\,\,CD=c\]. Gọi I là tâm hình hộp. Tính tọa độ của \[\overrightarrow{AG}\].

A. \[\left( \frac{a}{2},-b,2c \right)\]

B. \[\left( a,\frac{b}{2},c \right)\]

C. \[\left( -a,\frac{b}{2},c \right)\]

D. \[\left( -a,b,c \right)\]

Lời giải:

$\overrightarrow{AG}=\overrightarrow{AC}+\overrightarrow{CG}=\overrightarrow{AO}+\overrightarrow{OC}+\overrightarrow{OD}$

$\Rightarrow \overrightarrow{AG}=\left( -a;b;c \right)$

Đáp án cần chọn là: D

Câu 46: Phân tích vectơ \[\overrightarrow{V}=\left( 4\,,\,3\,,\,-5\, \right)\] theo ba vectơ không đồng phẳng \[\overrightarrow{a}=\left( 2,-1,1 \right);\,\,\overrightarrow{b}=\left( 1,-3,2 \right);\,\,\overrightarrow{c}=\left( -3,2,-2 \right).\]

A. \[\overrightarrow{V}=\,\,31\overrightarrow{a}\,\,+\,\,2\overrightarrow{b}\,\,+\,\,20\overrightarrow{c}\]

B. \[\overrightarrow{V}=\,\,31\overrightarrow{a}\,\,-\,\,2\overrightarrow{b}\,\,+\,\,20\overrightarrow{c}\]

C. \[\overrightarrow{V}=\,\,21\overrightarrow{a}\,\,+\,\,2\overrightarrow{b}\,\,+\,\,10\overrightarrow{c}\]

D. \[\overrightarrow{V}=\,\,21\overrightarrow{a}\,\,-\,\,2\overrightarrow{b}\,\,-\,\,10\overrightarrow{c}\]

Lời giải:

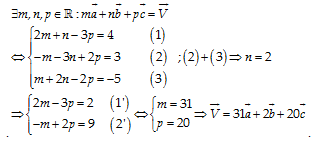
Đáp án cần chọn là: A

Câu 47: Tính góc của hai vectơ   \[\overrightarrow{a}=\,\left( -4,2,4 \right);\,\,\,\,\,\overrightarrow{b}=\,\left( 2\sqrt{2},-2\sqrt{2},0 \right)\]

A. \[{{60}^{0}}\]

B. \[{{135}^{0}}\]

C. \[{{30}^{0}}\]

D. \[{{120}^{0}}\]

Lời giải:

$\cos \left( \widehat{\overrightarrow{a};\overrightarrow{b}} \right)=\frac{-8\sqrt{2}-4\sqrt{2}+0}{\sqrt{36}.\sqrt{16}}=\frac{-\sqrt{2}}{2}\Rightarrow \left( \widehat{\overrightarrow{a};\overrightarrow{b}} \right)={{135}^{0}}$

Đáp án cần chọn là: B

Câu 48: Cho hai vectơ \[\overrightarrow{V}=\,m\overrightarrow{a}\,\,-\,\,2\overrightarrow{b}\] và \[\overrightarrow{W}=\,m\overrightarrow{b}\,\,-\,\,\overrightarrow{a}\] với \[\overrightarrow{a}=\left( 2,\,1,\,-1 \right)\] và \[\overrightarrow{b}=\left( 1,\,-2,\,1 \right)\]. Định m để \[\overrightarrow{V}\] và \[\overrightarrow{W}\] vuông góc.

A. \[-3\pm \sqrt{7}\]

B. \[3\pm \sqrt{7}\]

C. \[9\pm \sqrt{79}\]

D. \[-9\pm \sqrt{79}\]

Lời giải:

$\overrightarrow{V}$ vuông góc $\overrightarrow{W}\Leftrightarrow \left( m\overrightarrow{a}-2\overrightarrow{b} \right)\left( m\overrightarrow{b}-\overrightarrow{a} \right)=0\left( 1 \right)$

Với ${{\overrightarrow{a}}^{2}}=6;\,{{\overrightarrow{b}}^{2}}=6;\,\overrightarrow{a}.\overrightarrow{b}=-1$

$\left( 1 \right)\Leftrightarrow {{m}^{2}}+18m+2=0\Leftrightarrow m=-9\pm \sqrt{79}$

Đáp án cần chọn là: D

Câu 49: Cho hai vectơ \[\overrightarrow{V}=\,m\overrightarrow{a}\,\,-\,\,2\overrightarrow{b}\] và \[\overrightarrow{W}=\,m\overrightarrow{b}\,\,-\,\,\overrightarrow{a}\] với \[\overrightarrow{a}=\left( 2,\,1,\,-1 \right)\] và \[\overrightarrow{b}=\left( 1,\,-2,\,1 \right)\]. Với giá trị nào của m thì \[\overrightarrow{V}\] và \[\overrightarrow{W}\] cùng phương?

A. 2

B. -2

C. \[\sqrt{2}\]

D. \[\pm \sqrt{2}\]

Lời giải:

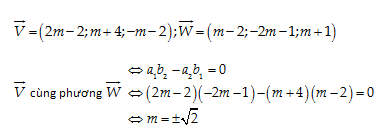
Đáp án cần chọn là: D

Câu 50: Cho hai vectơ \[\overrightarrow{a}=\,\,\left( 2,-1,1 \right);\,\,\overrightarrow{b}=\,\,\left( -2,3,1 \right).\] Xác định vectơ \[\overrightarrow{c}\], biết \[\overrightarrow{c}\] cùng phương với \[\overrightarrow{a}\] và \[\overrightarrow{a}.\overrightarrow{c}=\,\,-4\]

A. \[\left( -4,2,-2 \right)\]

B. \[\left( \frac{4}{3},-\frac{2}{3},\frac{2}{3} \right)\]

C. \[\left( -\frac{4}{3},\frac{2}{3},-\frac{2}{3} \right)\]

D. \[\left( -2,1,-1 \right)\]

Lời giải:

$\overrightarrow{c}=\left( {{c}_{1}};{{c}_{2}};{{c}_{3}} \right)$ cùng phương $\overrightarrow{a}\Leftrightarrow \frac{{{c}_{1}}}{2}=\frac{{{c}_{2}}}{-1}=\frac{{{c}_{3}}}{1}\Rightarrow {{c}_{1}}=2{{c}_{3}};\,{{c}_{2}}=-{{c}_{3}}$

$\overrightarrow{a}.\overrightarrow{c}=-4\Leftrightarrow 2{{c}_{1}}-{{c}_{2}}+{{c}_{3}}=-4\Leftrightarrow 4{{c}_{3}}+{{c}_{3}}+{{c}_{3}}=-4\Leftrightarrow {{c}_{3}}=-\frac{2}{3}$

$\Rightarrow {{c}_{1}}=2{{c}_{3}}=-\frac{4}{3};\,{{c}_{2}}=\frac{2}{3}\Rightarrow \overrightarrow{c}=\left( -\frac{4}{3};\frac{2}{3};-\frac{2}{3} \right)$

Đáp án cần chọn là: C