Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Phương trình đường thẳng trong không gian (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Phương trình đường thẳng trong không gian
Câu 1: Trong không gian Oxyz, một đường thẳng (d) có:
A. 1 vectơ chỉ phương duy nhất
B. 2 vectơ chỉ phương
C. 3 vectơ chỉ phương
D. Vô số vectơ chỉ phương.
Lời giải:
Chọn D
Đáp án cần chọn là: D
Câu 2: Trong không gian Oxyz, đường thẳng (d) qua M(x0,y0,z0) và có một vectơ chỉ phương →a=(a1,a2,a3) với a1,a2,a3≠0 có phương trình chính tắc là
A. x−x0a1=y−y0a2=z−z0a3
B. x+x0a1=y+y0a2=z+z0a3
C. x0−xa1=y0−ya2=z0−za3
D. x−x0a1=y−y0a2=z−z0a3
Lời giải:
A đúng
Đáp án cần chọn là: A
Câu 3: Trong không gian Oxyz, đường thẳng (d) có phương trình tổng quát là:
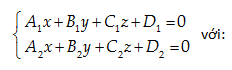
A. ∀A1,B1,C1,A2,B2,C2 thỏa A21+B21+C21>0, A22+B22+C22>0.
B. A1:B1:C1=A2:B2:C2
C. A1:B1:C1≠A2:B2:C2
D. A1=B1=C1=A2=B2=C2
Lời giải:
A đúng
Đáp án cần chọn là: A
Câu 4: Cho hai đường thẳng trong không gian Oxyz:(D):x−x1a1=y−y1a2=z−z1a3,(d):x−x2b1=y−y2b2=z−z2b3. Với a1,a2,a3,b1,b2,b3≠0. Gọi →a=(a1,a2,a3);→b=(b1,b2,b3) và →AB=(x2−x1,y2−y1,z2−z1). (D) và (d) cắt nhau khi và chỉ khi:
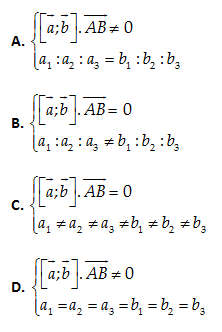
Lời giải:
[→a,→b].→AB=0⇒(D) và (d) cùng nằm trong một mặt phẳng a1:a2:a3≠b1:b2:b3⇔a1b1≠a2b2≠a3b3⇒(D) và (d) cắt nhau.
Đáp án cần chọn là: B
Câu 5: Cho hai đường thẳng trong không gian Oxyz:(D):x−x1a1=y−y1a2=z−z1a3,(d):x−x2b1=y−y2b2=z−z2b3. Với a1,a2,a3,b1,b2,b3≠0. Gọi →a=(a1,a2,a3);→b=(b1,b2,b3) và →AB=(x2−x1,y2−y1,z2−z1). (D) và (d) song song khi và chỉ khi:
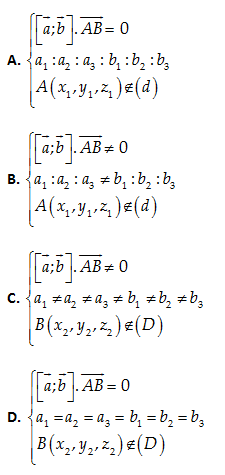
Lời giải:
[→a,→b].→AB=0⇒(D) và (d) cùng nằm trong một mặt phẳnga1:a2:a3=b1:b2:b3⇔a1b1=a2b2=a3b3⇒(D) và (d) cùng phương A(x1,y1,z1)∈(D) và A∉(d)⇒(D) và (d) song song.
Đáp án cần chọn là: A
Câu 6: Cho hai đường thẳng trong không gian Oxyz:(D):x−x1a1=y−y1a2=z−z1a3,(d):x−x2b1=y−y2b2=z−z2b3. Với a1,a2,a3,b1,b2,b3≠0. Gọi →a=(a1,a2,a3);→b=(b1,b2,b3) và →AB=(x2−x1,y2−y1,z2−z1). (D) và (d) chéo nhau khi và chỉ khi:
A. a1:a2:a3≠b1:b2:b3
B. a1:a2:a3=b1:b2:b3
C. [→a;→b].→AB=0
D. [→a;→b].→AB≠0
Lời giải:
[→a,→b].→AB≠0⇒(D) và (d) chéo nhau.
Đáp án cần chọn là: D
Câu 7: Cho mặt phẳng (P): Ax+By+Cz+D=0(A2+B2+C2>0) và đường thẳng (d):x−x0a1=y−y0a2=z−z0a3 (a1,a2,a3≠0). Câu nào sau đây sai?
A. Aa1+Ba2+Ca3≠0⇔(d) cắt (P)
B. a1:a2:a3=A:B:C⇔(d)⊥(P)
C. Aa1+Ba2+Ca3=0⇔(d)//(P)
D. Aa1+Ba2+Ca3=0 và Ax0+By0+Cz0+D=0⇔(d)⊂(P)
Lời giải:
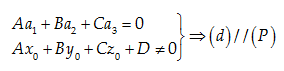
Đáp án cần chọn là: C
Câu 8: Góc của đường thẳng (D):x−x0a1=y−y0a2=z−z0a3(a1,a2,a3≠0) và mặt phẳng (P):Ax+By+Cz+D=0(A2+B2+C2>0) tính bởi công thức nào sau đây?
A. cosα=|Aa1+Ba2+Ca3|√A2+B2+C2.√a12+a22+a32
B. sinα=|Aa1+Ba2+Ca3|√A2+B2+C2.√a12+a22+a32
C. tanα=|Aa1+Ba2+Ca3|√A2+B2+C2.√a12+a22+a32
D. cotα=|Aa1+Ba2+Ca3|√A2+B2+C2.√a12+a22+a32
Lời giải:
B đúng
Đáp án cần chọn là: B
Câu 9: Để tính khoảng cách từ điểm M(x1,y1,z1) đến đường thẳng (D):x−x0a1=y−y0a2=z−z0a3(a1,a2,a3≠0), một học sinh lý luận qua các giai đoạn sau:
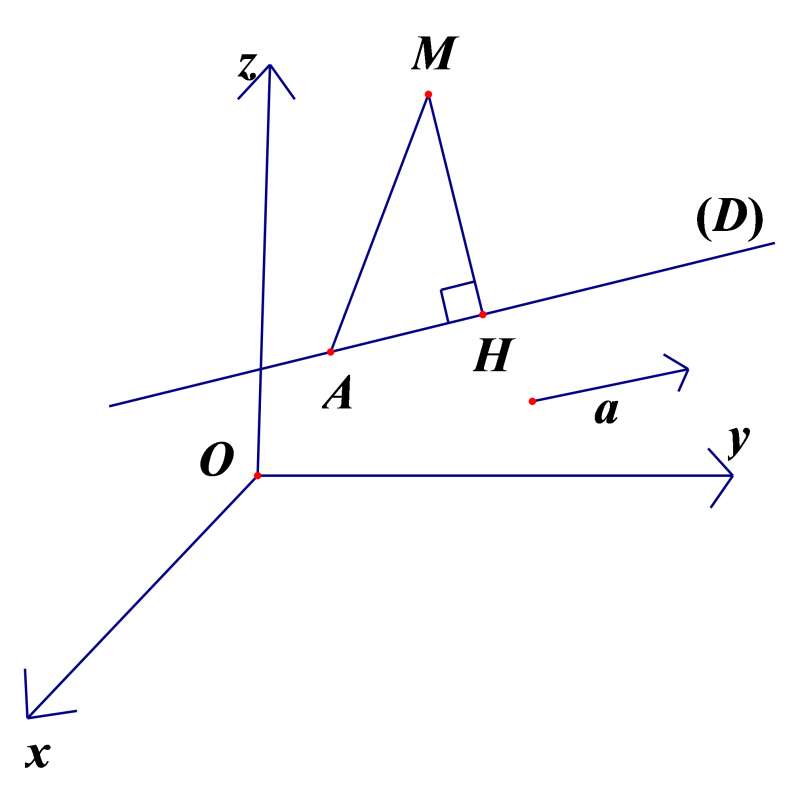
I. Vẽ MH vuông góc với (D) tại H. Ta có: A(x0,y0,z0)∈(D); vectơ chỉ phương của (D) là: →a=(a1,a2,a3).
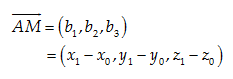
II. →AH cùng phương với →a, ta có: →AH=k→a
Diện tích tam giác AMH: S=12AH.MH=|k|.|→a|.MH2 (1)
III. Dùng tích hữu hướng, ta có diện tính tam giác AMH:
S=12|[→AH,→AM]|=|k|2.|[→a,→AM]| (2)
Từ (1) và (2), ta có : |→a|.MH=|[→a,→AM]|
Vậy d(M,D)=|[→a,→AM]||→a|
Lý luận trên đúng hay sai, nếu sai thì sai ở đoạn nào?
A. Chỉ I
B. Chỉ II
C. Chỉ III
D. Chỉ II và III
Lời giải:
Sai ở giai đoạn II, vì →AH=k→a thìk∈R∖{0}
Đáp án cần chọn là: C
Câu 10: Cho hai đường thẳng chéo nhau (D1):x−x1a1=y−y1a2=z−z1a3 và (D2):x−x2b1=y−y2b2=z−z2b3 (a1,a2,a3,b1,b2,b3≠0); với →a=(a1,a2,a3); →b=(b1,b2,b3) và →AB=(x2−x1,y2−y1,z2−z1).Khoảng cách hay đoạn vuông góc chung giữa (D1) và (D2) tính bởi công thức nào sau đây?
A. d(D1,D2)=|[→a,→b,→AB]||[→a,→b]|
B. d(D1,D2)=|[→a,→b]||[→a,→b,→AB]|
C. d(D1,D2)=|[→a,→b].→AB||[→a,→b]|
D. d(D1,D2)=|[→a,→b.→AB]||[→a,→b]|
Lời giải:
C đúng
Đáp án cần chọn là: C
Câu 11: Cho hai mặt phẳng (P):x−2y+3z−5=0;(Q):3x+4y−z+3=0. Đường thẳng (D) qua M(1,−2,3) song song với (P) và (Q).
A. (D) có một vec-tơ chỉ phương là →a=(−1,1,1)
B. (D) song song với mặt phẳng (R):3x+y+2z−12=0
C. (D) qua điểm N(3,−4,1)
D. (D) vuông góc với mặt phẳng (S):2x−2y−2z+3=0
Lời giải:
(D) song song với (P) và (Q)⇒ Một vectơ chỉ phương của (D) là:
→aP=[→nP,→nQ]=10(−1,1,1)⇒→a=(−1,1,1)
Pháp vectơ của (R):→nR=(3,1,2)⇒→a.→nR=−3+1+2=0⇒(D)//(R)
→NM=(−2,2,2)=2(−1,1,1)=2→a⇒(D)quaN(3,−4,1)
→ns=(2,−2,−2)⇒2−1=−21=−21=−2⇒→a cùng phương với →ns
⇒(D) vuông góc với (S).
Đáp án cần chọn là: D
Câu 12:
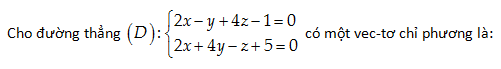
A. →a=(3,−2,−2)
B. →a=(−3,2,2)
C. →a=(−3,2,−2)
D. Hai câu A và B
Lời giải:
Pháp vectơ của hai mặt phẳng (P):2x−y+4z−1=0 và
(Q):2x+4y−z+5=0 là →n1=(2,−1,4);→n2=(2,4,−1).
Vectơ chỉ phương của \left( D \right) là \overrightarrow{{{a}_{D}}}=\left[ \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right]=-5\left( 3,-2,-2 \right)=5\left( -3,2,2 \right)
\Rightarrow \overrightarrow{a}=\left( 3,-2,-2 \right)\vee \overrightarrow{a}=\left( -3,2,2 \right)
Đáp án cần chọn là: D
Câu 13: Viết phương trình tham số của đường thẳng \left( D \right) qua hai điểm A\left( -1,3,-2 \right);B\left( 2,-3,4 \right)
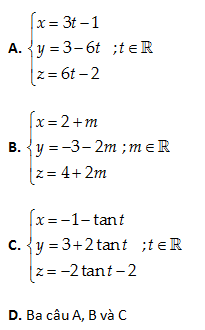
Lời giải:
Một vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\overrightarrow{AB}=\left( 3,-6,6 \right)=3\left( 1,-2,2 \right)=-3\left( -1,2,-2 \right)
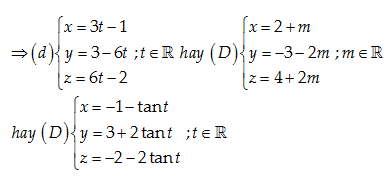
Đáp án cần chọn là: D
Câu 14: Viết phương trình tham số của đường thẳng (d) qua điểm E\left( 2,-4,3 \right) và song song với đường thẳng MN với M\left( 3,2,5 \right);N\left( 1,-1,2 \right).
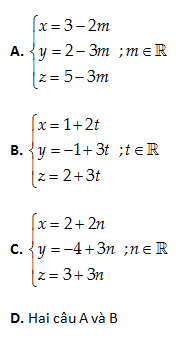
Lời giải:
Một vectơ chỉ phương của \left( d \right):\overrightarrow{MN}=\left( -2,-3,-3 \right)=-\left( 2,3,3 \right)
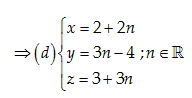
Đáp án cần chọn là: C
Câu 15:
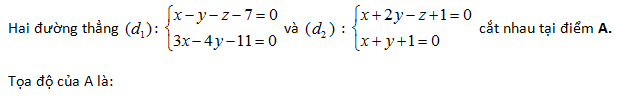
A. A(1,-2,-4)
B. A(-1,-2,-4)
C. A(1,2,-4)
D. A(1,-2,4)
Lời giải:
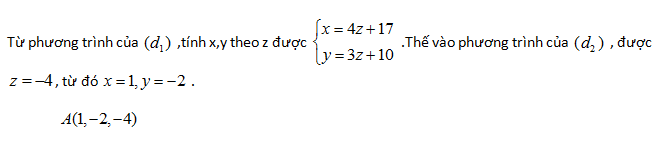
Đáp án cần chọn là: A
Câu 16: Viết phương trình tham số của đường thẳng (D) qua I\left( -1,5,2 \right) và song song với trục x'Ox
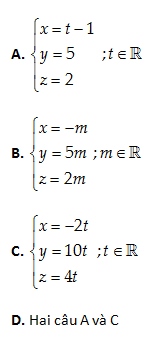
Lời giải:
\left( D \right)//x'Ox\Rightarrow Vectơ chỉ phương của \left( D \right):\overrightarrow{{{e}_{1}}}=\left( 1,0,0 \right)
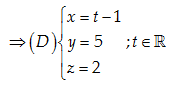
Đáp án cần chọn là: A
Câu 17: Viết phương trình tham số của đường thẳng (D) qua I\left( 1,-3,2 \right) và song song với đường thẳng \left( d \right):x=3+4t;y=2-2t;z=3t-1\left( t\in \mathbb{R} \right)
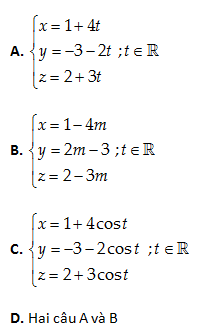
Lời giải:
\left( D \right)//\left( d \right) nên một vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\overrightarrow{{{e}_{1}}}=\left( 1,0,0 \right)\,\,hay\,\,\overrightarrow{a}=-\left( -1,0,0 \right)
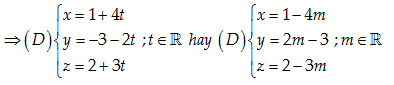
Đáp án cần chọn là: D
Câu 18: Viết phương trình tham số của đường thẳng (D) qua B\left( 5,2,-3 \right) và song song với đường thẳng \left( d \right):\frac{x+3}{2}=\frac{y-1}{3}=\frac{z+2}{4}
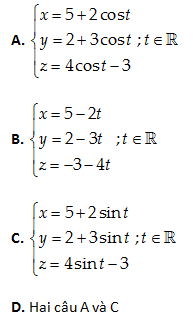
Lời giải:
\left( D \right)//\left( d \right) nên một vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\left( 2,3,4 \right)=-\left( -2,-3,-4 \right)
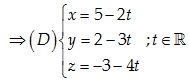
Đáp án cần chọn là: B
Câu 19: Viết phương trình tham số của đường thẳng (D) qua E\left( 2,-4,-2 \right) và vuông góc với mặt phẳng \left( yOz \right).
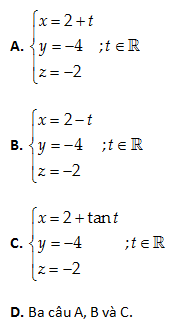
Lời giải:
\left( D \right)\bot \left( yOz \right) nên một vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\overrightarrow{{{e}_{1}}}=\left( 1,0,0 \right)\,\,hay\,\,\overrightarrow{a}=-\left( -1,0,0 \right)
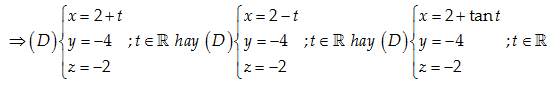
Đáp án cần chọn là: D
Câu 20:
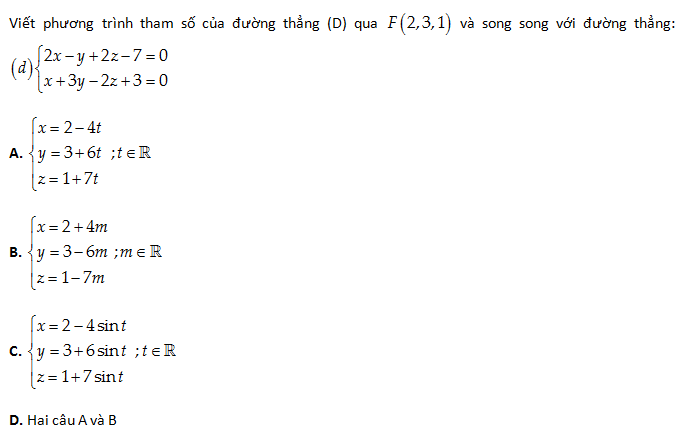
Lời giải:
Hai pháp vectơ của hai mặt phẳng \left( P \right):2x-y+2z-7=0 và \left( Q \right):x+3y-2z+3=0 là \overrightarrow{{{n}_{1}}}=\left( 2,-1,2 \right);\overrightarrow{{{n}_{2}}}=\left( 1,3,-2 \right)
\left( D \right)//\left( d \right) nên vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\left[ \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right]=\left( -4,6,7 \right)=-\left( 4,-6,-7 \right)
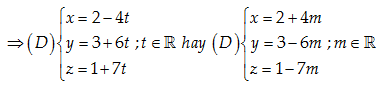
Đáp án cần chọn là: D
Câu 21: Đường thẳng (D):\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z-4}{4} có phương trình tham số là:
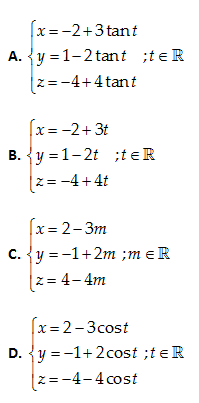
Lời giải:
\left( D \right) qua A\left( 2,-1,4 \right) và có vectơ chỉ phương là \overrightarrow{a}=\left( 3,-2,4 \right)=-\left( -3,2,-4 \right)
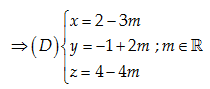
Đáp án cần chọn là: C
Câu 22: Tìm tọa độ giao điểm của hai đường thẳng:
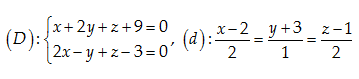
A. \left( 0,4,1 \right)
B. \left( 0,-4,-1 \right)
C. \left( 0,-4,0 \right)
D. \left( 4,1,0 \right)
Lời giải:
\left( d \right):x=2t+2;y=t-3;z=2t+1\left( t\in \mathbb{R} \right)
Thay x,y,z vào x+2y+z+9=0 , ta có:
2t+2+2\left( t-3 \right)+2t+1+9=0\Leftrightarrow t=-1
\Rightarrow Tọa độ giao điểm A của \left( D \right) và\left( d \right):A\left( 0,-4,-1 \right)
Đáp án cần chọn là: B
Câu 23:
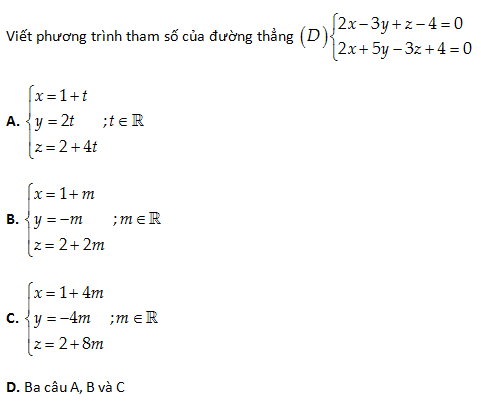
Lời giải:
Hai pháp vectơ của hai mặt phẳng \left( P \right):2x-3y+z-4=0;\,\left( Q \right):2x+5y-3z+4=0 là: \overrightarrow{{{n}_{1}}}=\left( 2,-3,1 \right);\overrightarrow{{{n}_{2}}}=\left( 2,5,-3 \right).
Một vectơ chỉ phương của \left( D \right):\overrightarrow{a}=\left[ \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right]=\left( 4,8,16 \right)\Leftrightarrow \overrightarrow{a}=4\left( 1,2,4 \right)
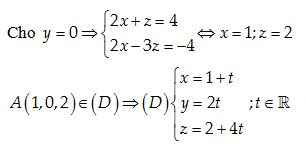
Đáp án cần chọn là: A
Câu 24:
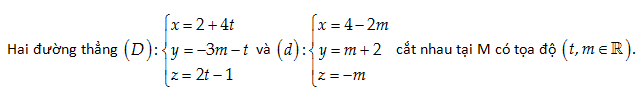
A. \left( 26,9,-11 \right)
B. \left( 26,-9,-11 \right)
C. \left( 26,-9,11 \right)
D. \left( 9,26,-11 \right)
Lời giải:
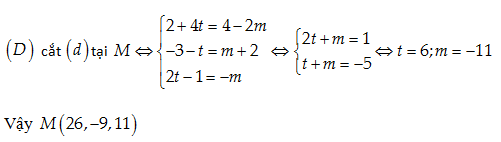
Đáp án cần chọn là: C
Câu 25:
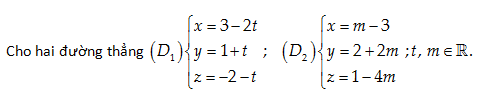
Viết phương trình tổng quát của mặt phẳng \left( P \right) qua \left( {{D}_{1}} \right) và song song với \left( {{D}_{2}} \right).
A. x+7y+5z-20=0
B. 2x+9y+5z-5=0
C. x-7y-5z=0
D. x-7y+5z+20=0
Lời giải:
Hai vectơ chỉ phương của \left( P \right):\overrightarrow{a}=\left( -2,1,-1 \right);\overrightarrow{b}=\left( 1,2,-4 \right)
Pháp vectơ của \left( P \right):\overrightarrow{AN}=\left[ \overrightarrow{a},\overrightarrow{b} \right]=-\left( 2,9,5 \right)
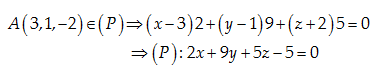
Đáp án cần chọn là: B
Câu 26: Viết phương trình tham số của đường thẳng \left( D \right) qua E\left( 2,-1,-3 \right) và vuông góc với hai đường thẳng \left( {{D}_{1}} \right):\frac{x-1}{3}=y-1=\frac{z+2}{2};\,\,\,\,\,\,\,\,\left( {{D}_{2}} \right):\frac{x}{2}=\frac{y+3}{4}=2-z.
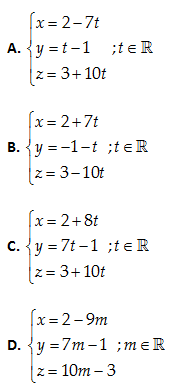
Lời giải:
Hai vectơ chỉ phương của \left( {{D}_{1}} \right) và\left( {{D}_{2}} \right):\overrightarrow{a}=\left( 3,1,2 \right);\overrightarrow{b}=\left( 2,4,-1 \right)
Một vectơ chỉ phương của \left( D \right):\overrightarrow{c}=\left[ \overrightarrow{a},\overrightarrow{b} \right]=\left( -9,7,10 \right)
\Rightarrow \left( D \right):x=2-9t;y=7t-1;z=10t-1;t\in \mathbb{R}
Đáp án cần chọn là: D
Câu 27: Cho tam giác ABC có A\left( 1,2,-3 \right);\,\,B\left( 2,-1,4 \right);\,\,\,C\left( 3,-2,5 \right). Viết phương trình tham số của trung tuyến AM:
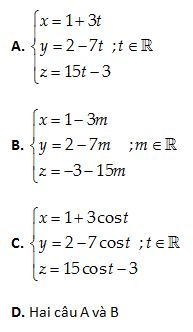
Lời giải:
Trung điểm M của BC: M\left( \frac{5}{2},-\frac{3}{2},\frac{9}{2} \right)
Một vecto chỉ phương của AM: \overrightarrow{AM}=\left( \frac{3}{2},-\frac{7}{2},\frac{15}{2} \right)=\frac{1}{2}\left( 3,-7,15 \right)
\Rightarrow AM:x=1+3t;\,\,y=2-7t;\,\,z=15t-3;\,\,t\in \mathbb{R}
Đáp án cần chọn là: A
Câu 28: Cho tam giác ABC có A\left( 1,2,-3 \right);\,\,B\left( 2,-1,4 \right);\,\,\,C\left( 3,-2,5 \right). Viết phương trình chính tắc của cạnh AB.
A. x-1=\frac{y-2}{-3}=\frac{z+3}{7}
B. x-2=\frac{y+1}{-3}=\frac{z-4}{7}
C. x-1=\frac{2-y}{3}=\frac{z+3}{7}
D. Ba câu A, B và C đúng.
Lời giải:
Một vecto chỉ phương của AB:
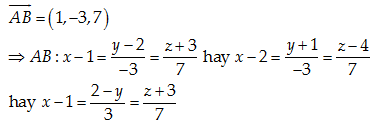
Đáp án cần chọn là: D
Câu 29: Cho tam giác ABC có A\left( 1,2,-3 \right);\,\,B\left( 2,-1,4 \right);\,\,\,C\left( 3,-2,5 \right). Viết phương trình tổng quát của cạnh AC.
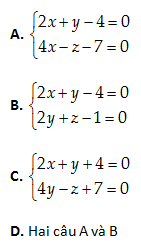
Lời giải:
\overrightarrow{AC}=2\left( 1,-2,4 \right). Phương trình chính tắc của AC:
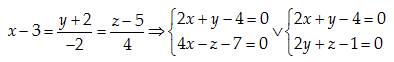
Đáp án cần chọn là: D
Câu 30: Cho tam giác ABC có A\left( 1,2,-3 \right);\,\,B\left( 2,-1,4 \right);\,\,\,C\left( 3,-2,5 \right). Phương trình tổng quát của đường cao AH.
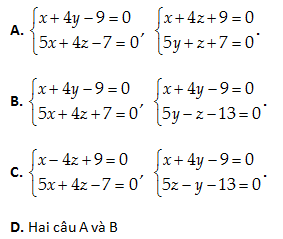
Lời giải:
\overrightarrow{AB}=\left( 1,-3,7 \right);\,\,\overrightarrow{AC}=2\left( 1,-2,4 \right).
Phá vecto của mặt phẳng (ABC):
\overrightarrow{n}=\left[ \overrightarrow{AB},\overrightarrow{AC} \right]=\left( 2,3,1 \right).\,\,\overrightarrow{AH}\bot \overrightarrow{n} và \overrightarrow{AH}\bot \overrightarrow{BC}=\left( 1,-1,1 \right)
\Rightarrow \overrightarrow{AH}=\left[ \overrightarrow{n},\overrightarrow{BC} \right]=\left( 4,-1,-5 \right)
Phương trình chính tắc của AH:\frac{x-1}{4}=\frac{y-2}{-1}=\frac{z+3}{-5}
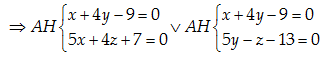
Đáp án cần chọn là: B
Câu 31:
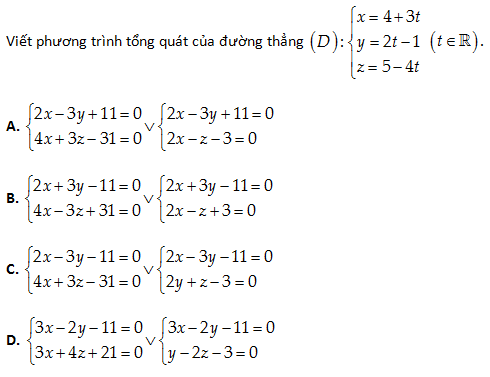
Lời giải:
Phương trình chính tắc của \left( D \right):\frac{x-4}{3}=\frac{y+1}{2}=\frac{z-5}{-4}
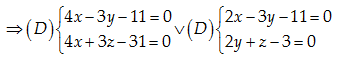
Đáp án cần chọn là: C
Câu 32: Viết phương trình tổng quát của đường thẳng \left( D \right) qua M\left( 4,-2,3 \right) và song song với đường thẳng AB với A\left( -1,2,3 \right);\,\,\,\,B\left( 1,-1,5 \right).
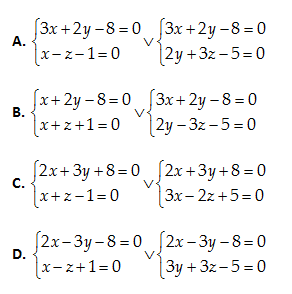
Lời giải:
Một vecto chỉ phương của \left( D \right):\overrightarrow{AB}=\left( 2,-3,2 \right)
Phương trình chính tắc của \left( D \right):\frac{x-4}{2}=\frac{y+2}{-3}=\frac{z-3}{2}
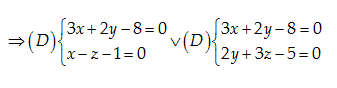
Đáp án cần chọn là: A
Câu 33: Viết phương trình tổng quát của đường thẳng \left( D \right) qua M\left( 3,1,2 \right) và song song với đường thẳng \left( d \right):\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-3}{4}.
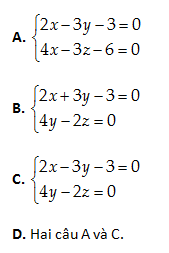
Lời giải:
\left( D \right)//\left( d \right)\Rightarrow Một vecto chỉ phương của \left( D \right):\overrightarrow{a}=\left( 3,2,4 \right)
Phương trình chính tắc của \left( D \right):\frac{x-3}{3}=\frac{y-1}{2}=\frac{z-2}{4}
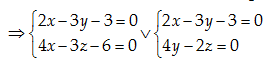
Đáp án cần chọn là: D
Câu 34: Viết phương trình tổng quát của đường thẳng \left( D \right) qua A\left( 2,-2,1 \right) và song song với đường thẳng \left( d \right):x=2-4m;y=3+2m;z=m-5\left( m\in \mathbb{R} \right).
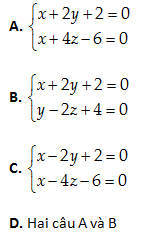
Lời giải:
\left( D \right)//\left( d \right)\Rightarrow Một vecto chỉ phương của \left( D \right):\overrightarrow{a}=\left( -4,2,1 \right)
Phương trình chính tắc của \left( D \right):\frac{x-2}{-4}=\frac{y+2}{2}=z-1
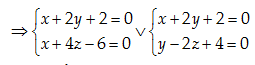
Đáp án cần chọn là: D
Câu 35: Viết phương trình tổng quát của đường thẳng \left( D \right) qua B\left( 2,-3,1 \right) và vuông góc với mặt phẳng \left( yOz \right).
A. y+3=0;z+1=0
B. y+3=0;z-1=0
C. y-3=0;z+1=0
D. y-3=0;z-1=0
Lời giải:
\left( D \right)\bot \left( yOz \right)\Rightarrow \left( D \right)//\left( x'Ox \right).\,\,B92,-3,1\in \left( D \right), nên \left( D \right) là giao tuyến của hai mặt phẳng \left( P \right):y=-3 và \left( Q \right):z=1 qua B và vuông góc với \left( yOz \right).
Đáp án cần chọn là: B
Câu 36: Viết phương trình tổng quát của đường thẳng \left( D \right) qua E\left( 5,2,-3 \right) và vuông góc với trục z'Oz tại H.
A. 2x-5y-25=0;z+3=0
B. 2x+5y=0;z-3=0
C. 2x-5y=0;z+3=0
D. 2x-5y=0;z-3=0
Lời giải:
H\left( 0,0,-3 \right). Một vecto chỉ phương của \left( D \right):\overrightarrow{HE}=\left( 5,2,0 \right)
Phương trình tổng quát của \left( D \right):\frac{x-5}{5}=\frac{y-2}{2};\,\,z=-3
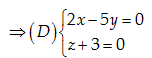
Đáp án cần chọn là: C
Câu 37: Viết phương trình tổng quát của đường thẳng \left( D \right) qua F\left( 3,-4,2 \right) và vuông góc với mặt phẳng \left( P \right):4x-3y+5z-2=0.
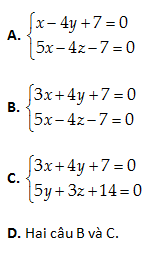
Lời giải:
\left( D \right)\bot \left( P \right)\Rightarrow Một vecto chỉ phương của \left( D \right):\overrightarrow{a}=\left( 4,-3,5 \right)
Phương trình chính tắc của \left( D \right):\frac{x-3}{4}=\frac{y+4}{-3}=\frac{z-2}{5}
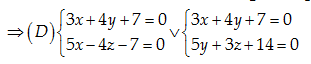
Đáp án cần chọn là: D
Câu 38: Viết phuong trình tổng quát của đường thẳng \left( D \right) qua A\left( 4,2,1 \right) và song song với đường thẳng \left( d \right):x+2y-z=0;x-3y+z-6=0.
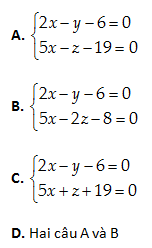
Lời giải:
Hai pháp vecto của hai mặt phẳng: x+2y-z+3=0 và x-3y+z-6=0 là \overrightarrow{{{n}_{1}}}=\left( 1,2,-1 \right);\,\,\overrightarrow{{{n}_{2}}}=\left( 1,-3,1 \right)
Một vecto chỉ phương của \left( d \right):\overrightarrow{a}=\left[ \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right]=-\left( 1,2,5 \right)
Phương trình chính tắc của \left( D \right):x-4=\frac{y-2}{2}=\frac{z-1}{5}
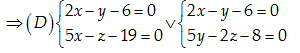
Đáp án cần chọn là: D
Câu 39: Viết phương trình tổng quát của đường thẳng \left( D \right) là giao tuyến của hai mặt phẳng \left( P \right):3x+2y-5z-12=0 và \left( xOy \right).
A. 3x+2y-12=0;z=0
B. 3x+2y+12=0;z=0
C. 2x-3y-12=0;z=0
D. 2x+3y-12=0;z=0
Lời giải:
\left( P \right) cắt Ox và Oy tại A\left( 4,0,0 \right) và B\left( 0,6,0 \right). Moojt vecto chir phuonwg cuar \left( D \right):\overrightarrow{AB}=2\left( -2,3,0 \right)
\Rightarrow \left( P \right):\frac{x-4}{-2}=\frac{y}{3};\,z=0\Leftrightarrow 3x+2y-12=0;\,\,z=0
Đáp án cần chọn là: A
Câu 40: Cho tam giác ABC có A\left( 3,-1,-1 \right);\,\,\,\,B\left( 1,2,-7 \right);\,\,\,\,C\left( -5,14,-3 \right). Viết phương trình của đường phân giác trong BD của góc B.
A. \frac{x-1}{-1}=\frac{y-2}{3}=\frac{z+7}{8}
B. \frac{x-1}{-1}=\frac{y-2}{2}=\frac{z+7}{8}
C. \frac{x-1}{-1}=\frac{y-1}{3}=\frac{z+7}{8}
D. \frac{x-1}{-1}=\frac{y-2}{3}=\frac{z+7}{4}
Lời giải:
\overrightarrow{BA}=\left( 2,-3,6 \right)\Rightarrow BA=7;\overrightarrow{BC}=\left( -6,12,4 \right)\Rightarrow BC=14
\Rightarrow \frac{\overrightarrow{DC}}{\overrightarrow{DA}}=-\frac{BC}{BA}=-2\Rightarrow D chia CA theo tỷ số k=-2
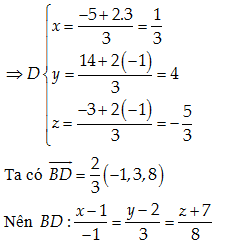
Đáp án cần chọn là: A
Câu 41: Cho tam giác ABC có A\left( 3,-1,-1 \right);\,\,\,\,B\left( 1,2,-7 \right);\,\,\,\,C\left( -5,14,-3 \right). Viết phương trình tổng quát của đường trung trực (d) của cạnh BC của tam giác ABC.
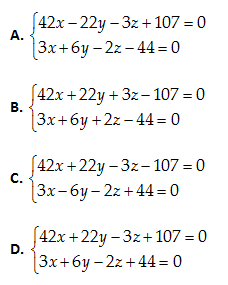
Lời giải:
\overrightarrow{BA}=\left( 2,-3,6 \right),\overrightarrow{BC}=2\left( -3,6,2 \right). Pháp vecto của mặt phẳng \left( ABC \right) là \overrightarrow{n}=\left[ \overrightarrow{BA},\overrightarrow{BC} \right]=-\left( 42,22,-3 \right)
Phương trình \left( ABC \right):\left( x-3 \right)42+\left( y+1 \right)22+\left( z+1 \right)\left( -3 \right)=0
\Leftrightarrow \left( ABC \right):42x+22y-3z-107=0
Trung điểm M của BC: M\left( -2,8,-5 \right)
Phương trình mặt phẳng trung trực \left( P \right) của cạnh BC:
\left( P \right):\,\,\left( x+2 \right)\left( -3 \right)+\left( y-8 \right)6+\left( z+5 \right)2=0
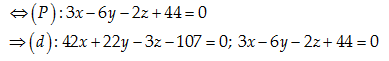
Đáp án cần chọn là: C
Câu 42: Viết phương trình tổng quát của mặt phẳng (P) qua A\left( 1,4,-3 \right) và đường thẳng \left( D \right):x=2-t,\,\,\,y=2t-1,\,\,\,z=1-3t \left( t\in \mathbb{R} \right)
A. 7x+y+3z+12=0
B. 7x-y+3z-12=0
C. 7x+y-3z-12=0
D. 7x-y-3z-12=0
Lời giải:
Một vecto chỉ phương của \left( P \right):\overrightarrow{a}=\left( -1,2,-3 \right);\,B\left( 2,-1,1 \right)\in \left( D \right)
Vecto chỉ phương thứ hai của \left( P \right):\overrightarrow{b}=\overrightarrow{AB}=\left( 1,-5,4 \right)
Một pháp vecto của \left( P \right):\overrightarrow{n}=\left[ \overrightarrow{a},\overrightarrow{b} \right]=\left( -7,1,3 \right)
\Rightarrow \left( P \right):-7\left( x-1 \right)+1\left( y-4 \right)+3\left( z+3 \right)=0\Leftrightarrow 7x-y-3z-12=0
Đáp án cần chọn là: D
Câu 43: Viết phương trình tổng quát của mặt phẳng (P) song song và cách đều hai đường thẳng (D):x=2+3t;\,\,\,y=1-2t;\,\,\,z=2t-1 và \left( d \right):x=t-4;\,\,\,y=3-t;\,\,\,z=3t+1\,\,\,\left( t\in \mathbb{R} \right)
A. 4x-7y+z-10=0
B. 4x-7y+z+10=0
C. 4x+7y-z+10=0
D. 4x+7y+z-10=0
Lời giải:
\left( D \right) qua A\left( 2,1,-1 \right) và vecto chỉ phương \overrightarrow{a}=\left( 3,-2,2 \right)
\left( d \right) qua B\left( -4,3,1 \right) và vecto chỉ phương \overrightarrow{b}=\left( 1,-1,3 \right)
Pháp vecto của \left( P \right):\overrightarrow{n}=\left[ \overrightarrow{a},\overrightarrow{b} \right]=-\left( 4,7,1 \right)
\left( P \right) qua trung điểm MN\left( -1,2,0 \right) của đoạn AB
\Rightarrow \left( P \right):4\left( x+1 \right)+7\left( y-2 \right)+\left( z-0 \right).1=0\Leftrightarrow 4x+7y+z-10=0
Đáp án cần chọn là: D
Câu 44: Viết phương trình tổng quát của mặt phẳng (P) song song và cách đều hai đường thẳng (D):x=2t-1;\,\,\,y=t+2;\,\,\,z=1-3t và \left( d \right):x-y-1=0;\,\,\,z+2=0
A. 3x-3y+z+5=0
B. 6x-6y+2z+7=0
C. 3x-3y+z-5=0
D. 6x-6y+2z-7=0
Lời giải:
\left( D \right) qua M\left( -1,2,1 \right) và có vecto chỉ phương \overrightarrow{a}=\left( 2,1,-3 \right)
Cho y=t\Rightarrow x=t+1;z=-2\Rightarrow \left( d \right):x=t+1;y=t;z=-2
\left( d \right) qua N\left( 1,0,-2 \right) và có vecto chỉ phương \overrightarrow{b}=\left( 1,1,0 \right)
Pháp vecto của \left( P \right):\overrightarrow{n}=\left[ \overrightarrow{a},\overrightarrow{b} \right]=\left( 3,-3,1 \right)
\left( P \right) qua trung điểm E\left( 0,1,-\frac{1}{2} \right) của đoạn MN.
\Rightarrow \left( P \right):\,3\left( x-0 \right)-3\left( y-1 \right)+1\left( z+\frac{1}{2} \right)=0\Leftrightarrow 6x-6y+2z+5=0
Đáp án cần chọn là: B
Câu 45:
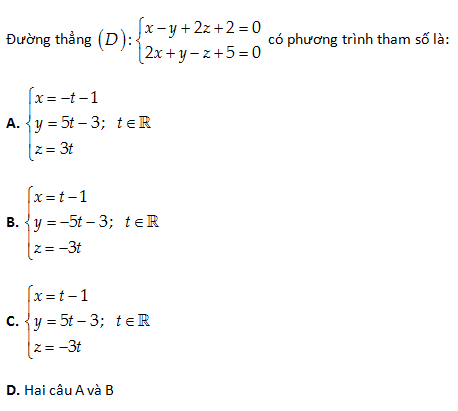
Lời giải:
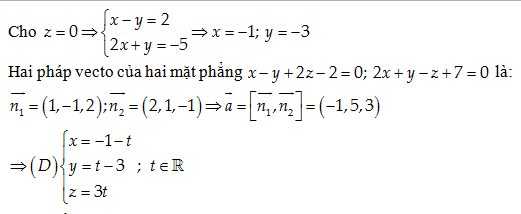
Đáp án cần chọn là: D
Câu 46: Hai đường thẳng \left( D \right):\frac{x-1}{2}=y+3=\frac{z-2}{3};\,\,\,\,\,\left( d \right):\frac{x+2}{3}=\frac{y-1}{2}=\frac{z+4}{4}.
A. Song Song
B. Trùng nhau
C. Chéo nhau
D. Cắt nhau
Lời giải:
A\left( 1,-3,2 \right)\in \left( D \right) và \left( D \right) có vecto chỉ phương \overrightarrow{a}=\left( 2,1,3 \right)
B\left( -2,1,-4 \right)\in \left( d \right) và \left( d \right) có vecto chỉ phương \overrightarrow{b}=\left( 3,2,4 \right)
\overrightarrow{AB}=\left( -3,4,-6 \right)\Rightarrow \left[ \overrightarrow{a},\overrightarrow{b} \right].\overrightarrow{AB}=\left( -2,1,1 \right).\left( -3,4,-6 \right)=4\ne 0
\Rightarrow \left( D \right) và \left( d \right) chéo nhau.
Đáp án cần chọn là: C
Câu 47: Hai dường thẳng \left( D \right):x=2t+3;\,\,y=t+1;\,\,z=3t-2;\,\,\,\,\,\,\left( d \right):x=4t-1;\,\,y=2t-5;\,\,z=6t+1;\,\,t\in \mathbb{R}
A. Song song
B. Chéo nhau
C. Cắt nhau
D. Trùng nhau
Lời giải:
\left( D \right) qua M\left( 3,1,-2 \right) và có vecto chỉ phương \overrightarrow{a}=\left( 2,1,3 \right)
\left( d \right) qua M\left( -1,-5,1 \right) và có vecto chỉ phương \overrightarrow{b}=\left( 4,2,6 \right)=2\left( 2,1,3 \right)
\Rightarrow \overrightarrow{a} và \overrightarrow{b} cùng phương \Rightarrow \left( D \right) và \left( d \right) cùng phương.
\overrightarrow{MN}=\left( -4,-6,3 \right) không cùng phương với \overrightarrow{a}\Rightarrow \left( D \right)//\left( d \right)
Đáp án cần chọn là: A
Câu 48: Hai đường thẳng \left( D \right):x=8t-1;\,\,y=-1-14t;\,\,z=-12t và \left( d \right):x-2y+3z-1=0;\,\,\,2x+2y-z+4=0\,\,\,\left( t\in \mathbb{R} \right)
A. Chéo nhau
B. Cắt nhau
C. Song Song
D. Trùng nhau
Lời giải:
\left( D \right) qua E\left( -1,-1,0 \right) có vecto chỉ phương \overrightarrow{a}=\left( 8,-14,-12 \right)
Hai pháp vecto của hai mặt phẳng x-2y+3z-1=0 và 2x+2y-z+1=0 là \overrightarrow{{{n}_{1}}}=\left( 1,-2,3 \right);\overrightarrow{{{n}_{2}}}=\left( 2,2,-1 \right)
Vecto chỉ phương của \left( d \right):\overrightarrow{b}=\left[ \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \right]=\left( -4,7,6 \right)
Ta có: \frac{8}{-4}=\frac{-14}{7}=\frac{-12}{6}=-2 và tọa độ E\left( -1,-1,0 \right) thỏa man phương trình của \left( d \right)\Rightarrow \left( D \right)\equiv \left( d \right)
Đáp án cần chọn là: D
Câu 49:
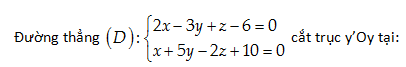
A. \left( 0,2,0 \right)
B. \left( 0,3,0 \right)
C. \left( 0,\frac{6}{5},0 \right)
D. \left( 0,-2,0 \right)
Lời giải:
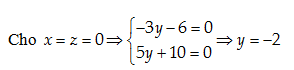
Vậy \left( D \right) cắt y'Oy tại \left( 0,-2,0 \right)
Đáp án cần chọn là: D
Câu 50:
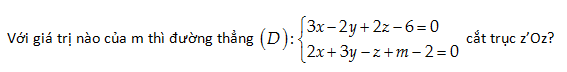
A. -2
B. 5
C. 11
D. 3
Lời giải:
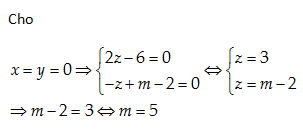
Đáp án cần chọn là: B
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.