Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Số vô tỉ. Căn bậc hai số học sách Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Giải SGK Toán 7 Bài 1 (Cánh diều): Số vô tỉ. Căn bậc hai số học
I. SỐ VÔ TỈ
Hoạt động 1 trang 33 Toán lớp 7 Tập 1: Viết số hữu tỉ dưới dạng số thập phân vô hạn tuần hoàn.
Lời giải:
Ta thực hiện đặt phép tính chia 1 cho 3 như sau:

Sau khi thực hiện phép tính chia 1 cho 3 ta được kết quả là 0,3333….
Vậy số hữu tỉ có thể viết dưới dạng số thập phân vô hạn tuần hoàn là 0, 3333… = 0, (3)
Lời giải:
Phát biểu trên là đúng vì mỗi số vô tỉ đều được viết dưới dạng số thập phân vô hạn không tuần hoàn, còn các số hữu tỉ thì được viết dưới dạng các số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Do vậy nếu một số là vô tỉ thì số đó không thể là số hữu tỉ.
II. CĂN BẬC HAI SỐ HỌC
Hoạt động 2 trang 33 Toán lớp 7 Tập 1: Tính:
a) 32
b) (0,4)^2
Lời giải:
a) 32 = 3.3 = 9
b) (0,4)2 = 0,4.0,4 = 0, 16
Luyện tập 2 trang 34 Toán lớp 7 Tập 1: Tìm giá trị của:
a) √1600
b) √0,16
c) √214
Lời giải:
Ta có:
a) √1600 = √402=40
b) √0,16 = √0,42=0,4
c) √214= √94=√(32)2=32
Hoạt động 3 trang 34 Toán lớp 7 Tập 1:
Lời giải:
Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn, để tính √3;√256.36, ta sử dụng nút dấu căn bậc hai số học √ và làm như sau:

BÀI TẬP
Bài 1 trang 35 Toán lớp 7 Tập 1:
a) Đọc các số sau: √15;√27,6;√0,82.
b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của 911; căn bậc hai số học của 8927.
Lời giải:
a) Đọc số:
√15: Căn bậc hai số học của mười lăm.
√27,6: Căn bậc hai số học của hai mươi bảy phẩy sáu.
√0,82: Căn bậc hai số học của không phẩy tám mươi hai.
b)
Căn bậc hai số học của 39 là √39.
Căn bậc hai số học của 911 là √911
Căn bậc hai số học của 8927 là √8927
Bài 2 trang 35 Toán lớp 7 Tập 1: Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của số 0,64;
b) Số –11 không phải căn bậc hai số học của số 121.
c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng số –1,4 không phải căn bậc hai số học của số 1,96.
Lời giải:
a) Ta có: (0,8)2 = 0,8.0,8 = 0,64 và 0,8 > 0 nên số 0,8 là căn bậc hai số học của số 0,64.
b) Ta có: (–11)2 = (–11).(–11) = 121 nhưng –11 < 0 nên số –11 không là căn bậc hai số học của số 121.
c) Ta có: (1,4)2 = 1,4.1,4 = 1,96 và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96.
(–1,4)2 = (–1,4).(–1,4) = 1,96 nhưng –1,4 < 0 nên số –1,4 không là căn bậc hai số học của số 1,96.
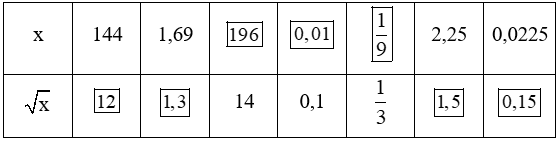
Bài 3 trang 35 Toán lớp 7 Tập 1: Tìm số thích hợp cho ?:

Lời giải:
+) Ta có: 144 = 122 và 12 > 0 nên √x=√144=12.
Khi đó ? điền số 12.
+) Ta có: 1,69 = 1,32 và 1,3 > 0 nên √x=√1,69= 1,3.
Khi đó ? điền số 1,3.
+) Ta có: 142 = 14.14 = 196 nên x = 196.
Khi đó ? điền số 196.
+) Ta có: 0,12 = 0,1.0,1 = 0,01 nên x = 0,01.
Khi đó ? điền số 0,01.
+) Ta có: (13)2=13.13=19 nên x = 19.
Khi đó ? điền số 19.
+) Ta có: 2,25 = 1,52 và 1,5 > 0 nên √x=√2,25=1,5.
Khi đó ? điền số 1,5.
+) Ta có: 0,0225 = 0,152 và 0,15 > 0 nên √x=√0,0225=0,15.
Khi đó ? điền số 0,15.
Ta có bảng sau:
Bài 4 trang 35 Toán lớp 7 Tập 1: Tính giá trị của biểu thức:
a) √0,49+√0,64;
b) √0,36−√0,81;
c) 8.√9−√64
d) 0,1.√400+0,2.√1600
Lời giải:
a)√0,49+√0,64=√0,72+√0,82=0,7+0,8=1,5.
b) √0,36−√0,81=√0,62−√0,92=0,6−0,9=−0,3
c) 8.√9−√64=8.√32−√82=8.3−8=24−8=16
d) 0,1.√400+0,2.√1600=0,1.√202+0,2.√402=0,1.20+0,2.40=2+8=10
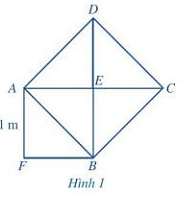
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
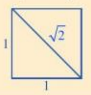
Lưu ý: √2 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1.
Lời giải:
a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB.
Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.
Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (dm2).
Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là: 1 : 2 = 12(dm2).
Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD là: 12.4=2(dm2).
Vậy diện tích hình vuông ABCD là 2 dm2.
b) Do √2 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1, mà hình vuông AEBF có cạnh bằng 1 dm nên đường chéo AB là √2dm.
Vậy độ dài đường chéo AB là √2dm.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.