Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 1: Tập hợp ℚ các số hữu tỉ sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 1  .

Sách bài tập Toán 7 Bài 1 (Cánh diều): Tập hợp ℚ các số hữu tỉ

Bài 1 trang 9 Sách bài tập Toán 7 Tập 1: Các số 0,5; 11; 3,111; $4\frac{5}{7}$; −34; −1,3; $\frac{-1}{-3};\frac{-9}{8}$ có là số hữu tỉ không? Vì sao?

Lời giải:

Ta có $0,5=\frac{1}{2}$ ; $11=\frac{11}{1}$ ; $3,111=\frac{3111}{1000}$ ; $4\frac{5}{7}=\frac{33}{7}$ ; $-34=\frac{-34}{1}$; $-1,3=\frac{-13}{10}$ .

Vì các số $\frac{1}{2}$ ; $\frac{11}{1}$ ; $\frac{3111}{1000}$ ; $\frac{33}{7}$ ; $\frac{-34}{1}$; $\frac{-13}{10}$ ; $\frac{-1}{-3};\frac{-9}{8}$ có dạng $\frac{a}{b}$ , với a, b ∈ ℤ, b ≠ 0.

Nên các số $\frac{1}{2}$ ; $\frac{11}{1}$ ; $\frac{3111}{1000}$ ; $\frac{33}{7}$ ; $\frac{-34}{1}$; $\frac{-13}{10}$ ; $\frac{-1}{-3};\frac{-9}{8}$  là số hữu tỉ.

Vậy các số 0,5; 11; 3,111; $4\frac{5}{7}$; −34; −1,3; $\frac{-1}{-3};\frac{-9}{8}$là số hữu tỉ.

Bài 2 trang 9 Sách bài tập Toán 7 Tập 1: Chọn kí hiệu "∈", "∉" thích hợp cho ?

Lời giải:

∙ Vì −13 là số nguyên âm nên −13 không thuộc tập hợp số tự nhiên.

Do đó ;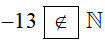

∙ Vì −345 987 là số nguyên âm nên −345 987 thuộc tập hợp số nguyên.

Do đó ;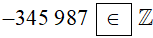

∙ Ta có: $0=\frac{0}{1}$ . Vì 0; 1 ∈ ℤ; 1 ≠ 0 nên $\frac{0}{1}$ là số hữu tỉ hay 0 thuộc tập hợp ℚ.

Do đó ;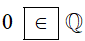

∙ Ta có: $10\frac{34}{75}=\frac{784}{75}$. Vì 784; 75 ∈ ℤ; 75 ≠ 0 nên $\frac{784}{75}$ là số hữu tỉ hay $10\frac{34}{75}$ thuộc tập hợp ℚ.

Do đó ;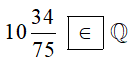

∙ Vì 301 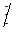 756 nên $\frac{301}{756}$ không thuộc tập hợp số nguyên.

Do đó ;

∙ Vì 13; −499 ∈ ℤ; −499 ≠ 0 nên $\frac{13}{-499}$ là số hữu tỉ hay $\frac{13}{-499}$ thuộc tập hợp ℚ.

Do đó ;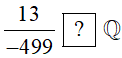

∙ Số −11,01 không phải là số nguyên nên 

∙ Vì −21; −128 ∈ ℤ; −128 ≠ 0 nên $\frac{-21}{-128}$ là số hữu tỉ hay $\frac{-21}{-128}$ thuộc tập hợp ℚ.

Do đó ;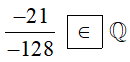

∙ Ta có: $0,3274=\frac{3274}{10000}$. Vì 3 274; 10 000 ∈ ℤ; 10 000 ≠ 0 nên $\frac{3274}{10000}$ là số hữu tỉ hay 0,3274 thuộc tập hợp ℚ.

Do đó ;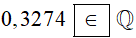

Vậy ta điền vào ô trống như sau:

Bài 3 trang 9 Sách bài tập Toán 7 Tập 1: Trong giờ học nhóm, ba bạn An, Bình, Chi lần lượt phát biểu như sau:

- An: "Số 0 là số nguyên và không phải là số hữu tỉ."

- Bình: "Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ."

- Chi: "Mỗi số nguyên là một số hữu tỉ."

Theo em, bạn nào phát biểu đúng, bạn nào phát biểu sai? Vì sao?

Lời giải:

- An phát biểu sai do 0 viết được dưới dạng phân số $\frac{0}{1}$ nên 0 là số hữu tỉ.

- Bình phát biểu sai do số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ≠ 0.

- Chi phát biểu đúng do mỗi số nguyên a viết được dưới dạng phân số $\frac{a}{1}$.

Bài 4 trang 9 Sách bài tập Toán 7 Tập 1: Quan sát trục số ở Hình 5, điểm nào biểu diễn số hữu tỉ $\frac{3}{4}$ ?

Lời giải:

Ta thấy: $\frac{3}{4}$ là số hữu tỉ dương và $0<\frac{3}{4}<1$ .

Ta chia đoạn thẳng đơn vị thành 4 phần bằng nhau, lấy một đoạn làm đơn vị mới.

Khi đó, điểm biểu diễn số hữu tỉ $\frac{3}{4}$ là điểm nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 3 lần đơn vị mới.

Do đó điểm C biểu diễn số hữu tỉ $\frac{3}{4}$.

Vậy trên trục số ở Hình 5, điểm C biểu diễn số hữu tỉ $\frac{3}{4}$ .

Bài 5 trang 9 Sách bài tập Toán 7 Tập 1: Tìm số đối của mỗi số hữu tỉ sau: $\frac{37}{221}$; $\frac{-93}{1171}$; $\frac{87}{-19543}$; 41,02; −791,8.

Lời giải:

Số đối của $\frac{37}{221}$  là $-\frac{37}{221}$ ;

Số đối của $\frac{-93}{1171}$  là $-\left(\frac{-93}{1171}\right)=\frac{93}{1171}$ ;

Số đối của $\frac{87}{-19543}$  là $-\left(\frac{87}{-19543}\right)=\frac{87}{19543}$ ;

Số đối của 41,02 là −41,02;

Số đối của −791,8 là 791,8.

Vậy số đối của các số $\frac{37}{221}$ ; $\frac{-93}{1171}$ ; $\frac{87}{-19543}$ ; 41,02; −791,8 lần lượt là $-\frac{37}{221}$ ; $\frac{93}{1171}$ ; $\frac{87}{19543}$ ; −41,02; 791,8.

Bài 6 trang 9 Sách bài tập Toán 7 Tập 1: Biểu diễn số đối của mỗi số hữu tỉ đã cho trên trục số ở Hình 6.

Lời giải:

Số đối của các số $\frac{-9}{4}$ ; $\frac{-7}{4}$ ; −1; $\frac{-1}{2}$ ; 0; 1; $\frac{5}{4}$  lần lượt là $\frac{9}{4}$ ; $\frac{7}{4}$ ; 1; ; 0; −1; $\frac{-5}{4}$ .

Ta có: $\frac{1}{2}=\frac{2}{4}$ .

Chia đoạn thẳng đơn vị thành 4 đoạn thẳng bằng nhau, ta được đơn vị mới bằng $\frac{1}{4}$  đơn vị cũ.

∙ Số hữu tỉ $\frac{9}{4}$  nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 9 đơn vị mới.

∙ Số hữu tỉ $\frac{7}{4}$  nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 7 đơn vị mới.

∙ Số hữu tỉ $\frac{1}{2}$  hay số hữu tỉ $\frac{2}{4}$ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 2 đơn vị mới.

∙ Số hữu tỉ $\frac{-5}{4}$ nằm bên trái điểm 0 và cách điểm 0 một khoảng bằng 5 đơn vị mới.

Vậy biểu diễn số đối của các số $\frac{-9}{4}$ ; $\frac{-7}{4}$ ; −1; $\frac{-1}{2}$ ; 0; 1; $\frac{5}{4}$  trên trục số như sau:

Bài 7 trang 10 Sách bài tập Toán 7 Tập 1: So sánh:

a) $3\frac{2}{11}$  và 3,2;

b) $\frac{-5}{211}$  và −0,01;

c) $\frac{105}{-15}$  và −7,112;

d) −943,001 và 943,0001.

Lời giải:

a) $3\frac{2}{11}$ và 3,2

Ta có: $3\frac{2}{11}=\frac{35}{11}=\frac{175}{55}$ ; $3,2=\frac{16}{5}=\frac{176}{55}$ .

Vì 175 < 176 nên $\frac{175}{55}<\frac{176}{55}$  hay $3\frac{2}{11}<3,2$ .

Vậy $3\frac{2}{11}<3,2$ .

b) $\frac{-5}{211}$  và −0,01

Ta có $-0,01=\frac{-1}{100}=\frac{-5}{500}$ .

Vì 211 < 500 nên $\frac{5}{211}>\frac{5}{500}$

Suy ra $\frac{-5}{211}<\frac{-5}{500}$  hay $\frac{-5}{211}<-0,01$ .

Vậy $\frac{-5}{211}<-0,01$ .

c) $\frac{105}{-15}$  và −7,112

Ta có: $\frac{105}{-15}=-7$ .

Số đối của −7 và −7,112 lần lượt là 7 và 7,112.

Vì 7 < 7,112 nên −7 > −7,112.

Vậy −7 > −7,112.

d) −943,001 và 943,0001.

Ta có: −943,001 < 0 và 943,0001 > 0.

Vậy −943,001 < 943,0001.

Bài 8 trang 10 Sách bài tập Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự tăng dần:

a) $3\frac{2}{11};2\frac{1}{12};\frac{15}{21};\frac{17}{21}$ ;

b) −5,12; 0,534; −23; 123; 0; 0,543.

Lời giải:

a) Ta có $3\frac{2}{11}>1;2\frac{1}{12}>1$ ; $\frac{15}{21}<1;\frac{17}{21}<1$.

∙ Nhóm các số lớn hơn 1: $3\frac{2}{11};2\frac{1}{12}$ .

Ta thấy hai hỗn số $3\frac{2}{11};2\frac{1}{12}$  có phần nguyên 2 < 3 nên $2\frac{1}{12}<3\frac{2}{11}$ .

∙ Nhóm các số nhỏ hơn 1: $\frac{15}{21};\frac{17}{21}$.

Vì 15 < 17 nên $\frac{15}{21}<\frac{17}{21}$ .

Do đó $\frac{15}{21}<\frac{17}{21}<2\frac{1}{12}<3\frac{2}{11}$ .

Vậy các số sau theo thứ tự tăng dần là $\frac{15}{21};\frac{17}{21};2\frac{1}{12};3\frac{2}{11}$ .

b) ∙ Nhóm các số dương: 0,534; 123; 0,543.

Ta có: 0,534 < 0,543 < 123.

∙ Nhóm các số âm: −5,12; −23.

Ta có: −23 < −5,12.

Do đó −23 < −5,12 < 0 < 0,534 < 0,543 < 123.

Vậy các số được sắp xếp theo thứ tự tăng dần: −23; −5,12; 0; 0,534; 0,543; 123.

Bài 9 trang 10 Sách bài tập Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự giảm dần:

a) $\frac{2}{15};\frac{2}{3};-\frac{7}{8};\frac{5}{6};\frac{-7}{9}$ ;

b) $\frac{19}{22};0,5;-\frac{1}{4};-0,05;2\frac{1}{6}$ .

Lời giải:

a) ∙ Nhóm các phân số dương: $\frac{2}{15};\frac{2}{3};\frac{5}{6}$ .

Ta có: $\frac{2}{15}=\frac{4}{30};\frac{2}{3}=\frac{20}{30};\frac{5}{6}=\frac{25}{30}$ .

Vì 25 > 20 > 4 nên $\frac{25}{30}>\frac{20}{30}>\frac{4}{30}$ .

Suy ra $\frac{5}{6}>\frac{2}{3}>\frac{2}{15}$ .

∙ Nhóm các phân số âm: $-\frac{7}{8};\frac{-7}{9}$ .

Ta có: $-\frac{7}{8}=\frac{-63}{72};\frac{-7}{9}=\frac{-56}{72}$ .

Vì −56 > −63 nên $\frac{-56}{72}>\frac{-63}{72}$  hay $\frac{-7}{9}>-\frac{7}{8}$ .

Do đó $\frac{5}{6}>\frac{2}{3}>\frac{2}{15}>\frac{-7}{9}>-\frac{7}{8}$ .

Vậy các số được sắp xếp theo thứ tự giảm dần: $\frac{5}{6};\frac{2}{3};\frac{2}{15};\frac{-7}{9};-\frac{7}{8}$ .

b) ∙ Nhóm các số dương: $\frac{19}{22};0,5;2\frac{1}{6}$ .

Ta thấy: $2\frac{1}{6}>1$ (vì hỗn số $2\frac{1}{6}$ có phần nguyên 2 > 1).

$\frac{19}{22}<1$ (phân số có tử số bé hơn mẫu số); 0,5 < 1.

Ta có: $0,5=\frac{1}{2}=\frac{11}{22}$ .

Vì 19 < 11 nên $\frac{19}{22}>\frac{11}{22}$  hay $\frac{19}{22}>0,5$ .

Do đó $2\frac{1}{6}>\frac{19}{22}>0,5$ .      (1)

∙ Nhóm các số âm: $-\frac{1}{4};-0,05$ .

Ta có: $-\frac{1}{4}=-0,25$ .

Vì −0,05 > −0,25 nên $-0,05>-\frac{1}{4}$ .     (2)    

Từ (1) và (2) suy ra: $2\frac{1}{6}>\frac{19}{22}>0,5>-0,05>-\frac{1}{4}$ .

Vậy các số được sắp xếp theo thứ tự giảm dần: $2\frac{1}{6};\frac{19}{22};0,5;-0,05;-\frac{1}{4}$ .

Bài 10 trang 10 Sách bài tập Toán 7 Tập 1: Cho số hữu tỉ $y=\frac{2a-4}{3}$  (a là số nguyên). Với giá trị nào của a thì:

a) y là số nguyên?

b) y không là số hữu tỉ âm và cũng không là số hữu tỉ dương?

Lời giải:

a) Ta có: 2a – 4 = 2(a – 2).

Với y là số nguyên thì (2a – 4) ⋮ 3 hay 2(a – 2) ⋮ 3.

Vì ƯCLN(2, 3) = 1 nên (a – 2) ⋮ 3 hay a – 2 = 3k (k ∈ ℤ).

Suy ra a = 3k + 2.

Vậy a là số chia 3 dư 2.

b) Với y không là số hữu tỉ âm và cũng không là số hữu tỉ dương nên y = 0.

Suy ra 2a – 4 = 0 hay a = 2.

Vậy a = 2.