Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 47, 48, 49, 50, 51, 52, 53 Bài 4: Bất phương trình bậc nhất một ẩn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 47, 48, 49, 50, 51, 52, 53 Bài 4: Bất phương trình bậc nhất một ẩn
Câu hỏi Vở bài tập Toán 8 trang 47 - 53:
Câu 9.
Khoanh tròn vào chữ cái trước khẳng định đúng. Bất phương trình tương đương với các bất phương trình:
Phương pháp giải:
Sử dụng: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
Giải chi tiết:
Ta có:
Vậy tập nghiệm của bất phương trình là .
Vậy tập nghiệm của bất phương trình là .
Vậy tập nghiệm của bất phương trình là .
Do đó phương trình và có cùng tập nghiệm là nên hai phương trình này tương đương.
Chọn D.
Câu 10.
Khoanh tròn vào chữ cái trước khẳng định đúng. Bất phương trình bậc nhất có tập nghiệm biểu diễn bởi hình vẽ sau:

Phương pháp giải:
Tìm tập nghiệm của bất phương trình từ đó chọn hình vẽ biểu diễn tập nghiệm đó.
Giải chi tiết:
Biểu diễn tập nghiệm trên trục số như sau:
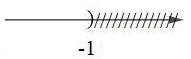
Chọn B
Vở bài tập Toán 8 trang 47 - 53 Bài 13: Giải các bất phương trình (theo quy tắc chuyển vế):
a, x - 5 > 3
b, x - 2 < - 2x + 4
c, - 3x >- 4x + 2
d, 8x + 2 < 7x - 1Phương pháp giải:
a, Áp dụng qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
b, Áp dụng qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
c, Áp dụng qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
d, Áp dụng qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
Lời giải:
a,
Ta có
.
Vậy nghiệm của bất phương trình đã cho là .
b,
Ta có:
.
Vậy nghiệm của bất phương trình đã cho là .
c,
Ta có
Vậy nghiệm của bất phương trình đã cho là .
d,
Ta có
Vậy nghiệm của bất phương trình đã cho là .Vở bài tập Toán 8 trang 47 - 53 Bài 14: Giải các bất phương trình sau (theo quy tắc nhân)
a, 0,3x > 0,6
b, -4x < 12
c, - x > 4
d, 1,5x > - 9
Phương pháp giải:
a,
Áp dụng qui tắc nhân với một số:
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
b,
Áp dụng qui tắc nhân với một số:
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
c,
Áp dụng qui tắc nhân với một số:
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm
d,
Áp dụng qui tắc nhân với một số:
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
Lời giải:
a,
Ta có
Vậy nghiệm của bất phương trình đã cho là:
b,
Ta có
Vậy nghiệm của bất phương trình đã cho là:
c,
Ta có
Vậy nghiệm của bất phương trình đã cho là:
d,
Ta có
Vậy nghiệm của bất phương trình đã cho là:
Vở bài tập Toán 8 trang 47 - 53 Bài 15: Giải thích sự tương đương sau:
a, x - 3 > 1 ⇔ x + 3 > 7
b, - x < 2 ⇔ 3x > - 6
Phương pháp giải:
a, Áp dụng định nghĩa hai bất phương trình tương đương: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
b, Áp dụng định nghĩa hai bất phương trình tương đương: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
Lời giải:
a,
Ta có
Ta có
Hai bất phương trình và có cùng tập nghiệm nên tư
b,
Nhân cả hai vế của bất phương trình với số và bất đẳng thức đổi chiều, ta được .
Vậy hai bất phương trình và tương đương.
Vở bài tập Toán 8 trang 47 - 53 Bài 16: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a, 2x - 3 > 0
b, 3x + 4 < 0
c, 4 - 3x ≤ 0
d, 5 - 2x ≥ 0
Phương pháp giải:
a,
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
b,
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
c,
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
d,
Áp dụng
- Qui tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm
Lời giải:
a,
Ta có
Vậy nghiệm của bất phương trình là và được biểu diễn trên trục số như sau:

b,
Ta có
Vậy nghiệm của bất phương trình là và được biểu diễn trên trục số như sau:

c,
Ta có
Vậy nghiệm của bất phương trình là và được biểu diễn trên trục số như sau:

d,
Ta có
Vậy nghiệm của bất phương trình là và được biểu diễn trên trục số như sau:
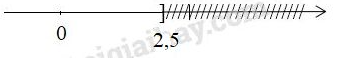
Vở bài tập Toán 8 trang 47 - 53 Bài 17: Giải các bất phương trình:
a,
b,
c, 3 >2
d, 5 >2
Phương pháp giải:
a, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.
b, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.
c, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số
d, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số
Lời giải:
a,
Ta có
Vậy nghiệm của bất phương trình là .
b,
Ta có
Vậy nghiệm của bất phương trình là .
c,
Ta có
Vậy nghiệm của bất phương trình là .
d,
Ta có
Vậy nghiệm của bất phương trình là .
Vở bài tập Toán 8 trang 47 - 53 Bài 18: Đố. Kiểm tra xem giá trị có là nghiệm của bất phương trình sau không:
a,
b, (- 0,001)x > 0,003
Phương pháp giải:
a, Bước 1: Giải tìm tập nghiệm của bất phương trình
Bước 2: Thay giá trị vào tập nghiệm của bất phương trình:
+) Nếu cho khẳng định đúng thì là nghiệm của bất phương trình
+) Nếu cho khẳng định sai thì không là nghiệm của bất phương trình.
b,
Bước 1: Giải tìm tập nghiệm của bất phương trình
Bước 2: Thay giá trị vào tập nghiệm của bất phương trình:
+) Nếu cho khẳng định đúng thì là nghiệm của bất phương trình
+) Nếu cho khẳng định sai thì không là nghiệm của bất phương trình
Lời giải:
a,
Ta có
Ta thấy là nghiệm của nên là nghiệm của
b,
Ta có
Ta thấy không phải là nghiệm của bất phương trình nên cũng không phải là nghiệm của bất phương trình .
Vở bài tập Toán 8 trang 47 - 53 Bài 19: Tìm x sao cho
a, Giá trị của biểu thức 2x - 5 không âm
b, Giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5.
Phương pháp giải:
a, Chú ý:
- không âm tức là
b,
- không lớn hơn tức là
- Dựa vào dữ kiện của bài lập bất phương trình sau đó giải bất phương trình để tìm tập nghiệm
Lời giải:
a,
Tìm sao cho giá trị của biểu thức không âm nghĩa là giải bất phương trình
Ta có
Vậy để không âm thì .
b,
Tìm sao cho giá trị của biểu thức không lớn hơn giá trị của biểu thức nghĩa là giải bất phương trình
Ta có
Vậy giá trị của phải tìm là
Vở bài tập Toán 8 trang 47 - 53 Bài 20: Một người có số tiền không quá đồng gồm tờ giấy bạc với hai loại mệnh giá: loại đồng và loại đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại đồng?
Phương pháp giải:
Bước 1: Đặt số tờ giấy bạc loại đồng làm ẩn, sau đó biểu diễn đại lượng còn lại theo ẩn.
Bước 2: Dựa vào đề bài ta lập được bất phương trình.
Bước 3: Giải bất phương trình.
Bước 4: Kết luận
Lời giải:
Gọi số tờ giấy bạc loại đồng là ( nguyên dương) thì số tờ giấy bạc loại đồng là .
Từ đó, ta có số tiền tương ứng với số giấy bạc loại đồng và là và đồng.
Theo bài ra, tổng số tiền không quá đồng nên ta có bất phương trình:
Ta có:
Do là số nguyên dương, nên có thể là các số nguyên từ đến .
Vậy số tờ giấy bạc loại đồng có thể là tờ, tờ ... và tối đa là tờ
Vở bài tập Toán 8 trang 47 - 53 Bài 21: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a, > 5
b, <13
c,
d,
Phương pháp giải:
a, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số
b, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số
c, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.
d, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.
Lời giải:
a,
Ta có
Vậy nghiệm là và được biểu diễn trên trục số như sau:

b,
Ta có
Vậy nghiệm là và được biểu diễn trên trục số như sau:
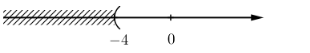
c,
Ta có
Vậy nghiệm là và được biểu diễn trên trục số như sau:

d,
Ta có
Vậy nghiệm là và được biểu diễn trên trục số như sau:

Vở bài tập Toán 8 trang 47 - 53 Bài 22: Giải các bất phương trình:
a, 8x + 3(x + 1) > 5x - (2x - 6)b, 2x(6x - 1) > (3x - 2) (4x + 3)
Phương pháp giải:
a, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.
b, Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.Lời giải:
a,
Vậy nghiệm là
b,
Vậy nghiệm là

