Phương pháp giải:

a, Áp dụng định nghĩa nghiệm của bất phương trình: Nghiệm của bất phương trình là giá trị của ẩn thay vào bất phương trình ta được một khẳng định đúng.

Thay $x=-2$ vào bất phương trình: $-3x+2>-5$, ta được khẳng định $-3.(-2)+2>-5$

Ta tính $-3.(-2)+2=6+2=8$

Ta có $8>-5$, nên khẳng định $-3.(-2)+2>-5$ là đúng.

Vậy $x=-2$ là nghiệm của bất phương trình $-3x+2>-5$.

Thay $x=-2$ vào bất phương trình: $10-2x<2$, ta được khẳng định $10-2.(-2)<2$

Ta tính $10-2.(-2)=10+4=14$

Ta có $14>2$, nên khẳng định $10-2.(-2)<2$ là sai. 

Vậy $x=-2$ không là nghiệm của bất phương trình $10-2x<2$.

Thay $x=-2$ vào bất phương trình $x^2-5<1$, ta được khẳng định ${\left(-2\right)}^2-5<1$

Ta tính ${\left(-2\right)}^2-5=4-5=-1$ 

Ta có $-1<1$ nên khẳng định ${\left(-2\right)}^2-5<1$ là đúng.

Vậy $x=-2$ là nghiệm của bất phương trình $x^2-5<1$

Thay $x=-2$ vào bất phương trình $|x|<3$, ta được khẳng định $|-2|<3$

Ta có $|-2|=2$ mà $2<3$, nên khẳng định $|-2|<3$ là đúng.

Vậy $x=-2$ là nghiệm của bất phương trình $|x|<3$. 

Thay $x=-2$ vào bất phương trình $|x|>2$, ta được khẳng định $|-2|>2$

Ta có $|-2|=2$ nên khẳng định $|-2|>2$ là sai. 

Vậy $x=-2$ không là nghiệm của bất phương trình $|x|>2$.

Thay $x=-2$ vào bất phương trình $x+1>7-2x$, ta được khẳng định

$(-2)+1>7–2.(-2)$

Ta tính $(-2)+1=-1$

           $7–2.(-2)=7-(-4)=11$

Ta có $-1<11$ nên khẳng định $(-2)+1>7–2.(-2)$ là sai.

Vậy $x=-2$ không là nghiệm của bất phương trình $x+1>7-2x$.

Phương pháp giải:

a, Áp dụng quy tắc chuyển vế, quy tắc nhân với một số

b, Áp dụng quy tắc chuyển vế, quy tắc nhân với một số

Ta có  ${\displaystyle \frac{2-x}{4}}<5$

$\begin{array}{l}\iff 2-x<20\\ \iff -x<20-2\\ \iff x>-18\end{array}$  

Vậy nghiệm là $x>-18$. 

Ta có

$3⩽{\displaystyle \frac{2x+3}{5}}$

$\iff 15\le 2x+3$

$\iff 12\le 2x$

$\iff 6\le x$

Vậy nghiệm là $x\ge 6$ 

Ta có

${\displaystyle \frac{4x-5}{3}}>{\displaystyle \frac{7-x}{5}}$ 

$\iff 20x–25>21–3x$

$\iff 23x>46$    

$\iff x>2$

Vậy nghiệm là $x>2$ 

Ta có

${\displaystyle \frac{2x+3}{-4}}⩾{\displaystyle \frac{4-x}{-3}}$

$\iff 6x+9\le 16–4x$

$\iff 10x\le 7$

$\iff x\le {\displaystyle \frac{7}{10}}$

Vậy nghiệm là $x\le {\displaystyle \frac{7}{10}}$ 

a,Tìm $x$ sao cho giá trị của biểu thức $5-2x$ là số dương nghĩa là giải bất phương trình $5–2x>0$

Ta có $5–2x>0$

$\iff 5>2x$

$\iff {\displaystyle \frac{5}{2}}>x$

$\iff x<{\displaystyle \frac{5}{2}}$

Vậy giá trị $x$ phải tìm là $x<{\displaystyle \frac{5}{2}}$.

Tìm $x$ sao cho giá trị của biểu thức $x+3$ nhỏ hơn giá trị của biểu thức $4x-5$ nghía là giải bất phương trình $x+3<4x-5$.

Ta có $x+3<4x-5$

$\iff x-4x<-5-3$

$\iff x>{\displaystyle \frac{8}{3}}$

Vậy giá trị $x$ phải tìm là $x>{\displaystyle \frac{8}{3}}$.

c,

Tìm $x$ sao cho giá trị của biểu thức $2x+1$ không nhỏ hơn giá trị của biểu thức $x+3$ nghĩa là giải bất phương trình $2x+1\ge x+3$

Ta có $2x+1\ge x+3$

$\iff x\ge 2$ 

Vậy giá trị $x$ phải tìm là $x\ge 2$.

d,

Tìm $x$ sao cho giá trị của biểu thức $x^2+1$ không lớn hơn giá trị của biểu thức ${\left(x-2\right)}^2$ nghĩa là giải bất phương trình $x^2+1⩽{\left(x-2\right)}^2$.

Ta có $x^2+1⩽{\left(x-2\right)}^2$

$\begin{array}{rl}& \iff x^2+1\le x^2-4x+4\\ & \iff 4x\le 3\\ & \iff x\le \frac{3}{4}\end{array}$

Vậy giá trị $x$ phải tìm là $x⩽{\displaystyle \frac{3}{4}}$ 

$A(x)=B(x)$ với $A(x)\ge 0$

hoặc $-A(x)=B(x)$ với $A(x)<0$

b, Áp dụng cách giải của dạng toán: $|A(x)|=B(x)$

$A(x)=B(x)$ với $A(x)\ge 0$

hoặc $-A(x)=B(x)$ với $A(x)<0$

c, Áp dụng cách giải của dạng toán: $|A(x)|=B(x)$

$A(x)=B(x)$ với $A(x)\ge 0$

hoặc $-A(x)=B(x)$ với $A(x)<0$

d, Áp dụng cách giải của dạng toán: $|A(x)|=B(x)$

$A(x)=B(x)$ với $A(x)\ge 0$

hoặc $-A(x)=B(x)$ với $A(x)<0$

Lời giải:

a, Áp dụng cách giải của dạng toán: 

$|3x|=x+8$

Ta có $|3x|=3x$ khi $3x\ge 0$ hay $x\ge 0$

         $|3x|=-3x$ khi $3x<0$ hay $x<0$

+ Ta giải $3x=x+8$ với điều kiện $x\ge 0$ 

Ta có $3x=x+8$

$\iff 2x=8$

$\iff x=4$

Giá trị $x=4$ là nghiệm vì thỏa mãn điều kiện $x\ge 0$.

+ Ta giải $-3x=x+8$ với điều kiện $x<0$

Ta có $-3x=x+8$

$\iff -4x=8$

$\iff x=-2$

Giá trị $x=-2$ là nghiệm vì thỏa mãn điều kiện $x<0$.

Vậy phương trình $|3x|=x+8$ có tập nghiệm là $S=\{4;-2\}$.

b,

Ta có $|-2x|=-2x$ khi $-2x\ge 0$ hay $x\le 0$

        $|-2x|=2x$ khi $-2x<0$ hay $x>0$

+ Ta giải $-2x=4x+18$ với điều kiện $x\le 0$ 

$\iff -6x=18$

$\iff x=-3$

Giá trị $x=-3$ là nghiệm vì đã thỏa mãn điều kiện $x\le 0$.

+ Ta giải $2x=4x+18$ với điều kiện $x>0$.

$\iff -2x=18$

$\iff x=-9$

Giá trị $x=-9$ bị loại vì không thỏa mãn điều kiện $x>0$.

Vậy phương trình $|-2x|=4x+18$  chỉ có một nghiệm $x=-3$.

c,

Ta có $|x-5|=x-5$ khi $x-5\ge 0$ hay $x\ge 5$.

         $|x-5|=-x+5$ khi $x-5<0$ hay $x<5$.

+ Ta giải $x-5=3x$ với điều kiện $x\ge 5$.

Ta có $x-5=3x$

$\iff -2x=5$

$\iff x=-{\displaystyle \frac{5}{2}}$

Giá trị $x=-{\displaystyle \frac{5}{2}}$ bị loại vì không thỏa mãn điều kiện $x\ge 5$.

+ Ta giải $-x+5=3x$ với điều kiện $x<5$. 

Ta có $-x+5=3x$

$\iff -4x=-5$

$\iff x={\displaystyle \frac{5}{4}}$

Giá trị $x={\displaystyle \frac{5}{4}}$ là nghiệm vì đã thỏa mãn điều kiện $x<5$.

Vậy phương trình  chỉ có một nghiệm là $x =\frac{5}{4}$ .

d,

Ta có $|x+2|=x+2$ khi $x+2\ge 0$ hay $x\ge -2$

         $|x+2|=-x-2$ khi $x+2<0$ hay $x<-2$

+ Ta giải $x+2=2x-10$ với điều kiện $x\ge -2$

Ta có $x+2=2x-10$

$\iff -x=-12$

$\iff x=12$

Giá trị $x=12$ là nghiệm vì đã thỏa mãn điều kiện $x\ge -2$.

+ Ta giải $-x-2=2x-10$ với điều kiện $x<-2$

Ta có $-x-2=2x-10$

$\iff -3x=-8$

$\iff x={\displaystyle \frac{8}{3}}$ 

Giá trị $x={\displaystyle \frac{8}{3}}$ bị loại vì không thỏa mãn điều kiện $x<-2$

Vậy phương trình $|x+2|=2x–10$ chỉ có một nghiệm là $x=12$. 

Câu 1. (1,5 điểm). Hãy chọn khẳng định đúng. Cho $a>b$, ta có:

(A) $-2a>-2b$

(B) $a+3<b+3$

(C) $3-2a<3-2b$

(D) $3+2a<3+2b$

Câu 2. (1,5 điểm). Hãy chọn khẳng định đúng. Bất phương trình $3x-2\le 0$ có tập nghiệm biểu diễn bởi hình vẽ sau:

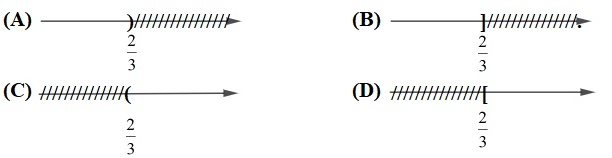
Câu 3. (2,0 điểm). Giải bất phương trình $-2x+6\le 0$ và biểu diễn tập nghiệm trên trục số.

Câu 4. (3,0 điểm). Tìm $x$ sao cho:

a) Giá trị của biểu thức $3-4x$ lớn hơn giá trị của biểu thức $2(3-x)$.

b) Giá trị của biểu thức ${\displaystyle \frac{3x-1}{2}}$ không lớn hơn giá trị của biểu thức $x+2$.

Câu 5. (2,0 điểm). Giải phương trình $|x+4|=3x-5$.

Câu 1:

Phương pháp:

Sử dụng:

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

- Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Lời giải:

$\begin{array}{l}a>b\\ \iff -2a<-2b\\ \iff 3-2a<3-2b\end{array}$

Chọn C.

Câu 2:

Phương pháp:

- Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác $0$ để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

$\begin{array}{l}3x-2\le 0\\ \iff 3x\le 2\\ \iff x\le {\displaystyle \frac{2}{3}}\end{array}$

Vậy phương trình có nghiệm là $x\le {\displaystyle \frac{2}{3}}$.

Biểu diễn tập nghiệm trên trục số như sau

Câu 3:

Phương pháp:

- Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác $0$ để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

$\begin{array}{l}-2x+6\le 0\\ \iff -2x\le -6\\ \iff x\ge \left(-6\right):\left(-2\right)\\ \iff x\ge 3\end{array}$

Vậy nghiệm của bất phương trình là: $x\ge 3$.

Biểu diễn tập nghiệm trên trục số như sau:

Câu 4:

Phương pháp:

a) Giá trị của biểu thức $3-4x$ lớn hơn giá trị của biểu thức $2(3-x)$ tức là ta đi giải phương trình $3-4x>2\left(3-x\right)$

Giá trị của biểu thức ${\displaystyle \frac{3x-1}{2}}$ không lớn hơn giá trị của biểu thức $x+2$ tức là ta đi giải phương trình ${\displaystyle \frac{3x-1}{2}}\le x+2$.

Lời giải:

a) Giá trị của biểu thức $3-4x$ lớn hơn giá trị của biểu thức $2(3-x)$ tức là ta đi giải phương trình $3-4x>2\left(3-x\right)$

$\begin{array}{l}3-4x>2\left(3-x\right)\\ \iff 3-4x>6-2x\\ \iff -4x+2x>6-3\\ \iff -2x>3\\ \iff x<{\displaystyle \frac{3}{2}}\end{array}$

Vậy $x<{\displaystyle \frac{3}{2}}$ thì giá trị của biểu thức $3-4x$ lớn hơn giá trị của biểu thức $2(3-x)$.

b) Giá trị của biểu thức ${\displaystyle \frac{3x-1}{2}}$ không lớn hơn giá trị của biểu thức $x+2$ tức là ta đi giải phương trình ${\displaystyle \frac{3x-1}{2}}\le x+2$.

$\begin{array}{l}{\displaystyle \frac{3x-1}{2}}\le x+2\\ \iff 3x-1\le 2\left(x+2\right)\\ \iff 3x-1\le 2x+4\\ \iff 3x-2x\le 4+1\\ \iff x\le 5\end{array}$

Vậy $x\le 5$ thì giá trị của biểu thức ${\displaystyle \frac{3x-1}{2}}$ không lớn hơn giá trị của biểu thức $x+2$.

Câu 5:

Phương pháp:

Các bước giải phương trình chứa dấu giá trị tuyệt đối.

- Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đôi

- Bước 2: Giải các phương trình không có dấu giá trị tuyệt đối

- Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét

- Bước 4: Kết luận nghiệm.

Lời giải:

$|x+4|=x+4$ nếu $x+4\ge 0\iff x\ge -4$.

$|x+4|=-\left(x+4\right)$ nếu $x+4<0\iff x<-4$.

- Với $x\ge -4$ ta có:

$\begin{array}{l}x+4=3x-5\\ \iff x-3x=-5-4\\ \iff -2x=-9\\ \iff x={\displaystyle \frac{9}{2}}\text{ (t/m)}\end{array}$

- Với $x<-4$ ta có:

$\begin{array}{l}-\left(x+4\right)=3x-5\\ \iff -x-4=3x-5\\ \iff -x-3x=-5+4\\ \iff -4x=-1\\ \iff x={\displaystyle \frac{1}{4}}\text{ (loại)}\end{array}$

Vậy phương trình đã cho có nghiệm $x={\displaystyle \frac{9}{2}}$

Câu 1. (1,5 điểm). Hãy chọn khẳng định đúng. Cho $c<d$, ta có:

(A) $c-2>d-2$

(B) $-3c<-3d$

(C) $3c+2>3d+2$

(D) $3c-2<3d-2$

Câu 2. (1,5 điểm). Hãy chọn khẳng định đúng. Bất phương trình $7x+14<0$ có tập nghiệm biểu diễn bởi hình vẽ sau:

Câu 3. (2,0 điểm). Giải bất phương trình $-2x+5>0$ và biểu diễn tập nghiệm trên trục số.

Câu 4. (3,0 điểm). Tìm $x$ sao cho:

a) Giá trị của biểu thức $2(x+3)$ nhỏ hơn giá trị của biểu thức $5-x$.

b) Giá trị của biểu thức $x-2$ không nhỏ hơn giá trị của biểu thức ${\displaystyle \frac{10-x}{3}}$.

Câu 5. (2,0 điểm). Giải phương trình $|-4x|=2x+12$.

Câu 1:

Phương pháp:

Sử dụng:

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

- Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Lời giải:

$\begin{array}{l}c<d\\ \iff 3c<3d\\ \iff 3c-2<3d-2\end{array}$

Chọn D.

Câu 2:

Phương pháp:

 - Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác $0$ để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

$\begin{array}{l}7x+14<0\\ \iff 7x<-14\\ \iff x<\left(-14\right):7\\ \iff x<-2\end{array}$

Vậy phương trình có nghiệm là $x<-2$.

Biểu diễn tập nghiệm của bất phương trình trên trục số như sau:

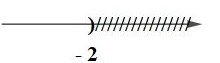
Chọn C.

Phương pháp:

- Áp dụng quy tắc chuyển vế và quy tắc nhân với một số khác $0$ để tìm nghiệm của bất phương trình. Từ đó ta biểu diễn tập nghiệm tìm được trên trục số.

Lời giải:

$\begin{array}{l}-2x+5\ge 0\\ \iff -2x\ge -5\\ \iff x\le {\displaystyle \frac{5}{2}}\end{array}$

Vậy nghiệm của bất phương trình là $x\le {\displaystyle \frac{5}{2}}$.

Biểu diễn tập nghiệm trên trục số như sau

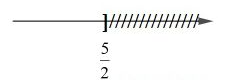
Câu 4:

Phương pháp:

a) Giá trị của biểu thức $2(x+3)$ nhỏ hơn giá trị của biểu thức $5-x$ tức là ta giải phương trình $2\left(x+3\right)<5-x$.

b) Giá trị của biểu thức $x-2$ không nhỏ hơn giá trị của biểu thức ${\displaystyle \frac{10-x}{3}}$ tức là ta giải phương trình $x-2\ge {\displaystyle \frac{10-x}{3}}$

Lời giải:

a) Giá trị của biểu thức $2(x+3)$ nhỏ hơn giá trị của biểu thức $5-x$ tức là ta giải phương trình $2\left(x+3\right)<5-x$.$\begin{array}{l}2\left(x+3\right)<5-x\\ \iff 2x+6<5-x\\ \iff 2x+x<5-6\\ \iff 3x<-1\\ \iff x<{\displaystyle \frac{-1}{3}}\end{array}$

Vậy $x<{\displaystyle \frac{-1}{3}}$ thì giá trị của biểu thức $2(x+3)$ nhỏ hơn giá trị của biểu thức $5-x$.

b) Giá trị của biểu thức $x-2$ không nhỏ hơn giá trị của biểu thức ${\displaystyle \frac{10-x}{3}}$ tức là ta giải phương trình $x-2\ge {\displaystyle \frac{10-x}{3}}$.

$\begin{array}{l}x-2\ge {\displaystyle \frac{10-x}{3}}\\ \iff 3\left(x-2\right)\ge 10-x\\ \iff 3x-6\ge 10-x\\ \iff 3x+x\ge 10+6\\ \iff 4x\ge 16\\ \iff x\ge 4\end{array}$

Phương pháp:

Các bước giải phương trình chứa dấu giá trị tuyệt đối.

- Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đôi

- Bước 2: Giải các phương trình không có dấu giá trị tuyệt đối

- Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét

- Bước 4: Kết luận nghiệm.

Lời giải:

$|-4x|=-4x$ nếu $-4x\ge 0$ hay $x\le 0$.

$|-4x|=4x$ nếu $-4x<0$ hay $x>0$.

- Nếu $x\le 0$ ta có:

$\begin{array}{l}-4x=2x+12\\ \iff -4x-2x=12\\ \iff -6x=12\\ \iff x=-2\text{ (t/m)}\end{array}$

- Nếu $x>0$ ta có:

$\begin{array}{l}4x=2x+12\\ \iff 4x-2x=12\\ \iff 2x=12\\ \iff x=6\text{ (t/m)}\end{array}$