Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 3 sách Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:

Giải SGK Toán 7 (Cánh diều): Bài tập cuối chương 3

Bài tập 1 trang 87 Toán lớp 7: Quan sát Hình 11, Hình 12 và chọn chữ Đ (đúng), S (sai) thích hợp cho ô trống trong bảng sau:

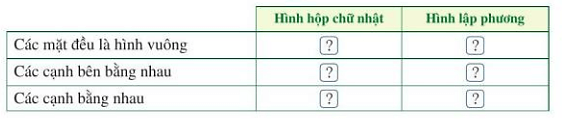
Lời giải:

Bài tập 2 trang 87 Toán lớp 7:

a) Cho một hình lăng trụ đứng có độ dài cạnh bên là 10 cm và đáy là tam giác. Biết tam giác đó có độ dài các cạnh lần lượt là 4 cm, 5 cm, 6 cm. Tính diện tích xung quanh của hình lăng trụ đứng đã cho.

b) Cho một hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang cân đó có độ dài cạnh bên là 13 cm, độ dài hai đáy là 8 cm, 18 cm và chiều cao là 12 cm. Tính diện tích toàn phần (tức là tổng diện tích các mặt) của hình lăng trụ đứng đã cho.

Lời giải:

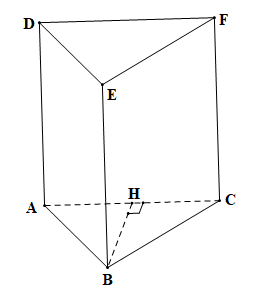
a) Chu vi đáy của hình lăng trụ đứng tam giác là: 4 + 5 + 6 =15 (cm)

Diện tích xung quanh hình lăng trụ đứng tam giác là: Sxq = 15.10 = 150 ($c{m}^2$)

b) Chu vi đáy của hình lăng trụ đứng tứ giác là: 13 + 13 + 8 + 18 = 52 (cm)

Diện tích xung quanh của hình lăng trụ đứng đó là: Sxq = 52.20 = 1040 ($c{m}^2$)

Diện tích một đáy hình lăng trụ đứng đó là: 

S = $\frac{1}{2}\left(8+18\right).12=\frac{1}{2}\mathrm{.26.12}=156$ ($c{m}^2$).

Diện tích toàn phần hình lăng trụ đứng đó là: 

Stp = 156.2 + 1040 = 1352 ($c{m}^2$).

Bài tập 3 trang 87 Toán lớp 7:

a) Một hình lập phương có độ dài cạnh là 3 cm. Tính thể tích của hình lập phương đó.

b) Một hình lập phương mới có độ dài cạnh gấp đôi độ dài cạnh của hình lập phương ban đầu. Tính thể tích của hình lập phương mới và cho biết thể tích của hình lập phương mới gấp bao nhiêu lần thể tích của hình lập phương ban đầu.

Lời giải:

a) Thể tích hình lập phương với độ dài cạnh là 3 cm là: V = 33 = 27 ($c{m}^3$)

b) Vì độ dài hình lập phương mới gấp 2 lần độ dài hình lập phương ban đầu nên độ dài cạnh hình lập phương mới là 2.3 = 6 (cm).

Thể tích hình lập phương mới là: 

V’ = 63 = 216 ($c{m}^3$)

Tỉ số thể tích của hình lập phương mới so với hình lập phương ban đầu là: 

$\frac{V^{\text{'}}}{V}=\frac{216}{27}=\frac{8}{1}$

Vậy thể tích hình lập phương mới gấp 8 lần thể tích hình lập phương ban đầu.

Bài tập 4 trang 87 Toán lớp 7: Hình 34 mô tả một xe chở hai bánh mà thùng chứa của nó có dạng lăng trụ đứng tam giác với các kích thước cho trên hình. Hỏi thùng chứa của xe chở hai bánh có thể tích bằng bao nhiêu?

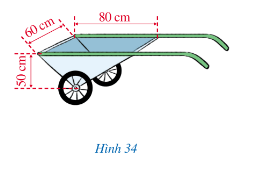
Lời giải:

Ta biểu diễn thùng chứa của xe thành hình lăng trụ đứng tam giác như hình vẽ trên với hai đáy là ABC và DEF, chiều cao của đáy là BH = 50 cm, độ dài cạnh bên là BE = 60 cm, cạnh đáy AC = 80 cm.

Ta có: 

Diện tích đáy ABC của thùng chứa là: 

S =  $\frac{1}{2}.AH.BC=\frac{1}{2}.50.80=2000$ ($c{m}^2$)

Thể tích thùng chứa của xe là: 

V = S.h = 2 000.60 = 120 000 ($c{m}^3$).

Vậy thể tích thùng chứa của xe là 120 000 $c{m}^3$.

Bài tập 5 trang 87 Toán lớp 7: Một ngôi nhà có cấu trúc và kích thước được mô tả như Hình 35.

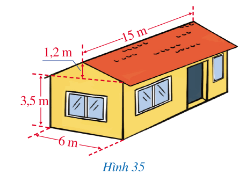
Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó.

Hướng dẫn: Phần không gian của ngôi nhà đó có thể chia thành 2 phần: phần không gian có dạng một hình hộp chữ nhật và phần không gian còn lại có dạng một hình lăng trụ đứng tam giác.

Lời giải:

Thể tích phần không gian của ngôi nhà có dạng hình hộp chữ nhật là: 

V1 = 3,5.6.15 = 315 ($m^3$)

Diện tích đáy phần không gian mái nhà có hình lăng trụ đứng là: 

S = $\frac{1}{2}.1,2.6=3,6 \left(m^2\right)$

Thể tích phần không gian có hình lăng trụ đứng là: 

V2 = 3,6 . 15 = 54 ($m^3$)

Thể tích phần không gian được giới hạn bởi ngôi nhà đó là: 

54 + 315 = 369 ($m^3$).

Vậy thể tích phần không gian được giới hạn bởi ngôi nhà đó là 369 $m^3$.