Với Giải SBT Toán 10 Tập 1 trong Bài 2: Hệ bất phương trình bậc nhất hai ẩn Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

Một bãi đậu xe ban đêm có diện tích đậu xe là 150 m^2 (không tính lối đi cho xe ra vào)

Bài 3 trang 33 SBT Toán 10 Tập 1: Một bãi đậu xe ban đêm có diện tích đậu xe là 150 m² (không tính lối đi cho xe ra vào). Cho biết xe du lịch cần diện tích 3 m2/chiếc và phải trả phí 40 nghìn đồng, xe tải cần diện tích 5 m2/chiếc và phải trả phí 50 nghìn đồng. Nhân viên quản lí không thể phục vụ quá 40 xe một đêm. Hãy tính số lượng xe mỗi loại mà chủ bãi xe có thể cho đăng kí đậu xe để có doanh thu cao nhất.

Lời giải:

Gọi x là số xe du lịch và y là số xe tải mà chủ bãi xe nên cho đậu một đêm. (x ≥ 0, y ≥ 0).

Vì nhân viên quản lí không thể phục vụ quá 40 xe một đêm nên x + y ≤ 40.

Diện tích cần dùng để đỗ x xe du lịch là: 3x (m²).

Diện tích cần dùng để đỗ y xe tải là: 5y (m²).

Do bãi đậu xe có diện tích đậu xe là 150 m² (không tính lối đi cho xe ra vào), do đó ta có 3x + 5y ≤ 150.

Từ đó ta có hệ bất phương trình $\left\{\begin{array}{l}x+y\le 40\\ 3x+5y\le 150\\ x\ge 0\\ y\ge 0\end{array}\right.$.

Để biểu diễn miền nghiệm của hệ bất phương trình trên, ta biểu diễn miền nghiệm của mỗi bất phương trình của hệ trên mặt phẳng Oxy và xét phần giao.

+ Vẽ đường thẳng x + y = 40 đi qua hai điểm (0; 40) và (40; 0).

Xét gốc tọa độ O không thuộc đường thẳng x + y = 40, ta có: 0 + 0 = 0 < 40.

Do đó, miền nghiệm của bất phương trình x + y ≤ 40 là nửa mặt phẳng có bờ là đường thẳng x + y = 40, chứa điểm O, kể cả đường thẳng x + y = 40.

+ Vẽ đường thẳng 3x + 5y = 150 đi qua hai điểm (0; 30) và (50; 0).

Xét gốc tọa độ O không thuộc đường thẳng 3x + 5y = 150, ta có: 3 . 0 + 4 . 0 = 0 < 150.

Do đó, miền nghiệm của bất phương trình 3x + 5y ≤ 150 là nửa mặt phẳng có bờ là đường thẳng 3x + 5y = 150, chứa điểm O, kể cả đường thẳng 3x + 5y = 150.

+ Miền nghiệm của bất phương trình x ≥ 0 chính là nửa mặt phẳng có bờ là đường thẳng Oy, nằm bên phải trục Oy, bao gồm cả đường thẳng Oy.

+ Miền nghiệm của bất phương trình y ≥ 0 chính là nửa mặt phẳng có bờ là đường thẳng Ox, nằm bên trên trục Ox, bao gồm cả đường thẳng Ox.

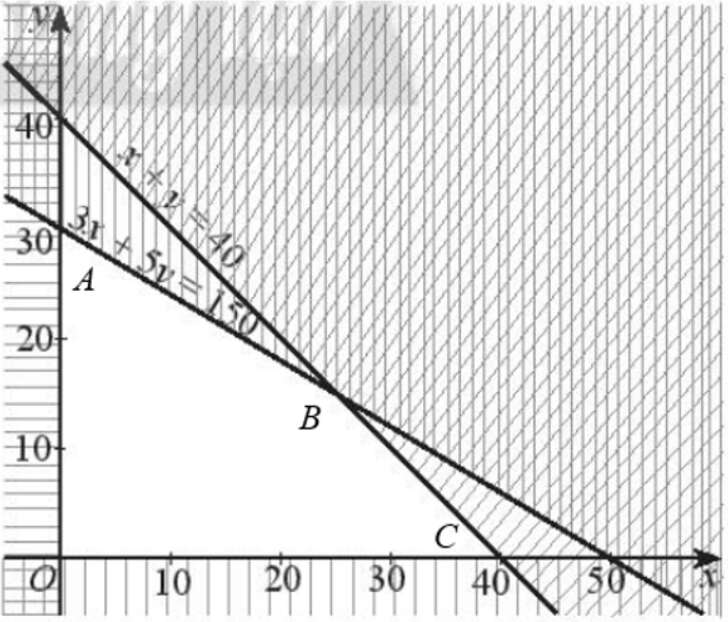
Miền không bị gạch chéo bao gồm cả các cạnh trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiện của hệ bất phương trình trên. Do đó miền nghiệm của hệ bất phương trình trên chính là miền tứ giác OABC (kể cả bờ) với O(0; 0), A(0; 30), B(25; 15), C(40; 0).

Số tiền chủ bãi xe thu được khi cho đậu x xe du lịch và y xe tải là F = 40x + 50y (nghìn đồng).

Người ta chứng minh được rằng F đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác OABC.

Ta có: F(0; 0) = 40 . 0 + 50 . 0 = 0

F(0; 30) = 40 . 0 + 50 . 3 = 150

F(25; 15) = 40 . 25 + 50 . 15 = 1 750

F(40; 0) = 40 . 40 + 50 . 0 = 1 600

Do đó, F_max = 1 750 (nghìn đồng) tại (x; y) = (25; 15).

Vậy để có doanh thu cao nhất, chủ bãi xe có thể cho đăng kí 25 chiếc xe du lịch và 15 chiếc xe tải.

Xem thêm các bài giải sách bài tập Toán lớp 10 sách Chân trời sáng tạo hay, chi tiết khác:

• Bài 1 trang 33 SBT Toán 10 Tập 1: Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau đây:
• Bài 2 trang 33 SBT Toán 10 Tập 1: Bạn Bích có 500 g bột gạo để pha hai loại nước hồ tráng bánh đa và bánh xèo.
• Bài 4 trang 34 SBT Toán 10 Tập 1: Cho biết mỗi kilôgam thịt bò giá 250 nghìn đồng, trong đó có chứa khoảng 800 đơn vị protein