Với Giải SBT Toán 7 trang 92 Tập 1 trong Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giácbài tập Toán lớp 7 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 92.
Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có đáy là hình thang ABCD vuông tại B
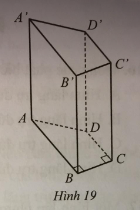
Bài 11 trang 92 sách bài tập Toán 7: Cho hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ có đáy là hình thang ABCD vuông tại B (AB song song với CD) với , , , và chiều cao (Hình 19).
a) Tính diện tích xung quanh của hình lăng trụ ABCD.A’B’C’D’.
b) Tính thể tích của hình lăng trụ ABCD.A’B’C’D’.
c) Người ta dán giấy màu (bên ngoài) tất cả các mặt của hình lăng trụ. Tính số tiền người đó phải trả, biết rằng giá tiền dán giấy màu mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 150 000 đồng.
Lời giải:
a) Đổi 100 cm = 10 dm.
Diện tích xung quang của hình lăng trụ ABCD.A’B’C’D’ là:
.
b) Diện tích đáy ABCD của hình lăng trụ là:
.
Thể tích của hình lăng trụ ABCD.A’B’C’D’ là:
.
c) Tổng diện tích tất cả các mặt của hình lăng trụ là:
.
Số tiền người đó phải trả là:
(đồng).
Xem thêm lời giải vở bài tập Toán lớp 7 Cánh diều với cuộc sống hay, chi tiết khác:
Bài 10 trang 92 sách bài tập Toán 7: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?...
Bài 14 trang 93 sách bài tập Toán 7: Sắp xếp các hình sau theo thứ tự thể tích giảm dần:...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.