Cho tam giác ABC cân tại A (góc A<90 độ). Hai đường cao BE và CF cắt nhau tại H

Với giải Bài 1 trang 84 Toán lớp 7 Chân trời sáng tạo chi tiết trong Bài tập cuối Chương 8 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán 7 Bài tập cuối Chương 8

Bài 1 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A ( $\hat{A} < 90^{o}$ ). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rẳng $Δ B F C = Δ C E B$

b) Chứng minh rằng $Δ A E H = Δ A F H$

c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.

Phương pháp giải

a) Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông

b) Từ câu a ta chứng minh 2 tam giác AHF = tam giác AHE nhờ những cạnh của 2 tam giác chứng minh được bằng nhau từ câu trên

c) Ta chứng minh AI và AH cùng là phân giác của góc A

Lời giải

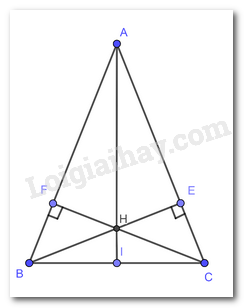
a) Xét ΔBFC và ΔCEB có:

BC là cạnh chung

$\overset{⏜}{B} = \overset{⏜}{C}$ (ΔABCcân tại A)

$\overset{⏜}{B E C} = \overset{⏜}{C F B} = 90 °$

⇒ΔBFC=ΔCEB (cạnh huyền – góc nhọn )

b) Vì $Δ B F C = Δ C E B \Rightarrow$ BF = EC (2 cạnh tương ứng)

Mà AB = AC ( $Δ A B C$ cân tại A)

$\Rightarrow$ AF = AE (AB – BF = AC – EC )

Xét $Δ A E H$ và $Δ A F H$ ta có :

AF = AE (chứng minh trên)

AH cạnh chung

$\hat{H F A} = \hat{H E A} = 90^{o}$

$\Rightarrow Δ A E H = Δ A F H$ (cạnh huyền - cạnh góc vuông)

c) Vì CF, BE là những đường cao của tam giác ABC và H là giao điểm của chúng

$\Rightarrow$ H là trực tâm của tam giác ABC

$\Rightarrow$ AH vuông góc với BC (1)

Xét $Δ A I C$ và $Δ A I B$ có :

IB = IC (I là trung điểm BC)

AI là cạnh chung

AB = AC ( tam giác ABC cân tại A)

$\Rightarrow Δ A I C = Δ A I B (c - c - c)$

$\Rightarrow \hat{A I C} = \hat{A I B}$ (2 góc tương ứng) Mà chúng ở vị trí kề bù $\Rightarrow \hat{A I C} = \hat{A I B} = 90^{o}$ $\Rightarrow A I ⊥ B C$ (2)