Toán 7 Chân trời sáng tạo: Bài tập cuối Chương 8

Lê Hoàng Thảo Vy Ngày: 13-01-2023 Lớp 7

673

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối Chương 8sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:

Giải Toán lớp 7 trang 84 Bài tập cuối Chương 8

Bài 1 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A ( $\hat{A} < 90^{o}$ ). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rẳng $Δ B F C = Δ C E B$

b) Chứng minh rằng $Δ A E H = Δ A F H$

c) Gọi I là trung điểm BC. Chứng minh rằng ba điểm A,H,I thẳng hàng.

Phương pháp giải

a) Ta sử dụng định lí cạnh huyền – góc nhọn trong tam giác vuông

b) Từ câu a ta chứng minh 2 tam giác AHF = tam giác AHE nhờ những cạnh của 2 tam giác chứng minh được bằng nhau từ câu trên

c) Ta chứng minh AI và AH cùng là phân giác của góc A

Lời giải

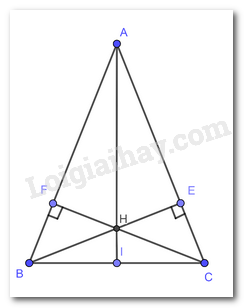
a) Xét ΔBFC và ΔCEB có:

BC là cạnh chung

$\overset{⏜}{B} = \overset{⏜}{C}$ (ΔABCcân tại A)

$\overset{⏜}{B E C} = \overset{⏜}{C F B} = 90 °$

⇒ΔBFC=ΔCEB (cạnh huyền – góc nhọn )

b) Vì $Δ B F C = Δ C E B \Rightarrow$ BF = EC (2 cạnh tương ứng)

Mà AB = AC ( $Δ A B C$ cân tại A)

$\Rightarrow$ AF = AE (AB – BF = AC – EC )

Xét $Δ A E H$ và $Δ A F H$ ta có :

AF = AE (chứng minh trên)

AH cạnh chung

$\hat{H F A} = \hat{H E A} = 90^{o}$

$\Rightarrow Δ A E H = Δ A F H$ (cạnh huyền - cạnh góc vuông)

c) Vì CF, BE là những đường cao của tam giác ABC và H là giao điểm của chúng

$\Rightarrow$ H là trực tâm của tam giác ABC

$\Rightarrow$ AH vuông góc với BC (1)

Xét $Δ A I C$ và $Δ A I B$ có :

IB = IC (I là trung điểm BC)

AI là cạnh chung

AB = AC ( tam giác ABC cân tại A)

$\Rightarrow Δ A I C = Δ A I B (c - c - c)$

$\Rightarrow \hat{A I C} = \hat{A I B}$ (2 góc tương ứng) Mà chúng ở vị trí kề bù $\Rightarrow \hat{A I C} = \hat{A I B} = 90^{o}$ $\Rightarrow A I ⊥ B C$ (2)

Từ (1) và (2) $\Rightarrow$ A, H, I thẳng hàng.

Bài 2 trang 84 Toán lớp 7: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng tam giác ABM cân.

b) Chứng minh rằng $Δ A B C = Δ M B C$

Phương pháp giải

a) Ta chứng minh BM = BA thông qua việc chứng minh 2 tam giác BHA và BHM bằng nhau

b) Ta chứng minh góc ABH = góc MBH sau đó chứng minh 2 tam giác đề bài yêu cầu bằng nhau theo trường hợp c-g-c

Lời giải

a) Xét $Δ B H A$ và $Δ B H M$ có :

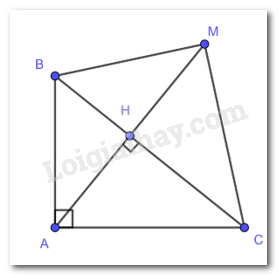
$\hat{B H A} = \hat{B H M} = 90^{o}$

BH cạnh chung

AH = HM (do M đối xứng với A qua H)

$\Rightarrow Δ B H A = Δ B H M (c - g - c)$

$\Rightarrow A B = B M$ (cạnh tương ứng) và $\hat{A B H} = \hat{M B H}$

$\Rightarrow Δ A B M$ cân tại B (2 cạnh bên bằng nhau)

b) Xét $Δ A B C$ và $Δ M B C$ ta có :

AB = BM (câu a)

$\hat{A B H} = \hat{M B H}$ (câu a)

BC cạnh chung

$\Rightarrow Δ A B C = Δ M B C (c - g - c)$

Bài 3 trang 84 Toán lớp 7: Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AD = AC.

b) Chứng minh rằng $\hat{A D H} = \hat{B A H}$

Phương pháp giải

a) Ta chứng minh tam giác ACD cân tại A sau đó suy ra AC = AD

b) Ta chứng minh $\hat{B A H} + \hat{H A C} = 90^{o} = \hat{H A C} + \hat{H C A}$ và $\hat{D} = \hat{C}$

Lời giải

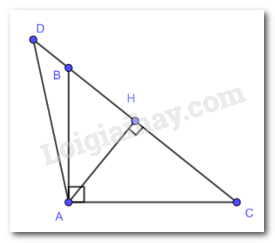
a) Xét $Δ A H D$ và $Δ A H C$ có :

AH chung

DH = HC ( C đối xứng D qua H)

$\hat{A H D} = \hat{A H C} = 90^{o}$

$\Rightarrow Δ A H D = Δ A H C (c - g - c)$

$\Rightarrow A D = A C$ (cạnh tương ứng)

$\Rightarrow Δ A D C$ cân tại A $\Rightarrow \hat{C} = \hat{D}$ (góc tương ứng)(1)

b) Ta có $\hat{B A H} + \hat{H A C} = 90^{o}$ và $\hat{H C A} + \hat{H A C} = 90^{o}$

$\Rightarrow \hat{B A H} = \hat{H C A}$ (2)

Từ (1) và (2) $\Rightarrow \hat{A D H} = \hat{B A H}$

b) Ta có $\hat{B A H} + \hat{H A C} = 90^{o}$ và $\hat{H C A} + \hat{H A C} = 90^{o}$

$\Rightarrow \hat{B A H} = \hat{H C A}$ (2)

Từ (1) và (2) $\Rightarrow \hat{A D H} = \hat{B A H}$

Bài 4 trang 84 Toán lớp 7: Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ $B E ⊥ A N$ (E ∈ AN).

a) Chứng minh rằng BE là tia phân giác của giác ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.

Phương pháp giải

a) Ta chứng minh $\hat{A B E} = \hat{N B E}$ bằng cách chứng minh 2 tam giác BAF và BNF bằng nhau .

b) Ta chứng minh NK song song với CA do có 2 góc so le trong bằng nhau

c) Ta chứng minh góc BGC bằng góc BCG

Lời giải

a) XétΔBAE và ΔBNE có :

BA = BN (giả thiết)

BF cạnh chung

$\overset{⏜}{B E A} = \overset{⏜}{B E N}$

⇒ΔBAE = ΔBNE
(cạnh huyền-cạnh góc vuông)

⇒ $\overset{⏜}{A B F} = \overset{⏜}{N B F}$
(góc tương ứng)

⇒BE là phân giác của góc ABN

b) Vì K là giao của 2 đường cao $\Rightarrow$ K là trực tâm tam giác ABN

$\Rightarrow$ KN vuông góc với AB(1)

Vì CA vuông góc với AB ( tam giác ABC vuông tại A)(2)

Từ (1) và (2) $\Rightarrow$ KN song song với CA (quan hệ cùng vuông góc với 1 đường)

c) Ta có $Δ B A F = Δ B N F (c - g - c)$ do có :

$\hat{B E A} = \hat{B E N}$

BF cạnh chung

BN = BA

$\Rightarrow \hat{B N F} = \hat{B A F}$ (2 góc tương ứng).

Mà $\hat{B A F} = 90^{\circ}$

$\Rightarrow \hat{B N F} = \hat{B A F} = 90^{o}$

$\Rightarrow G N ⊥ B C$

Ta có CA và GN là 2 đường cao của tam giác GBC

$\Rightarrow$ F là trực tâm của tam giác GBC

$\Rightarrow$ BF vuông góc với GC tại P

Xét $Δ B G P$ và $Δ B C P$ ta có :

BP cạnh chung

$\hat{B P C} = \hat{B P G} = 90^{o}$

$\hat{P B C} = \hat{P B G}$

$\Rightarrow Δ B G P = Δ B C P (c - g - c)$

$\Rightarrow B C = B G$ (2 cạnh tương ứng)

$\Rightarrow$ Tam giác GBC cân tại B

Bài 5 trang 84 Toán lớp 7: Cho tam giác nhọn ABC (AB < AC), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng $\hat{B M N} = \hat{H A C}$

b) Kẻ $M I ⊥ A H$ (I ∈ AH), gọi K là giao điểm của AH và BM. Chứng minh rằng I là trung điểm của AK.

Phương pháp giải

a) Ta xét tam giác BMC cân tại M nên $\hat{M B C} = \hat{M C B}$

Nên $\hat{B M N} = \hat{H A C} = 90^{o} - \hat{M B C} = 90^{o} - \hat{M B C}$

b) Ta chứng minh I là trung điểm của AK do $Δ M A I = Δ M K I$ (g-c-g)

Lời giải

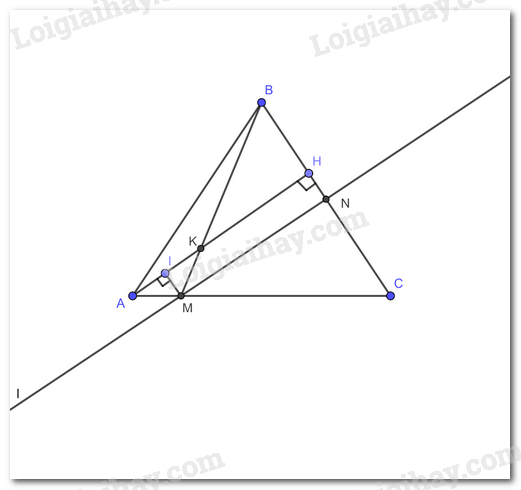
a) Xét tam giác BMC cân tại M (Do M thuộc đường trung trực của BC nên MB = MC) có : $\hat{M B C} = \hat{M C B}$ (góc tương ứng)

Mà $\hat{B M N} = 90^{o} - \hat{M B C}$ và $\hat{H A C} = 90^{o} - \hat{B C M}$

$\Rightarrow$ $\hat{B M N} = \hat{H A C}$

b) Ta có MN⫽AH (do cùng vuông góc với BC)

$\Rightarrow \hat{A K M} = \hat{K M N}$ (2 góc so le trong)

Mà $\hat{B M N} = \hat{H A C}$ ( chứng minh a)

$\Rightarrow \hat{K A M} = \hat{A K M}$ ( do cùng = $\hat{B M N}$ )

Xét $Δ M I A$ và $Δ M I K$ có :

IM cạnh chung

$\hat{K A M} = \hat{A K M}$

$\hat{A I M} = \hat{M I K} = 90^{o}$

$\Rightarrow Δ M I A = Δ M I K$ (cạnh góc vuông-góc nhọn)

$\Rightarrow$ AI = IK (cạnh tương ứng)

$\Rightarrow$ I là trung điểm AK

Bài 6 trang 84 Toán lớp 7: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng $Δ$ MFN = $Δ$ PFD

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.

Phương pháp giải

a) Chứng minh $Δ$ MFN = $Δ$ PFD theo trường họp cạnh góc cạnh

Sử dụng tính chất của điểm đối xứng qua một điểm, trung điểm của 1 đoạn thẳng và 2 góc đối đỉnh

b) Chứng minh H là trọng tâm của tam giác MPD sau đó dựa vào tính chất ta suy ra M, H, K thẳng hàng

Lời giải

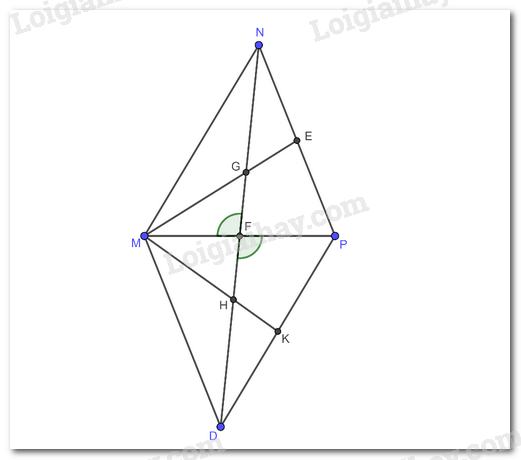
a) Vì N đối xứng với D qua F (theo giả thiết)

Nên NF = DF (1)

Vì F là trung điểm của MP (theo giả thiết)

Nên MF = PF (2)

Vì góc NFM và góc PFD ở vị trí đối đỉnh nên 2 góc bằng nhau (3)

Từ (1), (2) và (3) $\Rightarrow$ $Δ$ MFN = $Δ$ PFD (c-g-c)

b) Xét tam giác MPD có :

F là trung điểm MD,

K là trung điểm DP (theo giả thiết)

Mà 2 đường trung tuyến của tam giác MPD là DF và MK cắt nhau tại H

$\Rightarrow$ H là trọng tâm $Δ$ MPD

$\Rightarrow$ M, H, K thẳng hàng

Bài 7 trang 84 Toán lớp 7: Cho tam giác ABC vuông tại A có AB = $\frac{1}{2}$ AC, AD là tia phân giác $\hat{B A C}$ (D ∈ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH $⊥$ KC.

Phương pháp giải

a) Chứng minh BD = DE thông qua việc chứng minh 2 tam giác BAD và EAD bằng nhau

b) Chứng minh $Δ$ CDK cân tại D do có 2 cạnh bên DK = DC

c) Chứng minh $Δ$ KAC vuông cân tại A và AD là phân giác nên cũng là đường cao của $Δ$ KAC $\Rightarrow$ AH $⊥$ KC

Lời giải

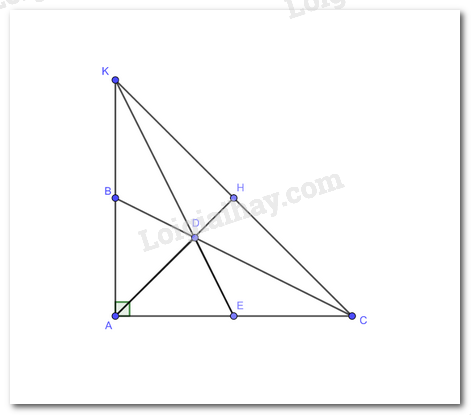
a) Xét ΔBAD và ΔEAD có :

AD là cạnh chung

AB = AE = $\frac{1}{2} A C$

$\overset{⏜}{B A D} = \overset{⏜}{E A D}$ (do AD là phân giác góc A)

⇒ΔBAD = ΔEAD (c-g-c)

⇒DE = DB (cạnh tương ứng) và $\overset{⏜}{A B D} = \overset{⏜}{A E D}$ (góc tương ứng)

b) Xét $Δ$ KAE và $Δ$ CAB có :

AE = AB

$\hat{A B D} = \hat{A E D}$ (chứng minh a)

Góc A chung

$\Rightarrow Δ K A E = Δ C A B$ (g-c-g)

$\Rightarrow$ KE = CB (cạnh tương ứng)

Mà KE = ED + DK và CB = BD + DC

$\Rightarrow$ KE – ED = CB – BD $\Rightarrow$ DK = DC

$\Rightarrow$ $Δ D C K$ cân tại D

+) Xét $Δ$ KDB và $Δ$ CDE có :

DB = DE

DK = DC

$\hat{K D B} = \hat{C D E}$ (2 góc đối đỉnh)

$\Rightarrow Δ K D B = Δ C D E$ (c-g-c)

$\Rightarrow$ KB = EC $\Rightarrow$ KB = AB (do cùng = EC) $\Rightarrow$ B là trung điểm AK

c) Vì $Δ K A E$ = $Δ C A B$ (chứng minh trên)

$\Rightarrow$ AK = AC (cạnh tương ứng)

$\Rightarrow$ $Δ$ AKC vuông cân tại A

Mà AD là phân giác góc A nên AD sẽ vừa là phân giác vừa là đường cao của $Δ$ AKC

$\Rightarrow$ AD $⊥$ KC

$\Rightarrow$ AH $⊥$ KC (do H $i n$ AD)

Bài 8 trang 84 Toán lớp 7: Ở Hình 1, cho biết AE = AF và $\hat{A B C} = \hat{A C B}$ . Chứng minh AH là đường trung trực của BC.

Phương pháp giải

Ta chứng minh A và H cùng thuộc đường trung trực của đoạn BC thông qua chứng minh chúng cách đều 2 đầu mút của đoạn BC.

Lời giải

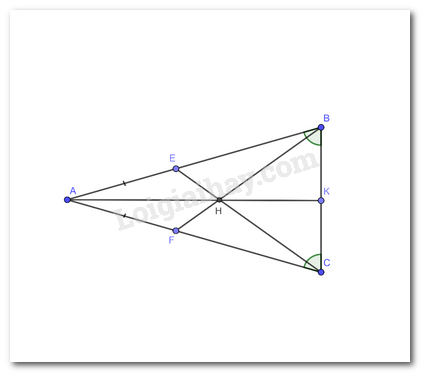
Theo giả thiết ta có tam giác ABC cân tại A do có 2 góc đáy bằng nhau

⇒A cách đều 2 đều B, C

⇒A thuộc trung trực đoạn thẳng BC (1) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Xét ΔAEC và ΔAFB ta có :

AE = AF

Góc A chung

AC = AB

⇒ ΔAEC=ΔAFB (c-g-c)

⇒ $\overset{⏜}{E C A} = \overset{⏜}{F B A}$ (góc tương ứng)

Ta có: $\hat{A B C} = \hat{A B F} + \hat{F B C}$

$\hat{A C B} = \hat{A C E} + \hat{E C B}$

Mà $\hat{A C B} = \hat{A B C}$ (giả thiết) và $\hat{E C A} = \hat{F B A}$ (chứng minh trên)

$\Rightarrow \hat{E C B} = \hat{F B C}$ $\Rightarrow$ $Δ$ HBC cân tại H do có 2 góc đáy bằng nhau

$\Rightarrow$ H cách đều BC $\Rightarrow$ H thuộc trung trực BC (2) (Tính chất điểm cách đều 2 đầu mút đoạn thẳng)

Từ (1) và (2) $\Rightarrow$ AH là trung trực của BC

Bài 9 trang 84 Toán lớp 7: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng $\hat{E B H} = \hat{A C M}$

c) Chứng minh rằng $E B ⊥ B C$

Phương pháp giải

a)Ta chứng minh $Δ$ BME có 2 cạnh bên hoặc 2 góc đáy bằng nhau thông qua việc chứng minh 2 tam giác EHB và MHB bằng nhau.

b)Ta chứng minh $\hat{E B H} = \hat{A C M}$ do cùng = $\hat{M B H}$

c)Ta chứng minh $\hat{E B H} + \hat{B C E} = 90^{o}$

Lời giải

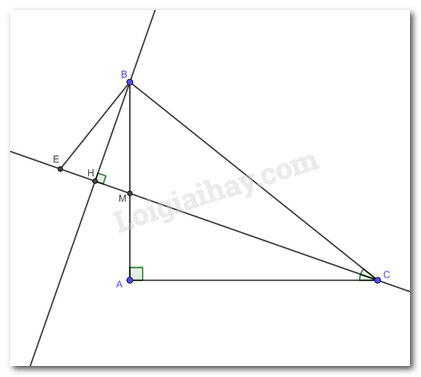
a)Xét $Δ$ BHE và $Δ$ BHM có :

BH là cạnh chung

EH = HM (do M đối xứng E qua H)

$\hat{B H E} = \hat{B H M} = 90^{o}$

$\Rightarrow$ $Δ$ BHE = $Δ$ BHM (c-g-c)

$\Rightarrow$ BM = BE (cạnh tương ứng)

và $\hat{E B H} = \hat{M B H}$ (góc tương ứng) (1)

$\Rightarrow$ $Δ$ BEM cân tại B (2 cạnh bên bằng nhau)

b)Xét $Δ$ BHM vuông tại H $\Rightarrow \hat{B M H} + \hat{M B H} = 90^{o}$

Xét $Δ$ AMC vuông tại A $\Rightarrow \hat{A M C} + \hat{M C A} = 90^{o}$

Mà $\hat{H M B} = \hat{A M C}$ (2 góc đối đỉnh)

$\Rightarrow \hat{M C A} = \hat{M B H} = 90^{o} - \hat{A M C} = 90^{o} - \hat{H M B}$ (2)

Từ (1) và (2) $\Rightarrow \hat{E B H} = \hat{A C M}$

c)Vì $\hat{B C M} = \hat{A C M}$ (do CM là phân giác góc C)

$\Rightarrow \hat{E B H} = \hat{B C M}$ (cùng bằng $\hat{A M C}$ ) (3)

Xét $Δ$ EHB vuông tại H có $\hat{E B H} + \hat{B E H} = 90^{o}$ (4)

Từ (3) và (4) $\Rightarrow \hat{B M C} + \hat{B E H} = 90^{o}$

$\Rightarrow \hat{E B C} = 90^{o} \Rightarrow E B ⊥ B C$

Bài 10 trang 84 Toán lớp 7: Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Phương pháp giải

Ta chứng minh N là trực tâm của tam giác MIK

Lời giải

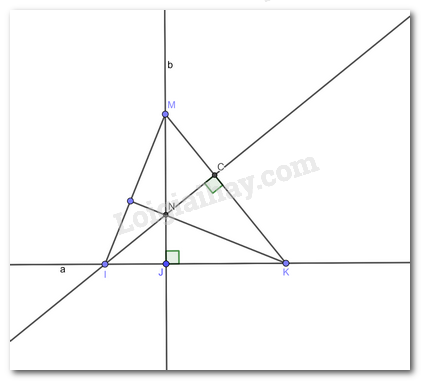
Vì b vuông góc với a tại J (theo giả thiết) và M thuộc b

$\Rightarrow M J ⊥ I K$ (1)

Vì đường thẳng qua I vuông góc với MK và cắt b tại N (gọi C là giao của MK và đường thẳng qua I vuông góc với MK)

$\Rightarrow M K ⊥ I C$ (2)

Từ (1) và (2) $\Rightarrow$ N là trực tâm ΔMIK

$\Rightarrow$ NK là đường cao của ΔMIK (Các đường cao trong tam giác đi qua trực tâm)

$\Rightarrow$ KN $⊥$ MI

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương