Toptailieu.vn giới thiệu giải bài tập Chuyên đề Toán 10 Bài 7: Parabol sách Chân trời sáng tạo hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề học tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Giải bài tập Chuyên đề Toán 10 Bài 7: Parabol
1. Tính đối xứng của đường parabol
Lời giải:
M(x0; y0) thuộc (P) thì y20=2px0.
Có (-y0)2=y20=2px0 nên M'(x0; –y0) cũng thuộc (P).
a) (P1): y2 = 2x;
b) (P2): y2 = x;
c) (P3):y2=15x.
Lời giải:
a) Có 2p = 2, suy ra p = 1.
Toạ độ tiêu điểm của parabol là F(12;0).
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -12
Trục đối xứng của parabol là trục Ox.
b) Có 2p = 1, suy ra p = 12
Toạ độ tiêu điểm của parabol là F(14;0).
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -14
Trục đối xứng của parabol là trục Ox.
c) Có 2p = 15 suy ra p = 110
Toạ độ tiêu điểm của parabol là F(120;0).
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -120
Trục đối xứng của parabol là trục Ox.
Lời giải:
Có JA = √(2-x)2+(0-y)2=√(2-x)2+y2.
Khoảng cách từ J đến d là: d(J; d) = |x + 2|.
Đường tròn (C) luôn đi qua A và tiếp xúc với d ⇔ JA = d(J; d)
⇔√(2-x)2+y2=|x+2|
⇔(2-x)2+y2=|x+2|2
⇔(4-4x+x2)+y2=x2+4x+4
⇔y2=8x.
Vậy (L) là một parabol có phương trình y2 = 8x.
2. Bán kính qua tiêu và tâm sai của parabol
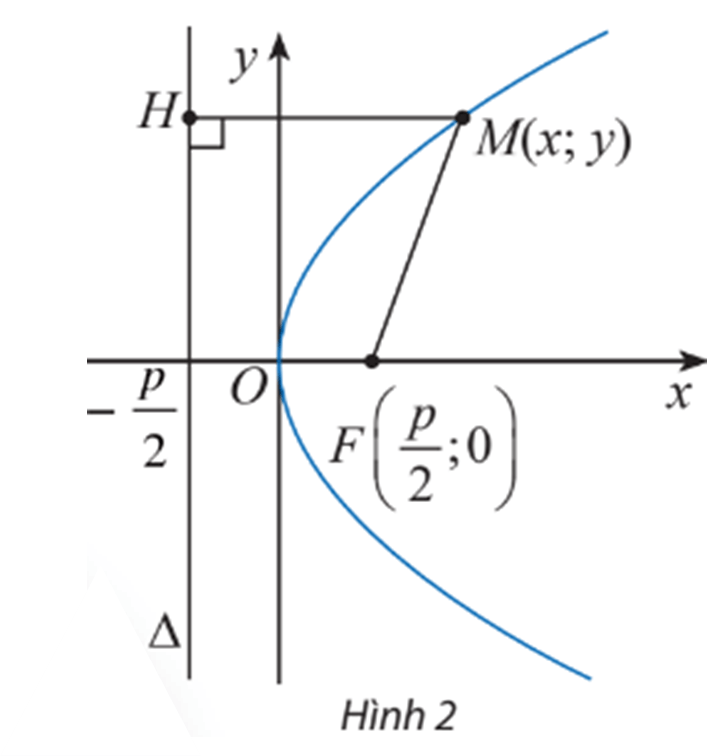
Lời giải:
Vì M thuộc (P) nên y2 = 2px.
Khoảng cách từ điểm M đến tiêu điểm F là: MF = √(x-p2)2+(y-0)2
=√x2-px+p24+y2=√x2-px+p24+2px=√x2+px+p24
=√(x+p2)2=|x+p2|=x+p2 (vì x + p2 > 0).
Thực hành 2 trang 58 Chuyên đề Toán 10:
a) Điểm M1(1; –4) trên (P1): y2 = 16x;
b) Điểm M2(3; –3) trên (P2): y2 = 3x;
c) Điểm M3(4; 1) trên (P3): y2=14x.
Lời giải:
a) Có 2p = 16, suy ra p = 8.
Bán kính qua tiêu của M1 là: FM1 = x + p2 = 1 + 82 = 5.
b) Có 2p = 3, suy ra p = 32
Bán kính qua tiêu của M2 là: FM2 = x + p2 = 3 +34
c) Có 2p = 14 suy ra p = 18
Bán kính qua tiêu của M3 là: FM3 = x + p2 = 4 + 116 = 6516
Lời giải:
Chọn hệ trục toạ độ sao cho gốc O trùng với đỉnh của parabol và trục Ox trùng với tâm đối xứng của parabol, đơn vị trên hai trục toạ độ là mét.
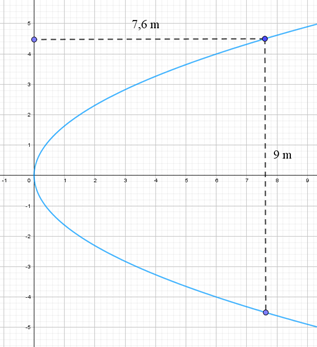
Giả sử parabol có phương trình chính tắc y2 = 2px (p > 0).
Vì chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9 m nên ta có: khi x = 7,6 thì y = 92 = 4,5 ⇒ 4,52 = 2p . 7,6 ⇒ p = 405304
⇒ Toạ độ của tâm ngôi sao là F(p2;0) hay F(405608;0)
⇒ Khoảng cách từ tâm ngôi sao đến đỉnh cổng là 405608mét.

Lời giải:
Có 2p = 0,25 ⇒ p = 0,125 ⇒p2=0,0625.
Khoảng cách từ điểm M(0,25; 0,25) trên ăng-ten đến F bằng khoảng cách từ M đến đường chuẩn x+p2=0 hay x + 0,0625 = 0 của parabol:
MF=x+p2=0,25+0,0625=0,3125.
a) (P1): y2 = 7x;
b) (P2):y2=13x;
c) (P3):y2=√2x.
Lời giải:
a) Có 2p = 7 ⇒ p = 72 ⇒ p2=74
⇒ Toạ độ tiêu điểm của parabol là F(74;0), phương trình đường chuẩn của parabol là x+112=0.
b) Có 2p = 13 ⇒p = 16 ⇒ p2=112
⇒ Toạ độ tiêu điểm của parabol là F(112;0), phương trình đường chuẩn của parabol là x+112=0.
c) Có 2p = √2 ⇒ p = √22 ⇒ p2=√24
⇒Toạ độ tiêu điểm của parabol là F(√24;0), phương trình đường chuẩn của parabol là x+√24=0.
Bài 2 trang 59 Chuyên đề Toán 10: Tính bán kính qua tiêu của điểm đã cho trên các parabol sau:
a) Điểm M1(3; –6) trên (P1): y2 = 12x;
b) Điểm M2(6; 1) trên (P2):y2=16x;
c) Điểm M3(√3;√3) trên (P3):y2=√3x
Lời giải:
a) Có 2p = 12, suy ra p = 6.
Bán kính qua tiêu của M1 là: FM1 = x + p2 = 3 + 62= 6.
b) Có 2p = 16 suy ra p = 112
Bán kính qua tiêu của M2 là: FM2 = x + p2 = 6 + 124 = 14524
c) Có 2p = √3 suy ra p = √32
Bán kính qua tiêu của M3 là: FM3 = x + p2 = √3 + √34 = 5√34
Lời giải:
Có MA = √(14-x)2+(0-y)2=√(14-x)2+y2.
Khoảng cách từ M đến d là: d(M; d) = |x+14|.
Đường tròn (C) luôn đi qua A và tiếp xúc với d ⇔ MA = d(M; d)
⇔√(14-x)2+y2=|x+14|
⇔(14-x)2+y2=|x+14|2
⇔(116-x2+x2)+y2=x2+x2+116
⇔y2=x.
Vậy (P) là một parabol có phương trình y2 = 8x.
Lời giải:
Giả sử parabol (P) có phương trình chính tắc là y2 = 2px (p > 0).
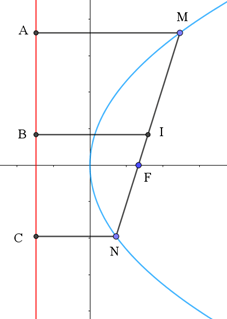
Gọi A, B, C lần lượt là hình chiếu của M, I, N lên Δ.
Vì I là trung điểm của MN nên IB là đường trung bình của hình thang MACN
⇒IB=12(MA+CN)=12(MF+CF)=12MN.
⇒ Đường tròn đường kính MN chính là đường tròn tâm I, bán kính IB
Lại có Δ vuông góc với IB tại B
⇒ đường tròn đường kính MN tiếp xúc với Δ tại B.
Lời giải:
Giả sử parabol (P) có phương trình chính tắc là y2 = 2px (p > 0).
Gọi toạ độ của M là (x; y).
F(p2;0) là tiêu điểm của (P), H là hình chiếu của M lên đường chuẩn Δ: x+p2=0 của (P).
Khi đó:
MF = √(p2-x)2+y2=√p24-px+x2+2px=√p24+px+x2=√(x+p2)2=|x+p2|.
MH = |x+p2|.
Vậy MF = MH, mặt khác MH chính là bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P), do đó bán kính qua tiêu của điểm M trên parabol (P) bằng bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P).
a) Viết phương trình chính tắc của parabol (P).
b) Tính khoảng cách giữa sao chổi A và tâm Mặt Trời khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).
Lời giải:
a) Chọn hệ trục toạ độ sao cho gốc toạ độ O trùng với đỉnh của parabol, tâm Mặt Trời trùng với tiêu điểm của parabol, đơn vị trên các trục là kilômét.
Gọi phương trình chính tắc của (P) là y2 = 2px (p > 0).
Gọi F là tiêu điêm của (P), (x; y) là toạ độ của sao chổi A.
Khi đó khoảng cách giữa sao chổi A và tâm Mặt Trời là AF = x+p2 ≥ p2 (vì x ≥ 0)
⇒ khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là p2 (km)
⇒p2=112⇒p=224.
Vậy phương trình chính tắc của (P) là y2 = 448x.
b) Khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P) thì sao chổi có hoành độ là x=p2.
Khoảng cách giữa sao chổi A và tâm Mặt Trời khi đó là:
AF = x+p2=p2+p2=p=224 (km).
Lời giải:
Có 2p = 6, suy ra p = 3.
Khoảng cách từ điểm M(1;√6) trên gương đến tiêu điểm của (P) là:
MF = x+p2=1+32=52=2,5(cm).
Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 8: Tính chất chung của ba đường conic
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.