Toptailieu.vn giới thiệu giải bài tập Chuyên đề Toán 10 Bài 8: Tính chất chung của ba đường conic sách Chân trời sáng tạo hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề học tập Toán 10. Mời các bạn đón xem:

Giải bài tập Chuyên đề Toán 10 Bài 8: Tính chất chung của ba đường conic

1. Giao của mặt phẳng với mặt nón tròn xoay

Khám phá 1 trang 60 Chuyên đề Toán 10: Gắn một đoạn ống nhựa vào đầu bóng của một đèn chiếu nhỏ để tạo ra một chùm ánh sáng hình mặt nón tròn xoay (Hình 1a, b). Chiếu đèn lên một bức tường với các góc nghiêng khác nhau để ánh sáng từ đèn hắt lên bức tường tạo thành các bóng khác nhau (Hình 1c, d, e). Nhận xét hình ảnh bạn nhìn thấy trên bức tường.

Lời giải:

Những hình ảnh ta thấy trong các Hình 1c, 1d và 1e lần lượt là elip, hypebol và parabol.

Thực hành 1 trang 61 Chuyên đề Toán 10: Giao của mặt phẳng và mặt nón trong Hình 2b, c có dạng đường gì?

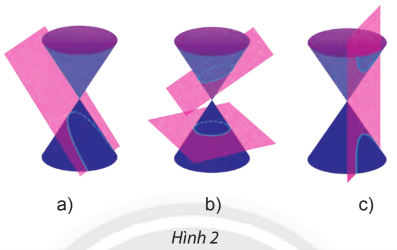
Lời giải:

– Trong Hình 2b, giao của mặt phẳng và mặt nón là một đường elip và một đường tròn.

– Trong Hình 2c, giao của mặt phẳng và mặt nón là một đường hypebol.

Vận dụng 1 trang 61 Chuyên đề Toán 10: Khi máy bay bay song song với mặt đất với vận tốc lớn hơn vận tốc của âm thanh sẽ tạo ra các lớp không khí dao động có hình mặt nón (nón Mach) (Hình 3) và tạo ra tiếng nổ mạnh, gọi là tiếng nổ siêu thanh. Những người trên mặt đất nếu nghe thấy tiếng nổ này cùng một thời điểm thì vị trí của họ cùng thuộc một đường hypebol. Hãy giải thích điều này.

Lời giải:

Vì máy bay bay song song với mặt đất nên giao của các lớp không khí dao động có hình mặt nón và mặt đất (mặt phẳng) là một đường hypebol. Do đó những người cùng đứng trên hypebol này sẽ nghe thấy tiếng nổ tại cùng thời điểm, và ngược lại, những người nghe thấy tiếng nổ này cùng một thời điểm thì họ cùng đứng trên đường hypebol này.

2. Xác định đường conic theo tâm sai, tiêu điểm và đường chuẩn

Khám phá 2 trang 61 Chuyên đề Toán 10: Cho đường conic có tiêu điểm F, đường chuẩn Δ và một điểm M là điểm nằm trên đường conic đó.

Tìm mối liên hệ giữa tỉ số $\frac{MF}{d(M;\mathrm{\Delta })}$ và tên gọi của đường conic.

Lời giải:

– Với elip, ta có $\frac{MF}{d(M;\mathrm{\Delta })}$ = e < 1.

– Với parabol, ta có $\frac{MF}{d(M;\mathrm{\Delta })}$ = e = 1.

– Với hypebol, ta có $\frac{MF}{d(M;\mathrm{\Delta })}$ = e > 1.

Thực hành 2 trang 63 Chuyên đề Toán 10: Xác định tâm sai, toạ độ một tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau

a) $\frac{x^2}{5}+\frac{y^2}{2}=1$;

b) $\frac{x^2}{12}-\frac{y^2}{4}=1$;

c) $y^2=\frac{1}{2}x$.

Lời giải:

a) Đây là một elip.

Có a² = 5, b² = 2 $\Rightarrow a=\sqrt{5},b=\sqrt{2},c=\sqrt{a^2-b^2}=\sqrt{5-2}=\sqrt{3},$

e = $\frac{c}{a}=\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5},\frac{a}{e}=\frac{\sqrt{5}}{\frac{\sqrt{15}}{5}}=\frac{5\sqrt{3}}{3}.$

Suy ra elip có tiêu điểm F₁$(-\sqrt{3};0)$, đường chuẩn Δ₁: x = $-\frac{5\sqrt{3}}{3}$ và tâm sai e = $\frac{\sqrt{15}}{5}.$

b) Đây là một hypebol.

Có a² = 12, b² = 4 $\Rightarrow a=2\sqrt{3},b=2,c=\sqrt{a^2+b^2}=\sqrt{12+4}=\sqrt{16}=4,$

e = $\frac{c}{a}=\frac{4}{2\sqrt{3}}=\frac{2\sqrt{3}}{3},\frac{a}{e}=\frac{2\sqrt{3}}{\frac{2\sqrt{3}}{3}}=3.$

Suy ra hypebol có tiêu điểm F₁(-4;0), đường chuẩn Δ₁: x = –3 và tâm sai e = $\frac{2\sqrt{3}}{3}.$

c) Đây là một parabol.

CÓ 2p = $\frac{1}{2}$, suy ra p = $\frac{1}{4}$

Suy ra parabol có tiêu điểm F$(\frac{1}{8};0),$ đường chuẩn Δ: $x=-\frac{1}{8}$ và tâm sai e = 1.

Vận dụng 2 trang 64 Chuyên đề Toán 10: Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol?

Lời giải:

Vì quỹ đạo của Trái Đất có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo của Sao chổi Halley có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo của Sao chổi Great Southern of 1887 có tâm sai bằng 1 nên là đường parabol.

Vì quỹ đạo của Vật thể Oumuamua có tâm sai lớn hơn 1 nên là đường hypebol.

Bài 1 trang 64 Chuyên đề Toán 10: Xác định tâm sai, toạ độ một tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:

a) $\frac{x^2}{9}+\frac{y^2}{7}=1$;

b) $\frac{x^2}{15}-\frac{y^2}{10}=1$;

c) y² = x.

Lời giải:

a) Đây là một elip.

Có a² = 9, b² = 7 $\Rightarrow a=3,b=\sqrt{7},c=\sqrt{a^2-b^2}=\sqrt{9-7}=\sqrt{2},$

e = $\frac{c}{a}=\frac{\sqrt{2}}{3},\frac{a}{e}=\frac{3}{\frac{\sqrt{2}}{3}}=\frac{9\sqrt{2}}{2}.$

Suy ra elip có tiêu điểm F₁$(-\sqrt{2};0)$, đường chuẩn Δ₁: x = $-\frac{9\sqrt{2}}{2}$ và tâm sai e = $\frac{\sqrt{2}}{3}.$

b) Đây là một hypebol.

Có a² = 15, b² = 10 $\Rightarrow a=\sqrt{15},b=\sqrt{10},c=\sqrt{a^2+b^2}=\sqrt{15+10}=\sqrt{25}=5,$

e = $\frac{c}{a}=\frac{5}{\sqrt{15}}=\frac{\sqrt{15}}{3},\frac{a}{e}=\frac{\sqrt{15}}{\frac{\sqrt{15}}{3}}=3.$

Suy ra hypebol có tiêu điểm F₁(–5; 0), đường chuẩn Δ₁: x = –3 và tâm sai e = $\frac{\sqrt{15}}{3}.$

c) Đây là một parabol.

CÓ 2p = 1, suy ra p = $\frac{1}{2}$

Suy ra parabol có tiêu điểm F$(\frac{1}{4};0),$ đường chuẩn Δ: $x=-\frac{1}{4}$ và tâm sai e = 1.

Bài 2 trang 64 Chuyên đề Toán 10: Viết phương trình của conic có tâm sai e = 1, tiêu điểm F(1; 0) và đường chuẩn Δ: x + 1 = 0

Lời giải:

Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có: $\frac{MF}{d(M;\mathrm{\Delta })}=e$

$\iff \frac{\sqrt{{(1-x)}^2+{(0-y)}^2}}{|x+1|}=1$

$\iff \sqrt{{(1-x)}^2+{(0-y)}^2}=|x+1|$

$\iff {(1-x)}^2+{(0-y)}^2={|x+1|}^2$

$\iff (1-2x+x^2)+y^2=x^2+2x+1$

$\iff y^2=4x.$

Vậy phương trình của conic đã cho là y² = 4x.

Bài 3 trang 64 Chuyên đề Toán 10: Viết phương trình của conic (C) trong mỗi trường hợp sau:

a) (C) có tiêu điểm F(8; 0), đường chuẩn Δ: x – 2 = 0 và tâm sai e = 2;

b) (C) có tiêu điểm F(–4; 0), đường chuẩn $\mathrm{\Delta }:x+\frac{25}{4}=0$ và tâm sai $e=\frac{4}{5}.$

Lời giải:

a) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có: $\frac{MF}{d(M;\mathrm{\Delta })}=e$

$\iff \frac{\sqrt{{(8-x)}^2+{(0-y)}^2}}{|x-2|}=2$

$\iff \sqrt{{(8-x)}^2+{(0-y)}^2}=2|x-2|$

$\iff {(8-x)}^2+{(0-y)}^2=4{|x-2|}^2$

$\iff (64-16x+x^2)+y^2=4(x^2-4x+4)$

$\iff 3x^2-y^2=48$

$\iff \frac{x^2}{16}-\frac{y^2}{48}=1.$

Vậy phương trình của conic đã cho là $\frac{x^2}{16}-\frac{y^2}{48}=1.$

b) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có: $\frac{MF}{d(M;\mathrm{\Delta })}=e$

$\iff \frac{\sqrt{{(-4-x)}^2+{(0-y)}^2}}{|x+\frac{25}{4}|}=\frac{4}{5}$

$\iff \sqrt{{(-4-x)}^2+{(0-y)}^2}=\frac{4}{5}|x+\frac{25}{4}|$

$\iff {(-4-x)}^2+{(0-y)}^2=\frac{16}{25}{|x+\frac{25}{4}|}^2$

$\iff (16+8x+x^2)+y^2=\frac{16}{25}(x^2+\frac{25}{2}x+\frac{625}{16})$

$\iff 16+8x+x^2+y^2=\frac{16}{25}{x}^2+8x+25$

$\iff \frac{9}{25}{x}^2+y^2=9$

$\iff \frac{x^2}{25}+\frac{y^2}{9}=1.$

Vậy phương trình của conic đã cho là $\frac{x^2}{25}+\frac{y^2}{9}=1.$

Bài 4 trang 64 Chuyên đề Toán 10: Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol?

Lời giải:

Vì quỹ đạo của Sao Hoả có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo của Mặt Trăng có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo của Sao Thuỷ có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo của Sao chổi Ikeya-Seki có tâm sai nhỏ hơn 1 nên là đường elip.

Vì quỹ đạo C/2019 Q4 có tâm sai lớn hơn 1 nên là đường hypebol.

Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 7: Parabol

Bài tập cuối chuyên đề 3

Bài 1: Hệ phương trình bậc nhất ba ẩn

Bài 2: Ứng dụng hệ phương trình bậc nhất ba ẩn

Bài tập cuối chuyên đề 1