Toptailieu.vn giới thiệu giải bài tập Chuyên đề Toán 10 Bài tập cuối chuyên đề 1 sách Chân trời sáng tạo hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề học tập Toán 10. Mời các bạn đón xem:

Giải bài tập Chuyên đề Toán 10 Bài tập cuối chuyên đề 1

Bài 1 trang 24 Chuyên đề Toán 10: Trong các hệ phương trình sau, hệ nào là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số (–1; 0; 1), $(\frac{1}{2};-\frac{1}{2};-1)$có là nghiệm của các hệ phương trình bậc nhất ba ẩn đó không?

$\mathrm{a)}\left\{\begin{array}{l}2x-y +z=-1\\ -x+2y=1\\ 3y-2z=-2\end{array}\right.$

$\mathrm{b)}\left\{\begin{array}{l}4x-2y+z=2\\ 8x+3z=1\\ -6y+2z=1\end{array}\right.$

$\mathrm{c)}\left\{\begin{array}{l}3x-2y+zx=2\\ xy-y+2z=1\\ x+2y-3yz=-2\end{array}\right.$

Lời giải:

a) và b) là các hệ phương trình bậc nhất ba ẩn; bc không phải hê phương trình bậc nhất ba ẩn vì chứa yz.

+) Bộ ba số (–1; 0; 1) có là nghiệm của hệ a).

Vì khi thay bộ số này vào từng phương trình thì chúng đều có nghiệm đúng:

2 . (–1) – 0 + 1 = –1;

–(–1) + 2 . 0 = 1;

3 . 0 – 2 . 1 = –2.

+) Bộ ba số $(\frac{1}{2};-\frac{1}{2};-1)$không là nghiệm của hệ a).

Vì khi thay bộ số này vào phương trình thứ nhất của hệ ta được $2.\frac{1}{2}-(-\frac{1}{2})+(-1)=-1,$ đây là đẳng thức sai.

+) Bộ ba số (–1; 0; 1) không là nghiệm của hệ b).

Vì khi thay bộ số này vào phương trình thứ nhất của hệ ta được 4 . (–1) – 2 . 0 + 1 = 2, đây là đẳng thức sai.

+) Bộ ba số $(\frac{1}{2};-\frac{1}{2};-1)$có là nghiệm của hệ b).

Vì khi thay bộ số này vào từng phương trình thì chúng đều có nghiệm đúng:

$4.\frac{1}{2}-2(-\frac{1}{2})+(-1)=2;$

$8.\frac{1}{2}+3.(-1)=1;$

$-6(-\frac{1}{2})+2.(-1)=1.$

Bài 2 trang 24 Chuyên đề Toán 10: Giải các hệ phương trình sau bằng phương pháp Gauss:

a) $\left\{\begin{array}{l}x-2y+z=3\\ -y+z=2\\ y+2z=1;\end{array}\right.$

b) $\left\{\begin{array}{l}3x-2y-4z=3\\ 4x+6y-z=17\\ x+2y=5\end{array}\right.$

c)$\left\{\begin{array}{l}x+y+z=1\\ 3x-y-z=4\\ x+5y+5z=-1\end{array}\right.$

Lời giải:

a) $\left\{\begin{array}{l}x-2y+z=3\\ -y+z=2\\ y+2z=1\end{array}\right.\iff \left\{\begin{array}{l}x-2y+z=3\\ -y+z=2\\ 3z=3\end{array}\right.\iff \left\{\begin{array}{l}x-2y+z=3\\ -y+1=2\\ z=1\end{array}\right.\iff \left\{\begin{array}{l}x-2.(-1)+1=3\\ y=-1\\ z=1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=0\\ y=-1\\ z=1\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm duy nhất (0; –1; 1).

b)$$\begin{gathered} \left\{\begin{array}{l}3x-2y-4z = 3\\ 4x+6y-z =17\\ x+2y =5\end{array}\right.\iff \left\{\begin{array}{l}3x-2y-4z = 3\\ -13x-26y =-65\\ x+2y =5\end{array}\right.\iff \left\{\begin{array}{l}3x-2y-4z = 3\\ x+2y =5\\ x+2y =5\end{array}\right. \\ \iff \left\{\begin{array}{l}3x-2y-4z = 3\\ x+2y =5\end{array}\right. \end{gathered}$$

Từ phương trình thứ hai ta có x = –2y + 5, thay vào phương trình thứ nhất ta được z = –2y + 3. Vậy hệ phương trình đã cho có vô số nghiệm dạng (–2y + 5; y; –2y + 3).

c) $\left\{\begin{array}{l}x+y+z=1\\ 3x-y-z=4\\ x+5y+5z=-1\end{array}\right.\iff \left\{\begin{array}{l}x+y+z=1\\ 4y+4z=-1\\ x+5y+5z=-1\end{array}\right.\iff \left\{\begin{array}{l}x+y+z=1\\ 4y+4z=-1\\ -4y-4z=2\end{array}\right.\iff \left\{\begin{array}{l}x+y+z=1\\ 4y+4z=-1\\ 0y+0z=1\end{array}\right.$

Vì phương trình thứ ba của hệ vô nghiệm nên hệ đã cho vô nghiệm.

Bài 3 trang 24 Chuyên đề Toán 10: Tìm phương trình của parabol (P): y = ax2 + bx + c (a ≠ 0), biết:

a) Parabol (P) cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x = –2; x = 1 và đi qua điểm M(–1; 3);

b) Parabol (P) cắt trục tung tại điểm có tung độ y = –2 và hàm số đạt giá trị nhỏ nhất bằng –4 tại x = 2.

Lời giải:

a) (P) cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x = –2; x = 1

$\Rightarrow \left\{\begin{array}{l}0=a{(-2)}^2+b(-2)+c\\ 0=a.1^2+b.1+c\end{array}\right.\Rightarrow \left\{\begin{array}{l}4a-2b+c=0 \left(1\right)\\ a+b+c=0 \hspace{0.17em}\left(2\right)\end{array}\right.$

(P) đi qua điểm M(–1; 3) M(-1;3) $\Rightarrow$ 3 = a(–1)2 + b(–1) + c $\Rightarrow$ a – b + c = 3 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}4a-2b+c=0\\ a+b+c=0\\ a-b+c=3\end{array}\right.$

Giải hệ này ta được a = $-\frac{3}{2}$, b = $-\frac{3}{2}$, c = 3.

Vậy phương trình của (P) là y = $-\frac{3}{2}{x}^2-\frac{3}{2}x+3.$

b) (P) cắt trục tung tại điểm có tung độ y = –2 $\Rightarrow$ –2 = a . 02 + b . 0 + c hay c = –2 (1).

Hàm số đạt giá trị nhỏ nhất bằng –4 tại x = 2

$\Rightarrow \left\{\begin{array}{l}-\frac{b}{2a}=2\\ -4=a.2^2+b.2+c\end{array}\right.\Rightarrow \left\{\begin{array}{l}4a+b=0 \left(2\right)\\ 4a+2b+c=-4 \left(3\right)\end{array}\right.$

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}c=-2\\ 4a+b=0\\ 4a+2b+c=-4\end{array}\right.$

Giải hệ này ta được a = $\frac{1}{2}$, b = –2, c = –2.

Vậy phương trình của (P) là y = $\frac{1}{2}$x2 – 2x – 2.

Bài 4 trang 24 Chuyên đề Toán 10: Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích. Còn bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích. Biết giá tiền của bộ ba viên ngọc này là 270 triệu đồng. Tính giá tiền mỗi viên ngọc.

Lời giải:

Gọi giá tiễn mỗi viên ngọc lam, hoàng ngọc, ngọc bích lần lượt là x, y, z (triệu đồng).

Theo đề bài ta có:

– Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích, suy ra x + 2y = 3z hay x + 2y –3z = 0 (1).

– Bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích, suy ra 7x + y = 8z hay 7x + y – 8z = 0 (2).

– Giá tiền của bộ ba viên ngọc là 270 triệu đồng, suy ra x + y + z = 270 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+2y-3z=270\\ 7x+y-8z=0\\ x+y+z=270\end{array}\right.$

Giải hệ này ta được x = 90, y = 90, z = 90.

Vậy giá tiền mỗi viên ngọc đều là 90 triệu đồng.

Bài 5 trang 24 Chuyên đề Toán 10: Bốn ngư dân góp vốn mua chung một chiếc thuyền. Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại. Người thứ hai đóng góp bằng  tổng số tiền của những người còn lại. Người thứ ba đóng góp bằng  tổng số tiền của những người còn lại. Người thứ tư đóng góp 130 triệu đồng. Chiếc thuyền này được mua giá bao nhiêu?

Lời giải:

Gọi số tiền người thứ nhất, người thứ hai, người thứ ba đóng góp lần lượt là x, y,z (triệu đồng).

Theo đề bài ta có:

– Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại, suy ra x = $\frac{1}{2}$(y + z + 130) hay 2x – y – z = 130 (1).

– Người thứ hai đóng góp bằng $\frac{1}{3}$ tổng số tiền của những người còn lại, suy ra y = $\frac{1}{3}$(x + z + 130) hay –x + 3y – z = 130 (2).

– Người thứ ba đóng góp bằng $\frac{1}{4}$ tổng số tiền của những người còn lại, suy ra z = $\frac{1}{4}$(x + y + 130) hay –x – y + 4z = 130 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}2x-y-z=130\\ -x+3y-z=130\\ -x-y+4z=130\end{array}\right.$

Giải hệ này ta được x = 200, y = 150, z = 120.

Suy ra tổng số tiền là: 200 + 150 + 120 + 130 = 600 (triệu đồng).

Vậy chiếc thuyền này được mua giá 600 triệu đồng.

Bài 6 trang 24 Chuyên đề Toán 10: Một quỹ đầu tư dự kiến dành khoản tiền 1,2 tỉ đồng để đầu tư vào cồ phiếu. Để thấy được mức độ rủi ro, các cổ phiếu được phân thành ba loại: rủi ro cao, rủi ro trung bình và rủi ro thấp. Ban Giám đốc của quỹ ước tính các cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp sẽ có lợi nhuận hằng năm lần lượt là 15%, 10% và 6%. Nếu đặt ra mục tiêu đầu tư có lợi nhuận trung bình là 9%/năm trên tổng số vốn đầu tư, thì quỹ nên đầu tư bao nhiêu tiền vào mỗi loại cổ phiếu? Biết rằng, để an toàn, khoản đầu tư vào các cổ phiếu rủi ro thấp sẽ gấp đôi tổng các khoản đầu tư vào các cổ phiếu thuộc hai loại còn lại.

Lời giải:

Gọi số tiền nên đầu tư vào mỗi loại cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp lần lượt là x, y, z (tỉ đồng).

Theo đề bài ta có:

– Tổng số tiền đầu tư là 1,2 tỉ, suy ra x + y + z = 1,2 (1).

– Mục tiêu đầu tư có lợi nhuận trung bình là 9%/năm trên tổng số vốn đầu tư, suy ra 15%x + 10%y + 6%z = 9% . 1,2 hay 15x + 10y + 6z = 10,8 (2).

– Khoản đầu tư vào các cổ phiếu rủi ro thấp sẽ gấp đôi tổng các khoản đầu tư vào các cổ phiếu thuộc hai loại còn lại, suy ra z = 2(x + y) hay 2x + 2y – z = 0 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=1,2\\ 15x+10y+6z=10,8\\ 2x+2y-z=0\end{array}\right.$

Giải hệ này ta được x = 0,4, y = 0, z = 0,8.

Vậy số tiền nên đầu tư vào mỗi loại cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp lần lượt là 0,4 tỉ đồng, 0 đồng, 0,8 tỉ đồng.

Bài 7 trang 24 Chuyên đề Toán 10: Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,5 và tổng số tế bào con tạo ra là 216. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại B được tạo ra ít hơn số tế bào con loại C được tạo ra là 40. Tính số tế bào con mỗi loại lúc ban đầu.

Lời giải:

Gọi số tế bào con ban đầu mỗi loại A, B, C lần lượt là x, y, z.

Theo đề bài ta có:

– Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,5. Suy ra số tế bào con mỗi loại A, B, C lần lượt là 23x, 24y, 25z hay 8x, 16y, 32z.

– Tổng số tế bào con tạo ra là 216, suy ra 8x + 16y + 32z = 216 hay x + 2y + 4z = 27 (1).

– Khi chưa thực hiện nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B, suy ra z = $\frac{1}{2}$(x + y) hay x + y – 2z = 0 (2).

– Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại B được tạo ra ít hơn số tế bào con loại C được tạo ra là 40, suy ra 8x + 16y = 32z – 40 hay x + 2y – 4z = –5 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+2y+4z=27\\ x+y-2z=0\\ x+2y-4z=-5\end{array}\right.$

Giải hệ này ta được x = 5, y = 3, z = 4.

Vậy số tế bào con ban đầu mỗi loại A, B, C lần lượt là 5, 3, 4.

Bài 8 trang 25 Chuyên đề Toán 10: Cho sơ đồ mạch điện như Hình 1. Biết rằng R = R1 = R2 = 5 Ω. Hãy tính các cường độ dòng điện I, I1 và I2

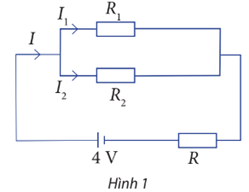
Lời giải:

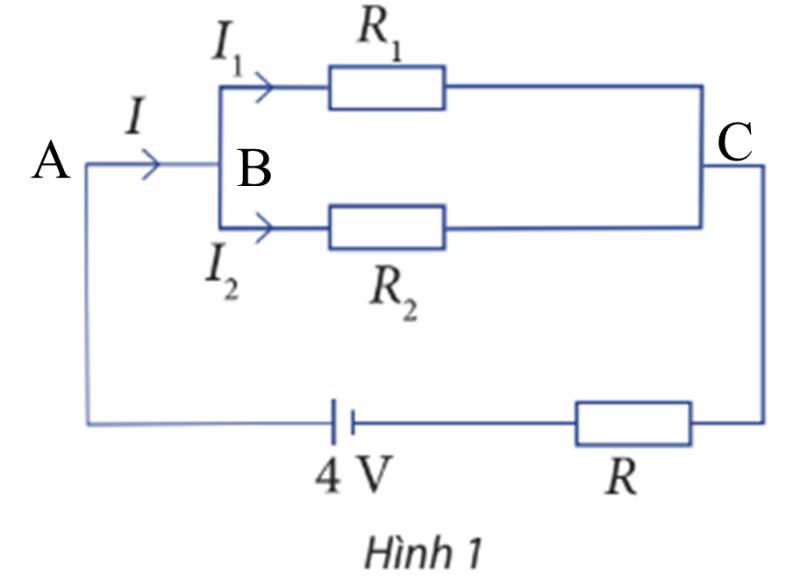
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau nên ta có I = I1 + I2 (1).

Hiệu điện thế giữa hai điểm A và C được tính bởi:

UAC = IR + I1R1 = 5I + 5I1, suy ra 5I + 5I1 = 4 (2).

Hiệu điện thế giữa hai điểm B và C được tính bởi:

UBC = I1R1 = I2R2, suy ra 5I1 = 5I2 hay I1 = I2 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}I-I_1-I_2=\mathrm{0\hspace{0.25em}5}\\ 5I+5I_1=4\\ I_1-I_2=0\end{array}\right.$

Giải hệ này ta được $I=\frac{8}{15},I_1=\frac{4}{15},I_2=\frac{4}{15}.$

Bài 9 trang 25 Chuyên đề Toán 10: Cho A, B và C là ba dung dịch cùng loại acid có nồng độ khác nhau. Biết rằng nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M (mol/lít); nếu trộn 100 ml dung dịch A với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M; nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M. Mỗi dung dịch A, B và C có nồng độ bao nhiêu?

Lời giải:

Gọi nồng độ của mỗi dung dịch A, B, C lần lượt là x, y, z (M).

Theo đề bài ta có:

– Nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M, suy ra $\frac{0,1x+0,1y+0,1z}{0,1+0,1+0,1}$ = 0,4 hay x + y + z = 1,2 (1).

– Nếu trộn 100 ml dung dịch A với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M, suy ra $\frac{0,1x+0,2y}{0,1+0,2}$ = 0,6 hay x + 2y = 1,8 (2).

– Nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M, suy ra $\frac{0,1y+0,2z}{0,1+0,2}$ = 0,3 hay y + 2z = 0,9 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=1,2\\ x+2y=1,8\\ y+2z=0,9\end{array}\right.$

Giải hệ này ta được x = 0,4; y = 0,7; z = 0,1.

Vậy nồng độ của mỗi dung dịch A, B, C lần lượt là 0,4 M; 0,7 M; 0,1 M.

Bài 10 trang 25 Chuyên đề Toán 10: Xăng sinh học E5 là hỗn hợp xăng không chì truyền thống và cồn sinh học (bio – ethanol). Trong loại xăng này chứa 5% cồn sinh học. Khi động cơ đốt cháy lượng cồn trên thì xảy ra phản ứng hoá học

C2H6O + O2 $\stackrel{{\mathrm{t}}^{°}}{\to }$ CO2 + H2O.

Cân bằng phương trình hoá học trên.

Lời giải:

Gọi x, y, z, t lần lượt là bốn số nguyên dương thoả mãn cân bằng phương trình phản ứng hoá học:

xC2H6O + yO2 $\stackrel{{\mathrm{t}}^{°}}{\to }$ zCO2 + tH2O.

Số nguyên tử C ở hai vế bằng nhau, ta có 2x = z (1).

Số nguyên từ H ở hai vế bằng nhau, ta có 6x = 2t hay 3x = t (2).

Số nguyên từ O ở hai vế bằng nhau, ta có x + 2y = 2z + t (3).

Thay (1) và (2) vào (3) ta được x + 2y = 2 . 2x + 3x hay y = 3x.

Vậy y = 3x, z = 2x, t = 3x.

Để phương trình có hệ số đơn giản, ta chọn x = 1, khi đó y = 3, z = 2, t = 3.

Vậy phương trình cân bằng phản ứng hoá học là C2H6O + 3O2 $\stackrel{\mathrm{t}°}{\to }$ 2CO2 + 3H2O.

Bài 11 trang 25 Chuyên đề Toán 10: Trên thị trường hàng hoá có ba loại sản phẩm A, B, C với giá mỗi tấn tương ứng là x, y, z (đơn vị: triệu đồng, x ≥ 0, y ≥ 0, z ≥ 0). Lượng cung và lượng cầu của mỗi sản phẩm được cho trong bảng dưới đây:

Tìm giá của mỗi sản phẩm để thị trường cân bằng.

Lời giải:

Thị trường cân bằng khi $\left\{\begin{array}{l}{Q}_{S_A}=Q_{D_A}\\ Q_{S_B}=Q_{D_B}\\ \begin{array}{c}{Q}_{S_C}=Q_{D_C}\end{array}\end{array}\right.$

$\iff \left\{\begin{array}{l}-60+4x-2z=137-3x+y\\ -30-x+5y-z=131+x-4y+z\\ \begin{array}{c}-30-2x+3z=157+y-2z\end{array}\end{array}\right.\iff \left\{\begin{array}{l}7x-y-2z=197\\ 2x-9y+2z=-161\\ \begin{array}{c}2x+y-5z=-187\end{array}\end{array}\right.\iff \left\{\begin{array}{l}x=54\\ y=45\\ z=68\end{array}\right.$

Vậy giá mỗi mỗi sản phẩm A, B, C lần lượt là 54, 45 và 68 triệu đồng.

Bài 12 trang 25 Chuyên đề Toán 10: Giải bài toán cổ sau:

Trăm trâu, trăm cỏ

Trâu đứng ăn năm

Trâu nằm ăn ba

Lụ khụ trâu già

Ba con một bó

Hỏi có bao nhiêu con trâu đứng, trâu nằm, trâu già?

Lời giải:

Gọi số trâu đứng, trâu nằm, trâu già lần lượt là x, y, z (x, y, z là số nguyên dương).

Theo đề bài ta có hệ phương trình: $\left\{\begin{array}{l}x+y+z=100\\ 5x+3y+\frac{1}{3}z=100\end{array}\right.(*).$

(*) $\iff \left\{\begin{array}{l}x+y=100-z\\ 15x+9y=300-z\end{array}\iff \left\{\begin{array}{l}x=\frac{-300+4z}{3}\\ y=\frac{600-7z}{3}\end{array}\right.\right.\iff \left\{\begin{array}{l}x=\frac{4z}{3}-100\\ \begin{array}{c}y=200-\frac{7z}{3}\end{array}.\end{array}\right.$

Vìx > 0 nên $\frac{4z}{3}-100>0 \Rightarrow z>75,$

y > 0 nên $200-\frac{7z}{3}>0\Rightarrow z<85.$

Mà z là số nguyên dương nên $z\in \{76;77;\mathrm{\dots };84\}.$

Lại có x là số nguyên nên $\frac{4z}{3}-100$ là số nguyên, suy ra z ⁝ 3 $\Rightarrow z\in \{78;81;84\}.$

+) Với z = 78 thì x = 4, y = 18.

+) Với z = 81 thì x = 8, y = 11.

+) Với z = 84 thì x = 12, y = 4.

Vậy số trâu đứng, trâu nằm, trâu già theo thứ tự có thể là một trong ba bộ số (4; 18; 78), (8; 11; 81), (12; 4; 84).

Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Ứng dụng hệ phương trình bậc nhất ba ẩn

Bài 3: Phương pháp quy nạp toán học

Bài 4: Nhị thức Newton

Bài tập cuối chuyên đề 2

Bài 5: Elip