Toptailieu.vn giới thiệu giải bài tập Chuyên đề Toán 10 Bài 5: Elip sách Chân trời sáng tạo hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề học tập Toán 10. Mời các bạn đón xem:
Giải bài tập Chuyên đề Toán 10 Bài 5: Elip
1. Tính đối xứng của elip
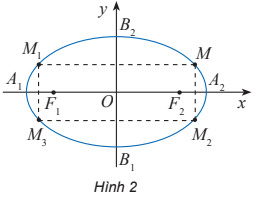
Các điểm M1(–x0; y0), M2(x0; –y0), M3(–x0; –y0) có thuộc (E) hay không?
Lời giải:
Nếu điểm M(x0; y0) thuộc (E) thì ta có:
Ta có: nên các điểm có toạ độ M1(x0; –y0), M2(–x0; y0), M3(–x0; –y0) cũng thuộc (E).
Lời giải:
Gọi phương trình chính tắc của elip đã cho là (a > b > 0).
Theo đề bài ta có: elip có kích thước của hình chữ nhật cơ sở là 8 và 6 2a = 8 và 2b = 6 a = 4, b = 3
Toạ độ các đỉnh của elip là A1(–4; 0), A2(4; 0), B1(0; –3), B2(0; 3).
Toạ độ các tiêu điểm của elip là F1(–; 0), F2(; 0).
Tiêu cự của elip là 2c = 2.
Độ dài trục lớn là 2a = 8, độ dài trục bé là 2b = 6.
Lời giải:
Đầu tiên gấp tờ giấy sao cho hai đỉnh đối diện của elip trùng nhau.
Khi đó đường gấp sẽ đi qua hai đỉnh còn lại của elip, gấp tiếp tờ giấy sao cho hai đỉnh còn lại này trùng nhau. Khi đó ta đã gấp elip thành 4 phần chồng khít lên nhau.
2. Bán kính qua tiêu
a) Tính F1M2 và F2M2 theo x, y, c.
b) Chứng tỏ rằng: F1M2 – F2M2 = 4cx, F1M – F2M =
c) Tính độ dài hai đoạn MF1 và MF2 theo a, c, x.
Lời giải:
a) F1M2 = [x – (– c)]2 + (y – 0)2 = (x + c)2 + y2 = x2 + 2cx + c2 + y2;
F2M2 = (x – c)2 + (y – 0)2 = x2 – 2cx + c2 + y2.
b) F1M2 – F2M2 = (x2 + 2cx + c2 + y2) – (x2 – 2cx + c2 + y2) = 4cx.
F1M2 – F2M2 = 4cx (F1M + F2M)(F1M – F2M) = 4cx 2a(F1M – F2M) = 4cx
F1M – F2M = = .
c)
+) Từ F1M + F2M = 2a và ta suy ra:
(F1M + F2M) + (F1M – F2M) = 2a + 2F1M = 2a + MF1 = a + x.
+) Từ F1M + F2M = 2a và ta suy ra:
(F1M + F2M) – (F1M – F2M) = 2a – 2F2M = 2a – MF2 = a – x.
Thực hành 2 trang 44 Chuyên đề Toán 10:
a) Tính độ dài hai bán kính qua tiêu của điểm M(x; y) trên elip (E):
b) Tìm các điểm trên elip có độ dài hai bán kính qua tiêu bằng nhau.
Lời giải:
a) Có a2 = 64, b2 = 36 a = 8, b = 6
Độ dài hai bán kính qua tiêu của M(x; y) là:
MF1 = a + x = 8 + = 8 + ; MF2 = a – x = 8 – = 8 –
b) Giả sử M(x; y) nằm trên (E) thoả mãn đề bài. Khi đó:
MF1 = MF2 8 + = 8 – x = 0
Vậy có hai điểm thoả mãn đề bài là M1(0; 6) và M2(0; –6).
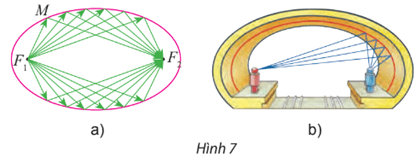
Vòm xe điện ngầm của một thành phố có mặt cắt hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
Lời giải:
Vì âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu nên quãng đường âm thanh đã đi là MF1 + MF2.
Mà MF1 + MF2 = (a + x) + (a – x) = 2a nên quãng đường âm thanh đi luôn không đổi dù đến các điểm khác nhau trên elip, vận tốc âm thanh cũng không đổi nên thời gian âm thanh đã đi cũng không đổi. Do đó âm thanh khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.
3. Tâm sai
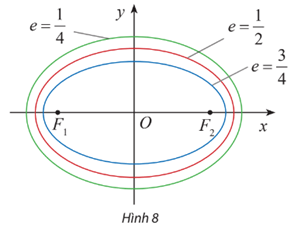
Khám phá 3 trang 45 Chuyên đề Toán 10: Cho biết ti số của các elip lần lượt là (Hình 8)
Lời giải:
Ta có . Nhận xét:
– Khi tâm sai e càng bé (tức là càng gần 0) thì b càng gần a và elip trông càng "béo".
– Khi tâm sai e càng lớn (tức là càng gần 1) thì tỉ số càng gần 0 và elip trông càng "dẹt".
Thực hành 3 trang 45 Chuyên đề Toán 10:
a) Tìm tâm sai của elip (E): và elip
b) Không cần vẽ hình, theo bạn elip nào có hình dạng "dẹt" hơn?
Lời giải:
Có
a) Tâm sai của (E) là e =
tâm sai của (E') là e' =
b) Vì (E') có tâm sai lớn hơn tâm sai của (E) nên (E') có hình dạng "dẹt" hơn.
(Nguồn: https://www.nasa.gov)
Lời giải:
Nhìn hình ta thấy quỹ đạo chuyển động của tiểu hành tinh HD20782b "dẹt" hơn so với quỹ đạo chuyển động của Trái Đất, do đó tâm sai của quỹ đạo chuyển động của Trái Đất nhỏ hơn tâm sai của quỹ đạo chuyển động của tiểu hành tinh HD20782b.
4. Đường chuẩn
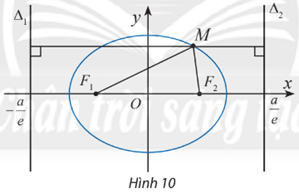
Dựa theo cách tính trên, hãy tính .
Lời giải:
Có a – ex = MF2 > 0 nên a – ex > 0.
(vì a – ex > 0).
a) ;
b) .
Lời giải:
a) Có a2 = 4, b2 = 1 a = 2, b = 1
Toạ độ hai tiêu điểm của elip là và
Phương trình đường chuẩn ứng với tiêu điểm F1 là
Δ1:
Phương trình đường chuẩn ứng với tiêu điểm F2 là
Δ2:
Lời giải:
Gọi phương trình chính tắc của elip đã cho là (a > b > 0).
Theo đề bài ta có:
– Elip có tiêu cự bằng 6, suy ra 2c = 6, suy ra c = 3.
– Khoảng cách giữa hai đường chuẩn là , suy ra
Vậy phương trình chính tắc của elip đã cho là
Bài 1 trang 47 Chuyên đề Toán 10: Cho elip
a) Tìm tâm sai, chiều dài, chiều rộng hình chữ nhật cơ sở của (E) và vẽ (E).
b) Tìm độ dài hai bán kính qua tiêu của điểm M(0; 6) trên (E).
c) Tìm toạ độ hai tiêu điểm và viết phương trình hai đường chuẩn của (E).
Lời giải:
a) Có a2 = 64, b2 = 36 a = 8, b = 6
Tâm sai của (E) là
Chiều dài hình chữ nhật cơ sở là 2a = 16, chiều rộng hình chữ nhật cơ sở là 2b = 12.
Vẽ (E):
b) hai bán kính qua tiêu của điểm M(0; 6) là MF1 = a + = 8 + = 8,
MF2 = a – = 8 – = 8.
Lời giải:
Xét điểm M có toạ độ là (x; y).
+) Xét khoảng cách từ M đến F1.
Theo công thức độ dài bán kính qua tiêu ta có MF1 = a + x.
Mặt khác, vì M thuộc elip nên –a ≤ x ≤ a
Vậy a – c ≤ MF1 ≤ a + c.
Vậy độ dài MF1 nhỏ nhất bằng a – c khi M có hoành độ là –a, lớn nhất bằng a + c khi M có hoành độ bằng a.
+) Xét khoảng cách từ M đến F2.
Theo công thức độ dài bán kính qua tiêu ta có MF2 = a – x.
Mặt khác, vì M thuộc elip nên –a ≤ x ≤ a
Vậy a + c ≥ MF2 ≥ a – c.
Vậy độ dài MF2 nhỏ nhất bằng a – c khi M có hoành độ là a, lớn nhất bằng a + c khi M có hoành độ bằng –a.
Lời giải:
Gọi phương trình chính tắc của elip đã cho là (a > b > 0).
Theo đề bài ta có:
– Elip có tiêu cự bằng 12, suy ra 2c = 12, suy ra c = 6.
– Khoảng cách giữa hai đường chuẩn là , suy ra
Vậy phương trình chính tắc của elip đã cho là
Bài 4 trang 48 Chuyên đề Toán 10: Cho elip
a) Tìm tâm sai và độ dài hai bán kính qua tiêu của điểm M(3; 0) trên (E).
b) Tìm điểm N trên (E) sao cho NF1 = NF2.
c) Tìm điểm S trên (E) sao cho SF1 = 2SF2.
Lời giải:
a) Có a2 = 9, b2 = 1 a = 3, b = 1
Tâm sai của (E) là
Độ dài hai bán kính qua tiêu của điểm M(3; 0) là MF1 = a + = 3 + = 3 + , MF2 = a – = 3 – = 3 –
b) Gọi toạ độ của N là (x; y). Khi đó NF1 = a + x, NF2 = a – .
NF1 = NF2 a + = a – x = 0
Vậy có hai điểm N thoả mãn là N1(0; 1) và N2(0; –1).
c) Gọi toạ độ của S là (x; y). Khi đó SF1 = a + , SF2 = a – .
SF1 = 2SF2 a + = 2
Vậy có hai điểm S thoả mãn là và
(Nguồn: https://www.universetoday.com)
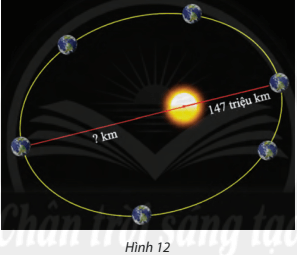
Lời giải:
Chọn hệ trục toạ độ sao cho tâm Mặt Trời trùng với tiêu điểm F1 của elip và trục Ox đi qua hai tiêu điểm của elip, đơn vị trên các trục toạ độ là triệu kilômét.
Khi đó phương trình của elip có dạng (a > b > 0).
Gọi toạ độ của Trái Đất là M(x; y) thì khoảng cách giữa tâm Trái Đất và tâm Mặt Trời là MF1 = a – ex ≥ a – ea (vì x ≤ a). Do đó khoảng cách gần nhất giữa Trái Đất và tâm Mặt Trơ là a – ea, suy ra a – ea = 147 a =
Mặt khác vì x ≥ –a nên a – ex ≤ a + ea nên khoảng cách xa nhất giữa Trái Đất và tâm Mặt Trời là a + ea = a(1 + e) = 152 (triệu km).
Vậy khoảng cách xa nhất giữa Trái Đất và tâm Mặt Trời là 152 triệu km.
(Nguồn: https://vi.wikipedia.org)
Lời giải:
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F1 của elip (E) và trục Ox đi qua hai tiêu điểm của elip, đơn vị trên các trục toạ độ là kilômét.
Khi đó phương trình của elip có dạng (a > b > 0).
Gọi toạ độ của Trái Đất là M(x; y) thì khoảng cách giữa vệ tinh và tâm Trái Đất là MF1 = a – ex.
Vì –a ≤ x ≤ a nên a – ea ≤ a –ex ≤ a + ea.
Do đó khoảng cách gần nhất giữa vệ tinh và tâm Trái Đất là a – ea và khoảng cách xa nhất giữa vệ tinh và tâm Trái Đất là a + ea
Cộng theo vế 2 phương trình này ta được 2a = 113896, suy ra a = 6948.
Thay vào phương trình thứ nhất ta được 6948 – 6948e = 6586 e ≈ 0,052.
Vậy tâm sai của quỹ đạo chuyển động của vệ tinh Sputnik I là 0,052.
Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.