Lời giải bài tập SBT Toán 10 Bài 24: Hoán vị, chỉnh vị và tổ hợp sách Kết nối tri thức ngắn gọn, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi trong SBT Toán 10 Bài 24 từ đó học tốt môn Toán 10.

SBT Toán 10 Kết nối tri thức Bài 24: Hoán vị, chỉnh hợp và tổ hợp

Bài 8.5 trang 55 SBT Toán 10 Tập 2: Có bao nhiêu cách xếp 6 lá thư khác nhau vào 6 chiếc phong bì khác nhau (mỗi lá thư vào trong một phong bì) ?

Lời giải:

Số cách xếp 6 lá thư khác nhau vào 6 chiếc phong bì khác nhau (mỗi lá thư vào trong một phong bì) chính là số các hoán vị của 6, nghĩa là bằng:

P₆ = 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720 (cách).

Bài 8.6 trang 55 SBT Toán 10 Tập 2: Có 12 thí sinh tham gia một cuộc thi âm nhạc. Hỏi có bao nhiêu cách trao ba giải cao nhất: Nhất, Nhì và Ba của cuộc thi cho các thí sinh ?

Lời giải:

Số cách trao giải bằng số cách lấy ra 3 người từ 12 thí sinh và xếp có thứ tự giữa họ, do đó, số cách trao ba giải cao nhất: Nhất, Nhì và Ba của cuộc thi là số các chỉnh hợp chập 3 của 12 phần tử và là:

$A_{12}^3=\frac{12!}{\left(12-3\right)!}=\frac{12.11.10.9!}{9!}=12.11.10=1320$(cách).

Bài 8.7 trang 55 SBT Toán 10 Tập 2: Minh có 4 vé xem bóng đá và muốn mời thêm các bạn đi xem cùng. Nhưng Minh có tới 6 người bạn thích bóng đá. Hỏi Minh có bao nhiêu cách mời 3 bạn để đi xem bóng đá cùng mình ?

Lời giải:

Minh có 4 vé xem bóng đá nên có thể mời thêm 3 bạn để đi xem cùng.

Mỗi cách chọn 3 bạn trong 6 bạn để đi xem bóng đá là một tổ hợp chập 3 của 6 phần tử.

Do đó, số cách chọn ra 3 người từ 6 người bạn là số các tổ hợp chập 3 của 6 phần tử và là:

$C_6^3=\frac{6!}{3!\left(6-3\right)!}=\frac{6.5.4.3!}{3!.3!}=\frac{6.5.4}{3.2.1}=20$ (cách).

Vậy Minh có tất cả 20 cách mời 3 bạn đi xem bóng đá cùng mình.

Bài 8.8 trang 55 SBT Toán 10 Tập 2: Ông An quyết định sơn ngôi nhà 4 tầng mới xây của mình bằng gam màu xanh. Hãng sơn mà ông An chọn có gam màu xanh với 10 màu xanh có mức độ đậm nhạt khác nhau.

a) Ông An có bao nhiêu cách sơn nhà sao cho 2 tầng khác nhau có màu khác nhau?

b) Sau khi tham khảo ý kiến của mọi người, ông điều chỉnh ý định ban đầu và bây giờ muốn các tầng sơn màu nhạt dần từ thấp lên cao. Số cách sơn nhà theo yêu cầu mới là bao nhiêu?

Lời giải:

a)

Để có một cách sơn, ông An cần chọn ra một bộ 4 màu sơn khác nhau, có sắp thứ tự (tương ứng với màu sơn của tầng 1, tầng 2, tầng 3 và tầng 4).

Do có 10 màu sơn nên số cách sơn là số các chỉnh hợp chập 4 của 10 và là:

$A_{10}^4=\frac{10!}{(10-4)!}=\frac{10.9.8.7.6!}{6!}=10.9.8.7=5040$ (cách).

b)

Để có một cách sơn nhà, ông An cần chọn ra 4 màu khác nhau từ 10 màu xanh rồi với mỗi bộ 4 màu đã chọn ra, ông An sắp thứ tự từ đậm nhất đến nhạt nhất để sơn các tầng từ thấp lên cao theo mong muốn.

Nói cách khác, với mỗi bộ 4 màu khác nhau, ông An có một cách sơn. Ngược lại, rõ ràng mỗi cách sơn phải dùng 4 màu khác nhau. Như vậy, số cách sơn bằng số cách chọn ra 4 màu sơn từ 10 màu sơn chính là số các tổ hợp chập 4 của 10 và là:

$C_{10}^4=\frac{10!}{4!(10-4)!}=\frac{10.9.8.7.6!}{4.3.2.1.6!}=\frac{10.9.8.7}{4.3.2.1}=210$ (cách).

Bài 8.9 trang 55 SBT Toán 10 Tập 2: Một nhóm hành khách, gồm 2 nam và 3 nữ, lên một chiếc xe buýt. Trên xe có 10 ghế trống, trong đó có 5 ghế cạnh cửa sổ.

a) Hỏi họ có bao nhiêu cách ngồi?

b) Các hành khách nữ mong muốn ngồi cạnh cửa sổ. Hỏi số cách ngồi của họ là bao nhiêu?

Lời giải:

a)

Số cách ngồi của nhóm hành khách chính là số cách chọn ra 5 chiếc ghế có xếp thứ tự từ 10 chiếc ghế trống, tương ứng với số các chỉnh hợp chập 5 của 10 và là:

$A_{10}^5=\frac{10!}{(10-5)!}=\frac{10.9.8.7.6.5!}{5!}=10.9.8.7.6=30240$ (cách).

b)

Việc xếp chỗ cho nhóm khách có thể được thực hiện theo 2 công đoạn:

– Công đoạn 1: xếp chỗ cho những hành khách nữ;

– Công đoạn 2: xếp chỗ cho những hành khách nam.

Với công đoạn 1, ta cần xếp chỗ cho 3 hành khách nữ vào 3 trong 5 chiếc ghế cạnh cửa sổ có xếp thứ tự. Số cách xếp là số các chỉnh hợp chập 3 của 5 và là:

$A_5^3=\frac{5!}{(5-3)!}=\frac{5.4.3.2!}{2!}=5.4.3=60$ (cách).

Đối với công đoạn 2, ta cần xếp chỗ cho 2 hành khách nam vào 2 trong bất kì 10 – 3 = 7 chiếc ghế còn lại (có xếp thứ tự). Số cách xếp là số các chỉnh hợp chập 2 của 7 và là:

$A_7^2=\frac{7!}{(7-2)!}=\frac{7.6.5!}{5!}=7.6=42$ (cách).

Như vậy, theo quy tắc nhân thì số cách xếp chỗ là:

60 . 42 = 2 520 (cách).

Bài 8.10 trang 55 SBT Toán 10 Tập 2: Để chuẩn bị cho buổi biểu diễn, 3 anh hề phải chọn trang phục biểu diễn cho mình gồm mũ, tóc giả, mũi và quần áo. Đoàn xiếc có 10 chiếc mũ, 6 bộ tóc giả, 5 cái mũi hề và 8 bộ quần áo hề. Hỏi các anh hề có bao nhiêu cách chọn trang phục biểu diễn ?

Lời giải:

Để chọn trang phục biểu diễn, các anh hề có thể thực hiện 4 công đoạn, gồm:

– Công đoạn 1: chọn mũ;

– Công đoạn 2: chọn tóc giả;

– Công đoạn 3: chọn mũi giả;

– Công đoạn 4: chọn quần áo.

Xét các công đoạn:

Công đoạn 1:

Có 3 anh hề và 10 chiếc mũ nên số cách chọn mũ để đội (có sắp xếp) cho 3 anh hề là số các chỉnh hợp chập 3 của 10 và là:

$A_{10}^3=\frac{10!}{(10-3)!}=\frac{10.9.8.7!}{7!}=10.9.8=720$ (cách).

Công đoạn 2:

Có 3 anh hề và 6 bộ tóc giả nên số cách chọn tóc giả (có sắp xếp) cho 3 anh hề là số các chỉnh hợp chập 3 của 6 và là:

$A_5^3=\frac{5!}{(5-3)!}=\frac{5.4.3.2!}{2!}=5.4.3=60$ (cách).

Công đoạn 3:

Có 3 anh hề và 5 mũi hề nên số cách chọn mũi hề (có sắp xếp) cho 3 anh hề là số các chỉnh hợp chập 3 của 5 và là:

$A_5^3=\frac{5!}{(5-3)!}=\frac{5.4.3.2!}{2!}=5.4.3=60\left(cách\right).$

Công đoạn 4:

Có 3 anh hề và 8 bộ quần áo nên số cách chọn quần áo (có sắp xếp) cho 3 anh hề là số các chỉnh hợp chập 3 của 8 và là:

$A_8^3=\frac{8!}{(8-3)!}=\frac{8.7.6.5!}{5!}=8.7.6=336$ (cách)

Như vậy, theo quy tắc nhân thì số cách chọn trang phục của 3 anh hề là:

720 . 120 . 60 . 336 = 1 741 824 000 (cách).

Bài 8.11 trang 55 SBT Toán 10 Tập 2: Trong các số tự nhiên từ 1 đến 999 999, có bao nhiêu số chứa đúng một chữ số 1 và đúng một chữ số 2.

Lời giải:

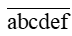
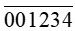
Các số từ 1 đến 999 999 có thể được viết một cách duy nhất dưới dạng , trong đó mỗi kí hiệu a, b, c, d, e, f nhận một trong các giá trị 0; 1; 2;..., 9. Chẳng hạn số  được hiểu là số 1234.

Để tạo thành một số 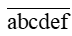 thoả mãn yêu cầu chứa đúng một chữ số 1 và đúng một chữ số 2, ta có thể tiến hành qua hai công đoạn:

– Công đoạn 1: chọn ra 2 kí hiệu trong số a, b, c, d, e, f để thay bằng các chữ số 1; 2;

– Công đoạn 2: thay 4 kí hiệu còn lại, mỗi kí hiệu bằng một chữ số bất kì trong số tám chữ số còn lại 0; 3; 4;...; 9.

Xét công đoạn 1: Chọn ra 2 kí hiệu từ 6 kí hiệu để thay chúng tương ứng bằng 1; 2 (có sắp xếp), số cách chọn là số các chỉnh hợp chập 2 của 6 và là:

$A_6^2=\frac{6!}{(6-2)!}=\frac{6.5.4!}{4!}=6.5=30$ (cách)

Xét công đoạn 2: Thay 4 kí hiệu còn lại, mỗi kí hiệu bằng một chữ số bất kì trong số tám chữ số còn lại 0; 3; 4;...; 9. Tức là mỗi kí hiệu còn lại có thể được thay bằng 8 cách khác nhau. Do đó có tổng cộng: 8 . 8 . 8 . 8 = 4 096 (cách).

Vậy, theo quy tắc nhân, số các số từ 1 đến 999 999 cần tìm là:

30 . 4 096 = 122 880 (số).

Bài 8.12 trang 55 SBT Toán 10 Tập 2: Trong các số tự nhiên từ 1 đến 999 999, có bao nhiêu số chứa đúng một chữ số 1 và đúng một chữ số 2.

a) Có bao nhiêu cách sắp xếp các chữ cái của từ “KHIÊNG” thành một dãy kí tự gồm 6 chữ cái khác nhau (có thể là vô nghĩa) ?

b) Cùng câu hỏi như a) nhưng yêu cầu hai chữ cái đầu tiên là các phụ âm ?

c) Giống câu hỏi a) nhưng yêu cầu các phụ âm phải đứng liên tiếp với nhau.

Lời giải:

a)

Từ “KHIÊNG” có 6 chữ cái khác nhau. Do đó, số cách sắp xếp 6 chữ cái khác nhau vào 6 vị trí theo yêu cầu là:

6! = 6 . 5 . 4 . 3 . 2 . 1 = 720 (cách).

b)

Từ “KHIÊNG” có 4 phụ âm là K, H, N và G. Việc sắp xếp 6 chữ cái thoả mãn yêu cầu hai chữ cái đầu tiên là các phụ âm có thể được thực hiện qua hai công đoạn:

– Công đoạn 1: chọn 2 trong số 4 phụ âm để xếp vào hai vị trí đầu tiên;

– Công đoạn 2: xếp 6 – 2 = 4 chữ cái còn lại vào 4 vị trí tiếp theo.

Xét công đoạn 1:

Số các cách chọn ra 2 trong 4 phụ âm để xếp vào hai vị trí đầu tiên là:

$A_4^2=\frac{4!}{(4-2)!}=\frac{4.3.2!}{2!}=4.3=12$ (cách).

Xét công đoạn 2: Xếp 6 – 2 = 4 chữ cái còn lại vào 4 vị trí tiếp theo.

Số các cách xếp 4 chữ cái còn lại vào 4 vị trí tiếp theo là: 4! = 4 . 3 . 2 . 1 = 24 (cách).

Theo quy tắc nhân, số cách sắp xếp cần tìm là:

12 . 24 = 288 (cách).

c)

Có 4 phụ âm trong từ “KHIÊNG” và ta yêu cầu chúng phải đứng liên tiếp nhau, do đó có ba phương án cho vị trí của các phụ âm:

– Phương án 1: vị trí các phụ âm (từ trái qua phải) là 1, 2, 3, 4;

– Phương án 2: vị trí các phụ âm (từ trái qua phải) là 2, 3, 4, 5;

– Phương án 3: vị trí các phụ âm (từ trái qua phải) là 3, 4, 5, 6.

+) Đối với phương án 1, việc xếp các chữ cái được thực hiện qua hai công đoạn:

– Công đoạn 1: xếp 4 phụ âm vào các vị trí 1, 2, 3, 4;

– Công đoạn 2: xếp 2 nguyên âm vào 2 vị trí còn lại.

Số các cách xếp 4 phụ âm vào 4 vị trí là:

4! = 4 . 3 . 2 . 1 = 24 (cách).

Số các cách xếp 2 nguyên âm vào 2 vị trí còn lại là:

2! = 2 . 1 = 2 (cách).

Vậy, theo quy tắc nhân thì số cách xếp theo phương án 1 là:

24 . 2 = 48 (cách).

+) Đối với phương án 2, việc xếp các chữ cái được thực hiện qua hai công đoạn:

– Công đoạn 1: xếp 4 phụ âm vào các vị trí 2, 3, 4, 5;

– Công đoạn 2: xếp 2 nguyên âm vào 2 vị trí còn lại.

Số các cách xếp 4 phụ âm vào 4 vị trí là:

4! = 4 . 3 . 2 . 1 = 24 (cách).

Số các cách xếp 2 nguyên âm vào 2 vị trí còn lại là:

2! = 2 . 1 = 2 (cách).

Vậy, theo quy tắc nhân thì số cách xếp theo phương án 2 là:

24 . 2 = 48 (cách).

+) Đối với phương án 3, việc xếp các chữ cái được thực hiện qua hai công đoạn:

– Công đoạn 1: xếp 4 phụ âm vào các vị trí 3, 4, 5, 6;

– Công đoạn 2: xếp 2 nguyên âm vào 2 vị trí còn lại.

Số các cách xếp 4 phụ âm vào 4 vị trí là:

4! = 4 . 3 . 2 . 1 = 24 (cách).

Số các cách xếp 2 nguyên âm vào 2 vị trí còn lại là:

2! = 2 . 1 = 2 (cách).

Vậy, theo quy tắc nhân thì số cách xếp theo phương án 3 là:

24 . 2 = 48 (cách).

Vì thế, theo quy tắc cộng thì số cách xếp thoả mãn là:

48 + 48 + 48 = 144 (cách).