Với giải Câu hỏi trang 25 Toán 10 Tập 1 Kết nối tri thức trong Bài 3: Bất phương trình bậc nhất hai ẩn học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Kết nối tri thức trang 25 Bài 3: Bất phương trình bậc nhất hai ẩn

Vận dụng trang 25 SGK Toán lớp 10 Tập 1: Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Em có thể sử dụng bao nhiêu phút gọi nội mạng và bao nhiêu phút gọi ngoại mạng trong một tháng nếu em muốn số tiền phải trả ít hơn 200 nghìn đồng?

Phương pháp giải:

Bước 1: Gọi x là số phút gọi nội mạng ($x\in \mathbb{N}$), y là số phút gọi ngoại mạng ($y\in \mathbb{N}$) và biến đổi bài toán đã cho thành bài toán tìm miền nghiệm của bất phương trình.

Bước 2: Xác định miền nghiệm.

Lời giải:

Bước 1:

Gọi x là số phút gọi nội mạng ($x\in \mathbb{N}$), y là số phút gọi ngoại mạng ($y\in \mathbb{N}$)

Số tiền cần phải trả là $x+2y$ nghìn đồng.

Để số tiền phải trả ít hơn 200 nghìn đồng thì $x+2y<200$.

Như vậy, bài toán trở thành tìm miền nghiệm của bất phương trình $x+2y<200$

Bước 2:

Xác định miền nghiệm:

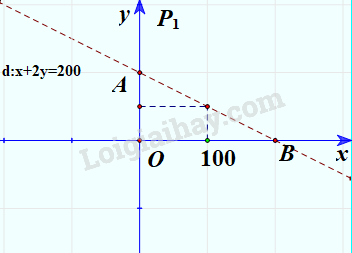
+ Vẽ đường thẳng d: x+2y=200 (nét đứt).

+ Thay tọa độ O(0;0) vào biểu thức x+2y ta được 0+2.0=0<200

=> Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d.

Vậy nếu số phút sử dụng nội mạng là x và ngoại mạng là y mà điểm (x;y) nằm trong miền tam giác OAB không kể đoạn AB thì số tiền phải trả thấp hơn 200 nghìn đồng.

Chú ý

x và y là số tự nhiên nên cần lấy phần không âm của trục Ox và phần không âm của trục Oy.

Bài tập

Bài 2.1 trang 25 SGK Toán lớp 10 Tập 1: Bất phương trình nào sau đây là bất phương tình bậc nhất hai ẩn?

a) 2x+3y > 6

b) $2^{2}x+y\le 0$

c) $2x^2-y\ge 1$

Lời giải:

a) Ta có hệ số a=2, b=3, c=6 và các ẩn là x và y.

=> bất phương trình 2x+3y>6 là bất phương trình bậc nhất hai ẩn.

b) Ta có $2^{2}x+y\le 0\iff 4x+y\le 0$

=> a=4,b=1 và c=0. Các ẩn là x và y

=> $2^{2}x+y\le 0$ là bất phương trình bậc nhất hai ẩn.

c) $2x^2-y\ge 1$ có bậc của x là 2 nên đây không là bất phương trình bậc nhất hai ẩn.

Chú ý

Khi bậc của x và y lớn hơn 1 thì bất phương trình bài cho không là bất phương trình bậc nhất hai ẩn.

Bài 2.2 trang 25 SGK Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:

a) $3x+2y\ge 300$

b) $7x+20y<0$

Lời giải:

a)

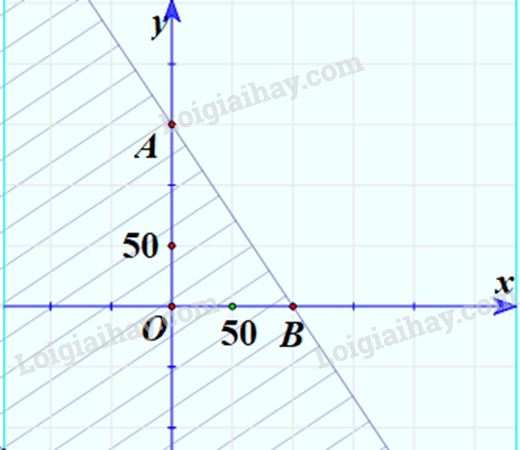
Bước 1: Vẽ đường thẳng $3x+2y=300$

Bước 2: Thay tọa độ điểm O(0;0) vào 3x+2y ta được 3.0+2.0<300

=> Điểm O không thuộc miền nghiệm.

=> Miền nghiệm của bất phương trình là nửa mặt phẳng có bờ 3x+2y=300 và không chứa điểm O.

b)

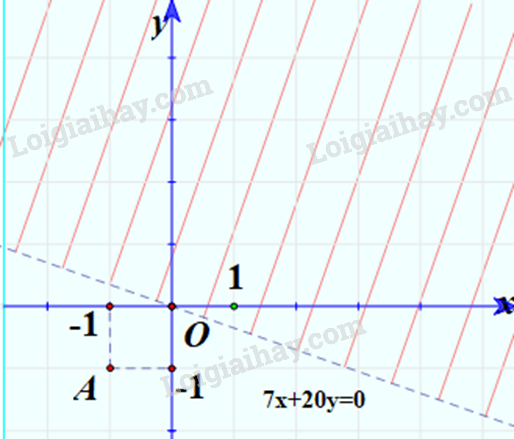
Bước 1: Vẽ đường thẳng 7x+20y=0 (nét đứt)

Bước 2: Vì c=0 nên ta thay tọa độ điểm A(-1;-1) vào biểu thức 7x+20y ta được:

7.(-1)+20.(-1)=-27<0

=> Điểm A thuộc miền nghiệm

=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng 7x+20y=0 và không chứa điểm A (không kể đường thẳng 7x+20y=0)

Bài 2.3 trang 25 SGK Toán lớp 10 Tập 1: Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và

trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho

tổng số tiền ông An phải trả không quá 14 triệu đồng.

b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ.

Lời giải:

a)

Ta có 14 triệu = 14 000 (nghìn đồng)

Số tiền ông An đi x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)

Số tiền ông An đi y km trong 2 cuối tuần là 10y (nghìn đồng)

Số tiền ông An đi trong một tuần là 8x+10y (nghìn đồng)

Vì số tiền không quá 14 triệu đồng nên ta có :

$\begin{array}{l}8x+10y\le 14000\\ \iff 4x+5y\le 7000\end{array}$

Vậy bất phương trình cần tìm là $4x+5y\le 7000$

b)

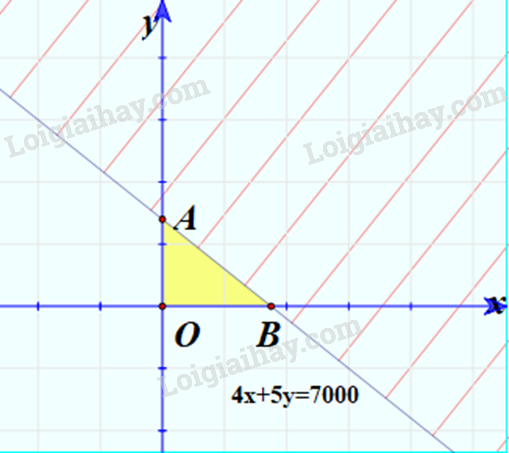
Bước 1: Vẽ đường thẳng $4x+5y=7000$(nét liền)

Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:

4.0+5.0=0<7000

=> Điểm O thuộc miền nghiệm

=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng $4x+5y=7000$ và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

Chú ý

Khi bài cho số ki lô mét thì ta cần tính theo quãng đường di chuyển.