Với giải Câu hỏi trang 89 Toán 10 Tập 2 Kết nối tri thức trong Bài tập cuối chương 9 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Kết nối tri thức trang 89: Bài tập cuối chương 9

Bài 9.20 trang 89 SGK Toán 10 Tập 2: Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất của các biến cố:

F: “Trong ba ngày, có đúng một ngày có mưa”;

G: “Trong ba ngày, có ít nhất hai ngày không mưa”.

Lời giải:

a) Ta kí hiệu mưa là M và không mưa là KM.

Theo bài ra ta vẽ được sơ đồ hình cây mô tả không gian mẫu như sau: 

Do đó, Ω = {M – M – M; M – M – KM; M – KM – M; M – KM – KM; KM – M – M; KM – M – KM; KM – KM – M; KM – KM – KM}.  

Vậy n(Ω) = 8.

b)

+ Biến cố F: “Trong ba ngày, có đúng một ngày có mưa”;

Theo sơ đồ ở câu a, ta có: F = {M – KM – KM; KM – M – KM; KM – KM – M}.

Do đó, n(F) = 3. 

Vậy $P\left(F\right)=\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{3}{8}.$

+ Biến cố G: “Trong ba ngày, có ít nhất hai ngày không mưa”. (có 2 trường hợp, một là 2 ngày không mưa và hai là cả 3 ngày không mưa).

Theo sơ đồ ở câu a, ta có G = {M – KM – KM; KM – M – KM; KM – KM – M; KM – KM – KM}.

Do đó, n(G) = 4. 

Vậy $P\left(G\right)=\frac{n\left(G\right)}{n\left(\Omega \right)}=\frac{4}{8}=\frac{1}{2}.$

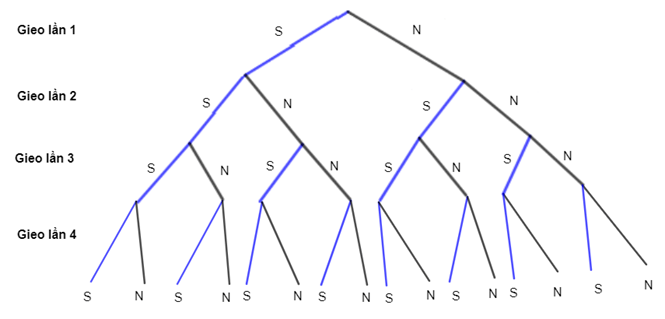
Bài 9.21 trang 89 SGK Toán 10 Tập 2: Gieo một đồng xu cân đối liên tiếp bốn lần.

a) Vẽ sơ đồ hình cây mô tả không gian mẫu.

b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.

Lời giải:

a) Đồng xu cân đối nên các kết quả có thể là đồng khả năng.

Kí hiệu S và N tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa.

Theo bài ra ta có sơ đồ hình cây mô tả không gian mẫu như sau: 

Do đó, n(Ω) = 16.

b) Gọi biến cố A: “Trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”.

Theo sơ đồ hình cây ở câu a, ta có: 

A = {SSNN; SNSN; SNNS; NSSN; NSNS; NNSS}.

Do đó, n(A) = 6. 

Vậy $P\left(G\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{16}=\frac{3}{8}.$

Bài 9.22 trang 89 SGK Toán 10 Tập 2: Chọn ngẫu nhiên 4 viên bi từ một túi đựng 4 viên bi đỏ và 6 viên bi xanh đôi một khác nhau. Gọi A là biến cố: “Trong bốn viên bi đó có cả bi đỏ và cả bi xanh”. Tính P(A) và P($\overline{A}$).

Lời giải:

Phép thử là chọn ngẫu nhiên 4 viên bi từ túi gồm 10 viên bi (4 viên bi đỏ và 6 viên bi xanh). 

Chọn 4 viên bi từ 10 viên bi, thì số cách chọn là: $C_{10}^4$= 210 (cách).

Do đó, số phần tử của không gian mẫu là n(Ω) = 210. 

Xét biến cố A, để có cả bi đỏ và bi xanh thì ta có các trường hợp sau:

+ Trường hợp 1: chọn 1 bi xanh trong 6 bi xanh, 3 bi đỏ trong 4 bi đỏ, số cách chọn là: $C_6^1.C_4^3=$24. 

+ Trường hợp 2: chọn 2 bi xanh trong 6 bi xanh, 2 bi đỏ trong 4 bi đỏ, số cách chọn là: $C_6^2.C_4^2$= 90.

+ Trường hợp 3: chọn 3 bi xanh trong 6 bi xanh, 1 bi đỏ trong 4 bi đỏ, số cách chọn là: $C_6^3.C_4^1$= 80.

Do các trường hợp là rời nhau nên n(A) = 24 + 90 + 80 = 194.

Vậy $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{194}{210}=\frac{97}{105}.$

Từ đó suy ra, P($\overline{A}$) = 1 –  P(A) = $1-\frac{97}{105}=\frac{8}{105}$.