Với giải Câu hỏi trang 26 Toán 10 Tập 2 Cánh Diều trong Bài 5: Số gần đúng sai số học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Cánh Diều trang 26 Bài 1: Số gần đúng. Sai số
Hoạt động 7 trang 26 Toán lớp 10 Tập 2: Như đã biết, nếu số đúng là số nguyên hoặc số thập phân thì ta có thể tìm dễ dàng số gần đúng với độ chính xác cho trước bằng cách quy tròn về hàng thích hợp. Tuy nhiên, việc biểu diễn số thực về dạng số nguyên hoặc số thập phân trong thực tiễn là không đơn giản. Ngày nay, ta có thể sử dụng máy tính cầm tay hoặc các phương tiện tính toán hiện đại để giải quyết vấn đề đó.
Sử dụng máy tính cầm tay, tính 37.√14 (trong kết quả lấy bốn chữ số ở phần thập phân).
Lời giải:
Để thực hiện phép tính trên ra kết quả có bốn chữ số ở phần thập phân, ta có thể làm như sau:

Luyện tập 2 trang 26 Toán lớp 10 Tập 2: Sử dụng máy tính cầm tay, tính 3√15:5-2 (trong kết quả lấy hai chữ số ở phần thập phân)
Nội dung bài viết
Lời giải:
Để thực hiện phép tính trên ra kết quả có hai chữ số ở phần thập phân, ta có thể làm như sau:

Lời giải:
Theo https://vi.wikipedia.org:
+ Khối lượng của Trái Đất khoảng 5,9722 × 1024 (kg).
+ Khối lượng của Mặt Trời là (1,98855 ± 0,00025) × 1030 kg.
Bài tập
Bài 1 trang 26 Toán lớp 10 Tập 2: Quy tròn số – 3,2475 đến hàng phần trăm. Số gần đúng nhận được có độ chính xác là bao nhiêu?
Lời giải:
Quy tròn số – 3,2475 đến hàng phần trăm ta được – 3,25.
Sai số tuyệt đối là ∆ = |– 3,2475 – (– 3,25)| = 0,0025 < 0,005.
Vậy số gần đúng – 3,25 có độ chính xác là d = 0,005.
(Ta có thể tìm độ chính xác bằng cách lấy nửa đơn vị của hàng quy tròn).
Bài 2 trang 26 Toán lớp 10 Tập 2: Viết số quy tròn của mỗi số gần đúng sau với độ chính xác d:
a, 30,2376 với d = 0,009
b, 2,3512082 với d = 0,008
Bài 3 trang 26 Toán lớp 10 Tập 2: Ta đã biết 1 inch (kí hiệu là in) là 2,54 cm. Màn hình của một chiếc ti vi có dạng hình chữ nhật với độ dài đường chéo là 32 in, tỉ số giữa chiều dài và chiều rộng của màn hình là 16 : 9. Tìm một giá trị gần đúng (theo đơn vị inch) của chiều dài màn hình ti vi và tìm sai số tương đối, độ chính xác của số gần đúng đó.
Lời giải:
Ta mô phỏng màn hình ti vi có hình chữ nhật ABCD như sau:
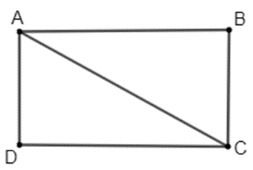
Ta có: AC = 32 in, AB là chiều dài, BC là chiều rộng với AB : BC = 16 : 9.
Gọi chiều dài của ti vi là x (in, x > 0) hay AB = x, khi đó chiều rộng của ti vi là BC=916x
Sử dụng định lí Pythagore, ta có phương trình: x2+(916x)2=322 (*).
Giải phương trình (*), ta có:
(*) ⇔x2+81256x2=1024⇔337256x2=1024⇔x2=262144337
Do x > 0 nên x = 512√337.
Vậy chiều dài của chiếc ti vi là 512√337=27,89041719... (in).
Quy tròn số 512√337 đến hàng phần trăm được 27,89.
Ta có độ chính xác d = 0,005 (nửa đơn vị hàng quy tròn).
Vậy sai số tương đối δa≤0,00527,89≈0,02%.
Xem thêm các lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:
Hoạt động 2 trang 22 Toán lớp 10 Tập 2: Một bồn hoa có dạng hình tròn với bán kính là 0,8 m...
Hoạt động 3 trang 23 Toán lớp 10 Tập 2: Hãy ước lượng sai số tuyệt đối ∆S1 ở Ví dụ 1...
Luyện tập 1 trang 25 Toán lớp 10 Tập 2: Hãy viết số quy tròn của số gần đúng a = 28,4156 biết ![]() ...
...
Luyện tập 2 trang 26 Toán lớp 10 Tập 2: Sử dụng máy tính cầm tay, tính....
Bài 1 trang 26 Toán lớp 10 Tập 2: Quy tròn số – 3,2475 đến hàng phần trăm. Số gần đúng nhận...
Bài 2 trang 26 Toán lớp 10 Tập 2: Viết số quy tròn của mỗi số gần đúng sau với độ chính xác d...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.