Với Giải SBT Toán 10 Tập 2 trong Bài 4: Nhị thức Newton Sách bài tập Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

SBT Toán 10 Cánh diều Bài 4: Nhị thức Newton

Bài 28 trang 15 SBT Toán 10: Trong các phát biểu sau, phát biểu nào sai?

A. (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.

B. (a – b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴.

C. (a + b)⁴ = b⁴ + 4b³a + 6b²a² + 4ba³ + a⁴.

D. (a + b)⁴ = a⁴ + b⁴.

Lời giải:

Đáp án đúng là D

Công thức khai triển nhị thức Newton (a + b)⁴ là:

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ = b⁴ + 4b³a + 6b²a² + 4ba³ + a⁴.

Do đó phương án A, C đúng, phương án D sai.

Công thức khai triển nhị thức Newton (a – b)⁴ là:

(a + b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴.

Do đó phương án B đúng.

Vậy ta chọn phương án D.

Câu hỏi trang 16 SBT Toán 10

Bài 29 trang 16 SBT Toán 10: Trong các phát biểu sau, phát biểu nào đúng?

A. (a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

B. (a – b)⁵ = a⁵ – 5a⁴b + 10a³b² + 10a²b³ – 5ab⁴ + b⁵.

C. (a + b)⁵ = a⁵ + b⁵.

D. (a – b)⁵ = a⁵ – b⁵.

Lời giải:

Công thức khai triển nhị thức Newton (a + b)⁵ là:

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵.

Do đó phương án A đúng, phương án C sai.

Công thức khai triển nhị thức Newton (a – b)⁵ là:

(a – b)⁵ = a⁵ – 5a⁴b + 10a³b² – 10a²b³ + 5ab⁴ – b⁵.

Do đó các phương án B, D sai.

Vậy ta chọn phương án A.

Bài 30 trang 16 SBT Toán 10: Hệ số của x³ trong khai triển biểu thức (2x – 1)⁴ là:

A. 32.

B. –32.

C. 8.

D. –8.

Lời giải:

Đáp án đúng là B

Ta có: (2x – 1)⁴ = (2x)⁴ – 4.(2x)³.1 + 6.(2x)².1² – 4.(2x).1³ + 1⁴

= 16x⁴ – 32x³ + 24x² – 8x + 1

Số hạng chứa x³ trong khai triển biểu thức (2x – 1)⁴ là –32x³.

Vậy hệ số của x³ trong khai triển biểu thức (2x – 1)⁴ là –32.

Do đó ta chọn phương án B.

Bài 31 trang 16 SBT Toán 10: Hệ số của x trong khai triển biểu thức (x – 2)⁵ là:

A. 32.

B. –32.

C. 80.

D. –80.

Lời giải:

Đáp án đúng là C

Ta có: (x – 2)⁵ = x⁵ – 5x⁴.2 + 10x³.2² – 10x².2³ + 5x.2⁴ – 2⁵

= x⁵ – 10x⁴ + 40x³ – 80x² + 80x – 32

Số hạng chứa x trong khai triển biểu thức (x – 2)⁵ là 80x.

Vậy hệ số của x trong khai triển biểu thức (x – 2)⁵ là 80.

Do đó ta chọn phương án C.

Bài 32 trang 16 SBT Toán 10: Khai triển các biểu thức sau:

a) (4x + 1)⁴;

b) (5x – 3)⁴;

c) ${\left(\frac{1}{3}x+5\right)}^5$;

d) ${\left(3x-\frac{1}{3}\right)}^5$.

Lời giải:

a) (4x + 1)⁴ = (4x)⁴ + 4.(4x)³.1 + 6.(4x)².1² + 4.4x.1³ + 1⁴

= 256x⁴ + 256x³ + 96x² + 16x + 1.

b) (5x – 3)⁴ = (5x)⁴ + 4.(5x)³.(–3) + 6.(5x)².(–3)² + 4.5x.(–3)³ + (–3)⁴

= 625x⁴ – 1500x³ + 1350x² – 540x + 81.

c) 

.

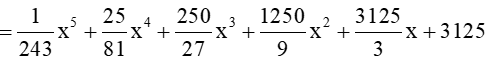
d) 

Bài 33 trang 16 SBT Toán 10: Xác định hệ số của x² trong khai triển biểu thức (4x – 3)⁴.

Lời giải:

Ta có: (4x – 3)⁴ = (4x)⁴ – 4.(4x)³.3 + 6.(4x)².3² – 4.4x.3³ + 3⁴

= 256x⁴ – 768x³ + 864x² – 432x + 81

Số hạng chứa x² trong khai triển biểu thức (4x – 3)⁴ là 864x².

Vậy hệ số của x² trong khai triển biểu thức (4x – 3)⁴ là 864.

Bài 34 trang 16 SBT Toán 10: Xác định hệ số của x³ trong khai triển biểu thức ${\left(\frac{2}{3}x+\frac{1}{4}\right)}^5$.

Lời giải:

Tacó: 

Số hạng chứa x³ trong khai triển biểu thức ${\left(\frac{2}{3}x+\frac{1}{4}\right)}^5$ là $\frac{5}{27}{x}^3$.

Vậy hệ số của x³ trong khai triển biểu thức ${\left(\frac{2}{3}x+\frac{1}{4}\right)}^5$ là $\frac{5}{27}$.

Bài 35 trang 16 SBT Toán 10: Cho 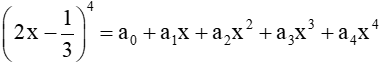. Tính:

a) a₂;

b) a₀ + a₁ + a₂ + a₃ + a₄.

Lời giải:

a) Ta có:

Ta thấy a₂ là hệ số của x².

Số hạng chứa x² trong khai triển biểu thức ${\left(2x-\frac{1}{3}\right)}^4$ là $\frac{8}{3}{x}^2$.

Suy ra hệ số của x² trong khai triển biểu thức ${\left(2x-\frac{1}{3}\right)}^4$ là $\frac{8}{3}$.

Tức là, $a_2=\frac{8}{3}$.

b) Ta có 

Chọn x = 1, ta được:

${\left(2.1-\frac{1}{3}\right)}^4$= a₀ + a₁ + a₂ + a₃ + a₄ = a₀ + a₁.1 + a₂.1² + a₃.1³ + a₄.1⁴

⇔$\frac{625}{81}$ = a₀ + a₁ + a₂ + a₃ + a₄.

Vậy a₀ + a₁ + a₂ + a₃ + a₄ = $\frac{625}{81}$.

Bài 36 trang 16 SBT Toán 10: Cho ${\left(\frac{3}{5}x+\frac{1}{2}\right)}^5$= a₀ + a₁.x + a₂.x² + a₃.x³ + a₄.x⁴ + a₅.x⁵_. Tính:

a) a₃;

b) a₀ + a₁ + a₂ + a₃ + a₄ + a₅.

Lời giải:

Tacó: 

Ta thấy a₃ là hệ số của x³.

Số hạng chứa x³ trong khai triển biểu thức ${\left(\frac{3}{5}x+\frac{1}{2}\right)}^5$ là $\frac{27}{50}{x}^3$.

Suy ra hệ số của x³ trong khai triển biểu thức ${\left(\frac{3}{5}x+\frac{1}{2}\right)}^5$ là $\frac{27}{50}$.

Tức là, a₃=$\frac{27}{50}$.

b) Ta có a₀ + a₁ + a₂ + a₃ + a₄ + a₅ = a₀ + a₁.1 + a₂.1² + a₃.1³ + a₄.1⁴ + a₅.1⁵

$={\left(\frac{3}{5}.1+\frac{1}{2}\right)}^5=\frac{161051}{100000}$.

Vậy a₀ + a₁ + a₂ + a₃ + a₄ + a₅ = $\frac{161051}{100000}$.

Bài 37 trang 16 SBT Toán 10: Tính các tổng sau (không sử dụng máy tính cầm tay):

a) T = $C_4^0+\frac{1}{2}{C}_4^1+\frac{1}{3}{C}_4^2+\frac{1}{4}{C}_4^3+\frac{1}{5}{C}_4^4$;

b) S = $C_6^1+2C_6^2+3C_6^3+4C_6^4+5C_6^5+6C_6^6$.

Lời giải:

a) Áp dụng kết quả $\frac{1}{k+1}{C}_n^k=\frac{1}{n+1}{C}_{n+1}^{k+1}$ với 0 ≤ k ≤ n (chứng minh ở Bài 27a trang 14 SBT Toán 10 Tập 2), ta được:

Vậy T=$\frac{31}{5}$.

b) Áp dụng kết quả $k{C}_n^k=n{C}_{n-1}^{k-1}$ với 1 ≤ k ≤ n (chứng minh ở Bài 27b trang 14 SBT Toán 10 Tập 2), ta được:

= 6.(1 + 1)⁵ = 6.2⁵ = 192.

Vậy S = 192.