Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 114, 115, 116 Bài 2: Hình hộp chữ nhật (tiếp) chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 114, 115, 116 Toán 8 Bài 2: Hình hộp chữ nhật (tiếp)

Câu hỏi Vở bài tập 8 trang 114 - 116: Đúng ghi Đ, sai ghi S vào ô trống trong mỗi khẳng định ở các câu sau đây.

Phương pháp giải: Sử dụng lý thuyết đã được nêu trong sách giáo khoa để nhận xét tính đúng sai của từng đáp án.
Lời giải:

Câu 4: Sai vì chúng có thể không cùng nằm trong bất kì mặt phẳng nào.

Câu 5: Đúng.

Câu 6: Sai vì chúng có thể không cùng nằm trong bất kì mặt phẳng nào, không nhất thiết phải song song.

Câu 7:

a) Đúng.

b) Sai vì có thể xảy ra trường hợp hai đường thẳng đó cắt nhau và cùng nằm trong mặt phẳng song song với mặt phẳng đã cho.

Ta điền vào bảng như sau:

Vở bài tập Toán 8 trang 114 - 116 Bài 5: $ABCD.A{}_1{B}_1{C}_1{D}_1$  là một hình lập phương (h.66). Quan sát hình và cho biết:

a) Những cạnh nào song song với cạnh $C_{1}C$?

b) Những cạnh nào song song với cạnh  $A_1{D}_1$?

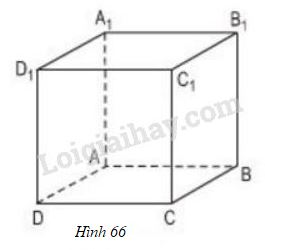
Phương pháp giải: Áp dụng tính chất của hình lập phương.
Lời giải:

Vì sáu mặt của hình lập phương là hình vuông, do đó ta có:

a) Trong mặt phẳng $(B_{1}BC{C}_1)$:$C_{1}C//B_{1}B$  (1)

Trong mặt phẳng $(C_{1}CD{D}_1)$:$C_{1}C//D_{1}D$  (2)

Trong mặt phẳng $(A_{1}AB{B}_1)$:$A_{1}A//B_{1}B$  (3)

Từ (1) và (3), $C_{1}C$ và $A_{1}A$ cùng song song với $B_{1}B$ do đó $C_{1}C//A_{1}A$ (4)

Vậy $A_{1}A,B_{1}B,D_{1}D$ cùng song song với $C_{1}C$.

b) Trong mặt phẳng $(A_1{B}_1{C}_1{D}_1)$: $A_1{D}_1//B_1{C}_1$ (5)

Trong mặt phẳng $(A_{1}AD{D}_1)$: $A_1{D}_1//AD$ (6)

Trong mặt phẳng $(ABCD)$: $BC//AD$ (7)

Từ (6) và (7), $A_1{D}_1$ và $BC$ cùng song song với $AD$, do đó $A_1{D}_1//BC$.

Vậy $B_1{C}_1,AD$ và $BC$ cùng song song với $A_1{D}_1$.

Vở bài tập Toán 8 trang 114 - 116 Bài 6: Một căn phòng dài $4,5m$, rộng $3,7m$ và cao $3,0m$. Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là $5,8m^2$. Hãy tính diện tích cần quét vôi.

Phương pháp giải:

Diện tích cần quét vôi = diện tích bốn bức tường + diện tích trần - diện tích cửa.

Hay: Diện tích cần quét vôi = diện tích xung quanh + diện tích trần - diện tích cửa.

Tính diện tích xung quanh theo công thức $S_{xq}=(a+b)\times 2\times c$, với $a$ là chiều dài, $b$ là chiều rộng, $c$ là chiều cao

Lời giải: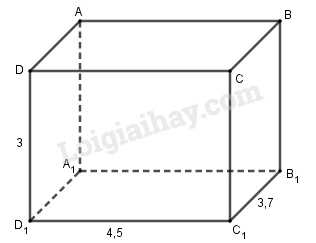

Giả sử căn phòng là hình hộp chữ nhật có kích thước như hình 67. Ta phải quét vôi trần nhà $ABCD$ và bốn bức tường xung quanh. Vì sáu mặt của hình hộp chữ nhật đều là hình chữ nhật, do dó ta có:

Diện tích trần nhà là:

$S_{ABCD}=S_{A_1{B}_1{C}_1{D}_1}$ $=4,5\times 3,7$ $=16,65(m^2)$

Diện tích bốn bức tường xung quanh là:

$S_{xq}=(2.(B_1{C}_1+C_1{D}_1)).D{D}_1$ $=2.(3,7+4,5).3=49,2(m^2)$

Diện tích cần quét vôi là:

$16,65+49,2-5,8=60,05(m^2)$

Vở bài tập Toán 8 trang 114 - 116 Bài 7: Hình 68 vẽ một phòng ở. Quan sát hình và giải thích vì sao:

a) Đường thẳng $b$ song song với mp $(P)$?

b) Đường thẳng $p$ song song với sàn nhà?

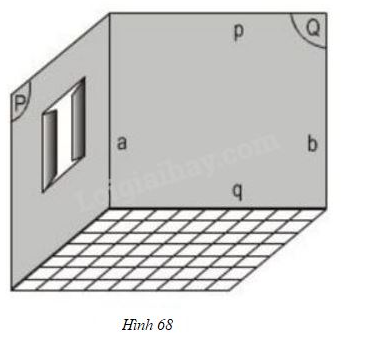
Phương pháp giải: Sử dụng kết quả: "Đường thẳng  không nằm trong mặt phẳng  mà song song với đường thẳng  nằm trong mặt phẳng  thì đường thẳng  song song với mặt phẳng " để giải thích các câu hỏi a) và b) của bài toán.
Lời giải:

a) Ta có $a\subset mp(P);a//b$ .

Mặt khác $b$ không thuộc mp$(P)$

Do đó, $b//mp(P)$ .

b) Ta có $p$  không thuộc sàn nhà và đường thẳng $p$ song song với đường thẳng $q$  trong sàn nhà nên $p$ song song với sàn nhà.

a) Hãy kể tên các cạnh khác song song với mặt phẳng $(EFGH)$

b) Cạnh $CD$ song song với những mặt phẳng nào của hình hộp chữ nhật?

c) Đường thẳng $AH$ không song song với mặt phẳng $(EFGH)$, hãy chỉ ra mặt phẳng song song với đường thẳng đó.

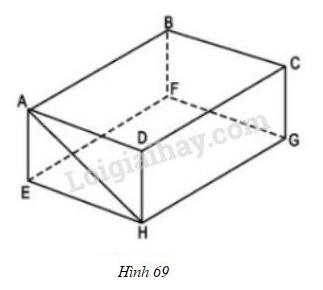
Phương pháp giải:

Áp dụng các định nghĩa:

- Hình hộp chữ nhật.

- Khi đường thẳng $d$ không nằm trong mặt phẳng $(ABCD)$ mà $d$ song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng $d$ song song với mặt phẳng $(ABCD)$.

- Hình bình hành.

Lời giải:

a) Ta biết, $6$ mặt của hình hộp chữ nhật đều là hình chữ nhật, do đó ta có:

$BC//FG$ mà $FG\subset mp\left(EFGH\right)$, suy ra $BC//mp(EFGH)$

$AD//EH$ mà $EH\subset mp\left(EFGH\right)$, suy ra $AD//mp(EFGH)$

$DC//HG$ mà $HG\subset mp\left(EFGH\right)$, suy ra $DC//mp(EFGH)$

b) $CD//AB$ mà $AB\subset mp\left(ABFE\right)$, suy ra $CD//mp(ABFE)$

$CD//mp(EFGH)$ đã nói ở câu a)

Vậy $CD$ song song với hai mặt phẳng $(ABFE)$ và $(EFGH)$.

c) Kẻ thêm đường chéo $BG$ của hình chữ nhật $BCGF$.

Xét tứ giác $ABGH$, ta có:

$AB=GH$ (vì cùng bằng $CD$)  (1)

$AH=BG$ (vì là đường chéo của hai hình chữ nhật bằng nhau) (2)

Từ (1) và (2) suy ra $ABGH$ là hình bình hành, suy ra $AH//BG$.

$AH//BG$ mà $BG\subset mp\left(BCGF\right)$, suy ra $AH//mp\left(BCGF\right)$.