Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 111, 112, 113 Bài 1: Hình hộp chữ nhật chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 111, 112, 113 Toán 8 Bài1: Hình hộp chữ nhật
Câu hỏi Vở bài tập Toán 8 trang 111 - 113: Khoanh tròn vào chữ cái trước khẳng định đúng.
Câu 1
Hình hộp chữ nhật có số mặt hình chữ nhật là:
A. B.
C. D.
Phương pháp giải:
Sử dụng kiến thức về hình hộp chữ nhật: Có mặt, đỉnh, cạnh.
Lời giải:
Hình hộp chữ nhật có mặt đều là các hình chữ nhật.
Chọn B.
Câu 2
Hình hộp chữ nhật có số cạnh là:
A. B.
C. D.
Phương pháp giải:
Sử dụng kiến thức về hình hộp chữ nhật: Có mặt, đỉnh, cạnh.
Lời giải:
Hình hộp chữ nhật có cạnh.
Chọn A.
Câu 3
Hình hộp chữ nhật có số đỉnh là:
A. B.
C. D.
Phương pháp giải:
Sử dụng kiến thức về hình hộp chữ nhật: Có mặt, đỉnh, cạnh.
Lời giải:
Hình hộp chữ nhật có đỉnh.
Chọn C.
Vở bài tập Toán 8 trang 111 - 113 Bài 1: Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật ABCD.MNPQ.
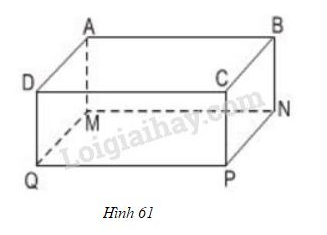
Phương pháp giải: Sử dụng kiến thức về hình hộp chữ nhật.
Lời giải:
- Bốn cạnh thứ nhất bằng nhau là:
- Bốn cạnh thứ hai bằng nhau là:
- Bốn cạnh thứ ba bằng nhau là:
Vở bài tập Toán 8 trang 111 - 113 Bài 2: là một hình hộp chữ nhật
a) Nếu là trung điểm của đoạn thì có là điểm thuộc đoạn hay không ?
b) là điểm thuộc cạnh , liệu có thể là điểm thuộc cạnh hay không?
Phương pháp giải: Áp dụng tính chất của hình hộp chữ nhật.
Lời giải:
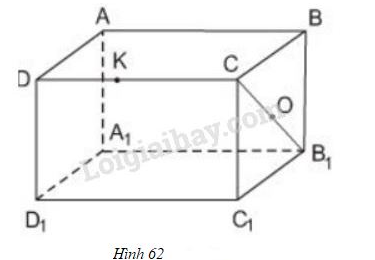
a) Tứ giác là hình chữ nhật nên hai đường chéo và phải cắt nhau tại .
Do đó nếu là trung điểm của đoạn thì cũng là trung điểm của đoạn .
Suy ra thuộc đoạn .
b) và là hai mặt đối diện của hình hộp , do đó chúng không có cạnh chung.
- Điểm thuộc cạnh của mặt nên không thể thuộc mặt , do đó càng không thể thuộc cạnh , vì nằm trong mặt
Vở bài tập Toán 8 trang 111 - 113 Bài 3: Các kích thước của hình hộp chữ nhật là . Hỏi độ dài và là bao nhiêu xentimét?
Phương pháp giải: Áp dụng các tính chất của hình hộp chữ nhật, định lí pitago
Lời giải:
mà nên .
là hình chữ nhật, do đó là tam giác vuông tại .
Theo định lí Py – ta – go, ta có:
cũng là hình chữ nhật nên là tam giác vuông tại .
Theo định lí Py – ta – go, ta có:
.
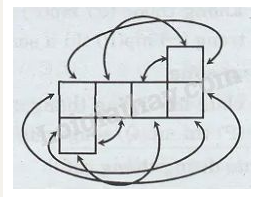
Vở bài tập Toán 8 trang 111 - 113 Bài 4: Xem hình 64a, các mũi tên hướng dẫn cách ghép các cạnh với nhau để có được một hình lập phương. Hãy điền thêm vào hình 64b các mũi tên như vậy.
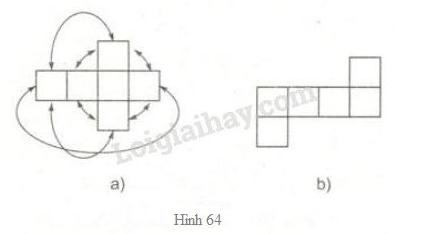
Phương pháp giải: Áp dụng định nghĩa hình lập phương.
Lời giải:
Hướng dẫn chung:
Để ghép được đúng các cặp cạnh với nhau, cần chú ý thực hiện các bước sau:
- Trước hết hãy xác định các cặp mặt đối diện với nhau (Thí dụ: mặt gạch sọc ở hình 65)
- Coi hai mặt đối diện nào đó là đáy trên và đáy dưới thì các mặt còn lại là các mặt bên.
- Chú ý rằng, các mặt đối diện thì không có cạnh chung, do đó không thể ghép các cạnh của hai mặt đối diện với nhau.
- Trước hết, hãy ghép các cạnh của ba mặt chung đỉnh với nhau, rồi từ đó tưởng tượng để ghép hai cạnh của ba mặt chung đỉnh tiếp theo.
- Hai cạnh ngoài cùng của hình chữ nhật ô vuông luôn được ghép với nhau.
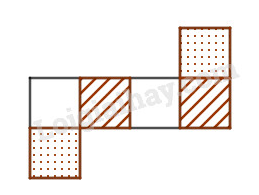
Các em có thể ghép theo hình mũi tên sau: