Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 117, 118, 119, 120, 121 Bài 3: Thể tích của hình hộp chữ nhật trang 117, 118, 119, 120, 121 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 117, 118, 119, 120, 121 Bài 3: Thể tích của hình hộp chữ nhật
Câu hỏi Vở bài tập Toán 8 trang 117 - 121:
Câu 8. Đúng ghi Đ, sai ghi S vào ô trống trong mỗi mệnh đề sau:

Phương pháp giải:
Sử dụng lý thuyết về đường thẳng vuông góc với mặt phẳng.
Lời giải:
a) Sai vì hai đường thẳng và cần bổ sung điều kiện cắt nhau.
b) Đúng.
Ta điền như sau:

Câu 9. Một hình hộp chữ nhật có các kích thước là: 5,3cm; 4,7cm và 7,5cm.
a) Thể tích của hình hộp chữ nhật nói trên (tính chính xác đến hai chữ số thập phân) là:
A. B.
C. D.
Khoanh tròn vào chữ cái trước khẳng định đúng.
b) Một hình lập phương có độ dài cạnh bằng trung bình cộng các kích thước của hình hộp chữ nhật nói trên, có thể tích (lấy chính xác đến hai chữ số thập phân) là:
A. B.
C. D.
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
- Thể tích hình hộp chữ nhật .
- Thể tích hình lập phương
Lời giải
a) Thể tích hình hộp là .
Chọn B.
b) Cạnh hình lập phương là
Thể tích hình lập phương là: .
Chọn A.
Vở bài tập Toán 8 trang 117 - 121 Bài 9:
a, Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với và thể tích của hình hộp này là .
b, Diện tích toàn phần của một hình lập phương là . Thể tích của nó bằng bao nhiêu?
Phương pháp giải:
a, Áp dụng công thức tính thể tích hình hộp chữ nhật : , trong đó là ba kích thước của hình hộp chữ nhật. Sau đó áp dụng tính chất của tỉ lệ thức để tìm .
b,
Diện tích toàn phần = diện tích một mặt
Do đó, diện tích một mặt = diện tích toàn phần
Lập luận để tìm độ dài cạnh hình lập phương.
Áp dụng công thức tính diện tích hình lập phương : .
Lời giải:
a,
Gọi các kích thước của một hình hộp chữ nhật tỉ lệ với theo thứ tự là: ta có:
Tính cạnh theo cạnh , ta có:
Theo công thức tính thể tích của hình hộp chữ nhật, ta có:
.
Theo giả thiết nên ta có:
Tính theo ta có: ;
b,
Diện tích toàn phần của hình lập phương là tổng diện tích mặt hình vuông của nó.
Gọi là cạnh của hình lập phương, ta có:
Thể tích của hình lập phương là: .
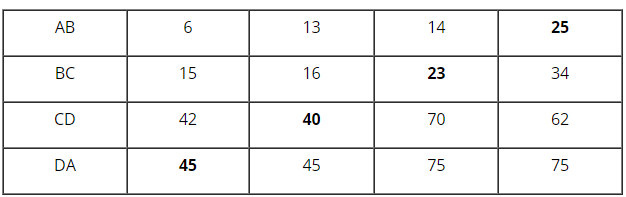
Vở bài tập Toán 8 trang 117 - 121 Bài 10: và là những đỉnh của hình hộp chữ nhật cho ở hình 70
Hãy điền số thích hợp vào các ô trống ở bảng sau:
Kết quả bài 10 minh họa công thức quan trọng sau:
Phương pháp giải:
- Áp dụng định lý Py-ta-go trong tam giác vuông để chứng minh công thức:
- Áp dụng công thức bên trên để tìm độ dài các đoạn thẳng chưa biết
Lời giải:
Trước hết ta chứng minh hệ thức sau:
Ta có : vuông tại
vuông tại
Suy ra:
Áp dụng hệ thức này ta sẽ tính được độ dài một cạnh khi biết ba độ dài kia.
Cột 1:
Cột 2:
Cột 3:
Cột 4:
Do đó ta có kết quả như bảng dưới đây:
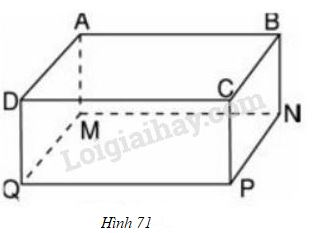
Vở bài tập Toán 8 trang 117 - 121 Bài 11:
a, Viết công thức tính thể tích của hình hộp chữ nhật (h71)
b, Điền số thích hợp vào các ô trống ở bảng sau: 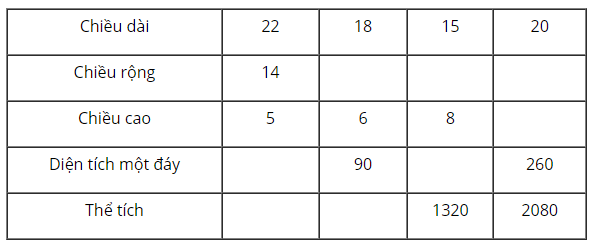
Phương pháp giải:a,
Áp dụng công thức tính thể tích hình hộp chữ nhật: , trong đó là các kích thước của hình hộp chữ nhật;
hay thể tích = chiều dài chiều rộng chiều cao.
b,
Giả sử là chiều dài, là chiều rộng và là chiều cao.
Ta áp dụng các công thức sau :
; ;
;
;
Lời giải:
a,
b,
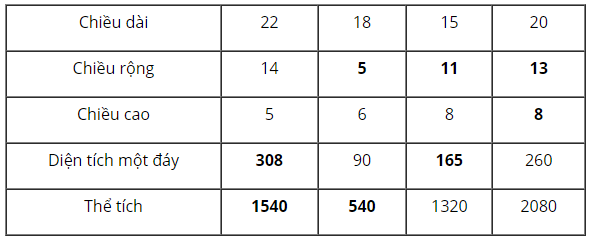
+ Hình hộp chữ nhật với các kích thước ở cột 1:
Diện tích một đáy là:
Thể tích là:
+ Hình hộp chữ nhật với các kích thước ở cột 2:
Chiều rộng là:
Thể tích là:
+ Hình hộp chữ nhật với các kích thước ở cột 3:
Chiều rộng là:
Diện tích một đáy là:
+ Hình hộp chữ nhật với các kích thước ở cột 4:
Chiều rộng là:
Chiều cao là:
Ta có kết quả chung như bảng sau:
Vở bài tập Toán 8 trang 117 - 121 Bài 12: Một bể nước hình hộp chữ nhật có chiều dài . Lúc đầu bể không có nước. Sau khi đổ vào bể thùng nước, mỗi thùng chứa lít thì mực nước của bể cao .
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm vào bể thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?
Phương pháp giải:
Giả sử
là chiều dài,
là chiều rộng và
là chiều cao.
Ta áp dụng các công thức sau:
; ;
Lời giải:
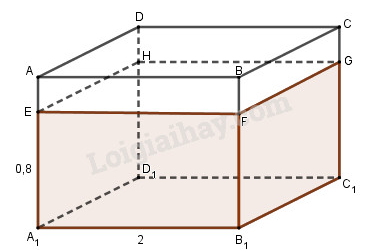
a) Giả sử bể nước là hình hộp chữ nhật có chiều dài là (h.72).
Chú ý: .
Sau khi đổ vào bể thùng nước, số nước đó được chứa đầy trong hình hộp chữ nhật có chiều cao .
Vậy ta có:
b) Sau khi đổ thêm thùng nước vào bể thì bể đầy, do đó thể tích bể là:
Vậy ta có:
Tính được:
Vở bài tập Toán 8 trang 117 - 121 Bài 13: Một cái thùng hình lập phương, cạnh , có chứa nước với độ sâu của nước là . Người ta thả viên gạch có chiều dài , chiều rộng và chiều cao vào thùng. Hỏi nước trong thùng dâng lên cách miệng thùng bao nhiêu đề-xi-mét? (Giả thiết toàn bộ gạch ngập trong nước và chúng hút nước không đáng kể).
Phương pháp giải:
- Tính thể tích nước đã có trong thùng, tức là tính thể tích của hình hộp chữ nhật có chiều dài , chiều rộng và chiều cao
- Tính thể tích của viên gạch, tức là tìm lần thể tích hình hộp chữ nhật có chiều dài , chiều rộng và chiều cao
- Tính thể tích của nước và gạch.
- Tính chiều cao mực nước trong thùng sau khi thả viên gạch = thể tích của nước và gạch: diện tích đáy.
- Khoảng cách giữa nước và miệng thùng = chiều cao của thùng - chiều cao mực nước trong thùng sau khi thả viên gạch.
Lời giải:
Giả sử thùng hình lập phương, có hình vẽ như hình dưới đây
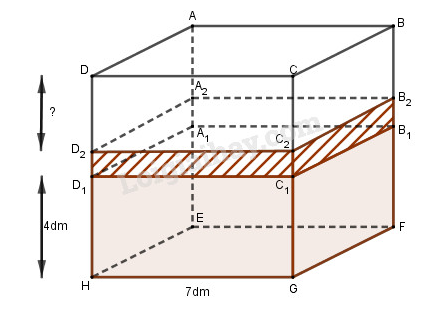
Khi chưa cho gạch vào, độ sâu của nước là . Khi thả viên gạch ngập trong nước, độ sâu của nước là . Khi đó nước dâng lên cách miệng thùng là . Ta phải tính .
Thể tích của viên gạch chính bằng thể tích nước dâng cao từ đến , do đó ta có:
.
Ta có:
Vậy nước dâng lên cách miệng thùng là
Vở bài tập Toán 8 trang 117 - 121 Bài 14: Cho hình hộp chữ nhật (h.74):
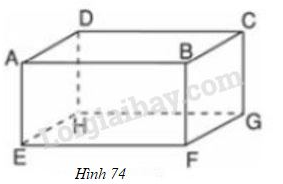
a) Kể tên các đường thẳng song song với mp .
b) Đường thẳng song song với những mặt phẳng nào?
c) Đường thẳng song song với những đường thẳng nào?
Phương pháp giải: Áp dụng lý thuyết về đường thẳng song song với mặt phẳng, hai đường thẳng song song.
Lời giải:
Các mặt của hình hộp chữ nhật đều là hình chữ nhật, do đó ra có:
- mà , do đó
- mà , do đó
- mà , do đó
- mà , do đó
Vậy các đường thẳng đều song song với .
b) mà , do đó
mà , do đó
Vậy song song với và
c) Trong , (1)
Trong , (2)
Trong , (3)
Từ (1),(3): và , do đó .
Vậy song song với các đường thẳng và .

