SBT Toán 8 Bài 5: Phép cộng phân thức đại số

SBT Toán 8 Bài 5: Phép cộng phân thức đại số | Giải SBT Toán lớp 8

Nghiêm Thị Ngà Ngày: 19-05-2022 Lớp 8

513

Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 5: Phép cộng phân thức đại số chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 5: Phép cộng phân thức đại số

Bài 17 Trang 28 SBT Toán 8 Tập 1: Cộng các phân thức cùng mẫu thức

a) $\frac{1 - 2 x}{6 x^{3} y} + \frac{3 + 2 y}{6 x^{3} y} + \frac{2 x - 4}{6 x^{3} y}$

b) $\frac{x^{2} - 2}{x {(x - 1)}^{2}} + \frac{2 - x}{x {(x - 1)}^{2}}$

c) $\frac{3 x + 1}{x^{2} - 3 x + 1} + \frac{x^{2} - 6 x}{x^{2} - 3 x + 1}$

d) $\frac{x^{2} + 38 x + 4}{2 x^{2} + 17 x + 1} + \frac{3 x^{2} - 4 x - 2}{2 x^{2} + 17 x + 1}$

Phương pháp giải:

Quy tắc: Muốn cộng hai phân thức cùng mẫu thức ta cộng các tử thức với nhau, giữ nguyên mẫu thức.

$\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

Lời giải:

a) $\frac{1 - 2 x}{6 x^{3} y} + \frac{3 + 2 y}{6 x^{3} y} + \frac{2 x - 4}{6 x^{3} y}$

$= \frac{1 - 2 x + 3 + 2 y + 2 x - 4}{6 x^{3} y}$ $= \frac{2 y}{6 x^{3} y} = \frac{1}{3 x^{3}}$

b) $\frac{x^{2} - 2}{x {(x - 1)}^{2}} + \frac{2 - x}{x {(x - 1)}^{2}}$

$= \frac{x^{2} - 2 + 2 - x}{x {(x - 1)}^{2}} = \frac{x^{2} - x}{x {(x - 1)}^{2}}$ $= \frac{x (x - 1)}{x {(x - 1)}^{2}} = \frac{1}{x - 1}$

c) $\frac{3 x + 1}{x^{2} - 3 x + 1} + \frac{x^{2} - 6 x}{x^{2} - 3 x + 1}$

$= \frac{3 x + 1 + x^{2} - 6 x}{x^{2} - 3 x + 1} = \frac{x^{2} - 3 x + 1}{x^{2} - 3 x + 1}$ $= 1$

d) $\frac{x^{2} + 38 x + 4}{2 x^{2} + 17 x + 1} + \frac{3 x^{2} - 4 x - 2}{2 x^{2} + 17 x + 1}$

$= \frac{x^{2} + 38 x + 4 + 3 x^{2} - 4 x - 2}{2 x^{2} + 17 x + 1}$

$= \frac{4 x^{2} + 34 x + 2}{2 x^{2} + 17 x + 1}$

$= \frac{2 (2 x^{2} + 17 x + 1)}{2 x^{2} + 17 x + 1} = 2$

Bài 18 Trang 28 SBT Toán 8 Tập 1: Cộng các phân thức khác mẫu thức:

a) $\frac{5}{6 x^{2} y} + \frac{7}{12 x y^{2}} + \frac{11}{18 x y}$

b) $\frac{4 x + 2}{15 x^{3} y} + \frac{5 y - 3}{9 x^{2} y} + \frac{x + 1}{5 x y^{3}}$

c) $\frac{3}{2 x} + \frac{3 x - 3}{2 x - 1} + \frac{2 x^{2} + 1}{4 x^{2} - 2 x}$

d) $\frac{x^{3} + 2 x}{x^{3} + 1} + \frac{2 x}{x^{2} - x + 1} + \frac{1}{x + 1}$

Phương pháp giải:

Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

$\frac{A}{B} + \frac{C}{D} = \frac{A D}{B D} + \frac{C B}{D B}$ $= \frac{A D + B C}{B D}$

Lời giải:

$= \frac{6 y^{2} + 25 x y^{3} - 3 x y^{2} + 9 x^{3} + 9 x^{2}}{45 x^{3} y^{3}}$

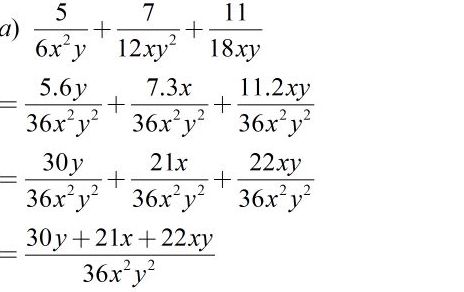
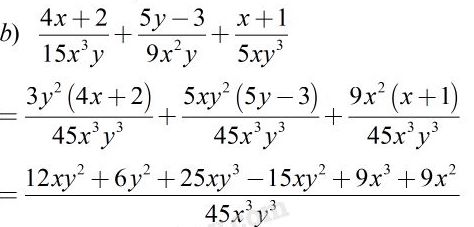
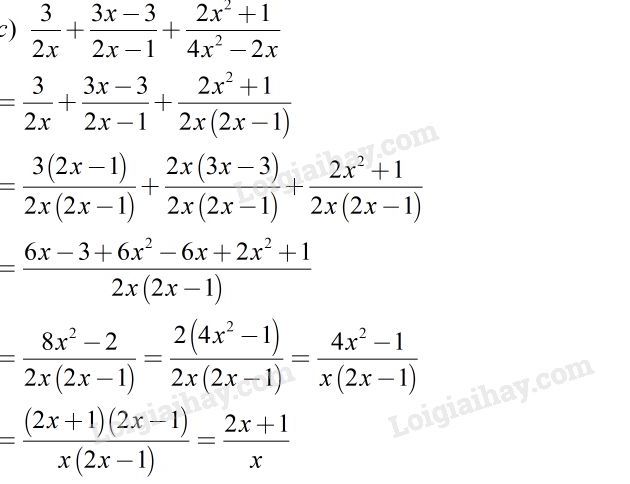
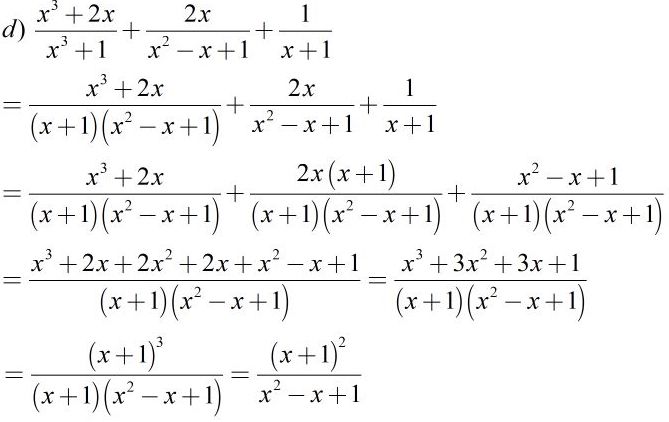
Bài 19 Trang 29 SBT Toán 8 Tập 1: Dùng quy tắc đổi dấu để tìm mẫu thức chung rồi thực hiện phép cộng:

a) $\frac{4}{x + 2} + \frac{2}{x - 2} + \frac{5 x - 6}{4 - x^{2}}$

b) $\frac{1 - 3 x}{2 x} + \frac{3 x - 2}{2 x - 1} + \frac{3 x - 2}{2 x - 4 x^{2}}$

c) $\frac{1}{x^{2} + 6 x + 9} + \frac{1}{6 x - x^{2} - 9} + \frac{x}{x^{2} - 9}$

d) $\frac{x^{2} + 2}{x^{3} - 1} + \frac{2}{x^{2} + x + 1} + \frac{1}{1 - x}$

e) $\frac{x}{x - 2 y} + \frac{x}{x + 2 y} + \frac{4 x y}{4 y^{2} - x^{2}}$

Phương pháp giải:

Sử dụng:

+) $A = - (- A)$

+) Quy đồng đưa về cộng các phân thức cùng mẫu thức $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

Lời giải:

a) $\frac{4}{x + 2} + \frac{2}{x - 2} + \frac{5 x - 6}{4 - x^{2}}$

$= \frac{4}{x + 2} + \frac{2}{x - 2} + \frac{5 x - 6}{- (x + 2) (x - 2)}$

$= \frac{4 (x - 2)}{(x + 2) (x - 2)}$ $+ \frac{2 (x + 2)}{(x + 2) (x - 2)}$ $+ \frac{6 - 5 x}{(x + 2) (x - 2)}$

$= \frac{4 x - 8 + 2 x + 4 + 6 - 5 x}{(x + 2) (x - 2)}$

$= \frac{x + 2}{(x + 2) (x - 2)} = \frac{1}{x - 2}$

b) $\frac{1 - 3 x}{2 x} + \frac{3 x - 2}{2 x - 1} + \frac{3 x - 2}{2 x - 4 x^{2}}$

$= \frac{1 - 3 x}{2 x} + \frac{3 x - 2}{2 x - 1} + \frac{2 - 3 x}{4 x^{2} - 2 x}$

$= \frac{1 - 3 x}{2 x} + \frac{3 x - 2}{2 x - 1} + \frac{2 - 3 x}{2 x (2 x - 1)}$

$= \frac{(1 - 3 x) (2 x - 1)}{2 x (2 x - 1)}$ $+ \frac{(3 x - 2) .2 x}{2 x (2 x - 1)}$ $+ \frac{2 - 3 x}{2 x (2 x - 1)}$ $= \frac{2 x - 1 - 6 x^{2} + 3 x + 6 x^{2} - 4 x + 2 - 3 x}{2 x (2 x - 1)}$ $= \frac{1 - 2 x}{2 x (2 x - 1)}$ $= \frac{- (2 x - 1)}{2 x (2 x - 1)}$ $= \frac{- 1}{2 x}$

c) $\frac{1}{x^{2} + 6 x + 9} + \frac{1}{6 x - x^{2} - 9}$ $+ \frac{x}{x^{2} - 9}$ $= \frac{1}{{(x + 3)}^{2}} + \frac{- 1}{{(x - 3)}^{2}}$ $+ \frac{x}{(x + 3) (x - 3)}$

$= \frac{{(x - 3)}^{2}}{{(x + 3)}^{2} {(x - 3)}^{2}}$ $+ \frac{- {(x + 3)}^{2}}{{(x + 3)}^{2} {(x - 3)}^{2}}$ $+ \frac{x (x + 3) (x - 3)}{{(x + 3)}^{2} {(x - 3)}^{2}}$ $= \frac{x^{2} - 6 x + 9 - x^{2} - 6 x - 9 + x^{3} - 9 x}{{(x + 3)}^{2} {(x - 3)}^{2}}$ $= \frac{x^{3} - 21 x}{{(x + 3)}^{2} {(x - 3)}^{2}}$

d) $\frac{x^{2} + 2}{x^{3} - 1} + \frac{2}{x^{2} + x + 1} + \frac{1}{1 - x}$ $= \frac{x^{2} + 2}{(x - 1) (x^{2} + x + 1)}$ $+ \frac{2}{x^{2} + x + 1} + \frac{- 1}{x - 1}$

$= \frac{x^{2} + 2}{(x - 1) (x^{2} + x + 1)}$ $+ \frac{2 (x - 1)}{(x - 1) (x^{2} + x + 1)}$ $+ \frac{- (x^{2} + x + 1)}{(x - 1) (x^{2} + x + 1)}$ $= \frac{x^{2} + 2 + 2 x - 2 - x^{2} - x - 1}{(x - 1) (x^{2} + x + 1)}$ $= \frac{x - 1}{(x - 1) (x^{2} + x + 1)}$ $= \frac{1}{x^{2} + x + 1}$

e) $\frac{x}{x - 2 y} + \frac{x}{x + 2 y} + \frac{4 x y}{4 y^{2} - x^{2}}$

$= \frac{x}{x - 2 y} + \frac{x}{x + 2 y} + \frac{- 4 x y}{x^{2} - 4 y^{2}}$

$= \frac{x}{x - 2 y} + \frac{x}{x + 2 y}$ $+ \frac{- 4 x y}{(x + 2 y) (x - 2 y)}$

$= \frac{x (x + 2 y)}{(x - 2 y) (x + 2 y)}$ $+ \frac{x (x - 2 y)}{(x - 2 y) (x + 2 y)}$ $+ \frac{- 4 x y}{(x - 2 y) (x + 2 y)}$ $= \frac{x^{2} + 2 x y + x^{2} - 2 x y - 4 x y}{(x - 2 y) (x + 2 y)}$ $= \frac{2 x^{2} - 4 x y}{(x - 2 y) (x + 2 y)}$ $= \frac{2 x (x - 2 y)}{(x - 2 y) (x + 2 y)}$ $= \frac{2 x}{x + 2 y}$

Bài 20 Trang 29 SBT Toán 8 Tập 1: Cộng các phân thức:

a) $\frac{1}{(x - y) (y - z)}$ + $\frac{1}{(y - z) (z - x)}$ + $\frac{1}{(z - x) (x - y)}$

b) $\frac{4}{(y - x) (z - x)} + \frac{3}{(y - x) (y - z)}$ + $\frac{3}{(y - z) (x - z)}$

c) $\frac{1}{x (x - y) (x - z)} + \frac{1}{y (y - z) (y - x)}$ + $\frac{1}{z (z - x) (z - y)}$

Phương pháp giải:

Quy tắc: Muốn cộng hai phân thức có mẫu thức khác nhau ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.

$\frac{A}{B} + \frac{C}{D} = \frac{A D}{B D} + \frac{C B}{D B}$ $= \frac{A D + B C}{B D}$

Lời giải:

a) $\frac{1}{(x - y) (y - z)} + \frac{1}{(y - z) (z - x)}$ + $\frac{1}{(z - x) (x - y)}$

$= \frac{z - x}{(x - y) (y - z) (z - x)}$ $+ \frac{x - y}{(x - y) (y - z) (z - x)}$ $+ \frac{y - z}{(x - y) (y - z) (z - x)}$ $= \frac{z - x + x - y + y - z}{(x - y) (y - z) (z - x)} = 0$

b) $\frac{4}{(y - x) (z - x)}$ $+ \frac{3}{(y - x) (y - z)}$ $+ \frac{3}{(y - z) (x - z)}$

$= \frac{- 4}{(y - x) (x - z)}$ $+ \frac{3}{(y - x) (y - z)}$ $+ \frac{3}{(y - z) (x - z)}$

$= \frac{- 4 (y - z)}{(x - z) (y - z) (y - x)}$ $+ \frac{3 (x - z)}{(x - z) (y - z) (y - x)}$ $+ \frac{3 (y - x)}{(x - z) (y - z) (y - x)}$

$= \frac{- 4 y + 4 z + 3 x - 3 z + 3 y - 3 x}{(x - z) (y - z) (y - x)}$ $= \frac{z - y}{(x - z) (y - z) (y - x)}$

$= \frac{- (y - z)}{(x - z) (y - z) (y - x)}$ $= \frac{- 1}{(x - z) (y - x)} = \frac{1}{(x - z) (x - y)}$

c) $\frac{1}{x (x - y) (x - z)}$ $+ \frac{1}{y (y - z) (y - x)}$ $+ \frac{1}{z (z - x) (z - y)}$

$= \frac{1}{x (x - y) (x - z)}$ $+ \frac{- 1}{y (x - y) (y - z)}$ $+ \frac{1}{z (x - z) (y - z)}$

$= \frac{y z (y - z)}{x y z (x - y) (x - z) (y - z)}$ $+ \frac{- x z (x - z)}{x y z (x - y) (x - z) (y - z)}$ $+ \frac{x y (x - y)}{x y z (x - y) (x - z) (y - z)}$

$= \frac{y^{2} z - y z^{2} - x^{2} z + x z^{2} + x^{2} y - x y^{2}}{x y z (x - y) (x - z) (y - z)}$

$= \frac{(x z^{2} - y z^{2}) + (x^{2} y - x y^{2}) - (x^{2} z - y^{2} z)}{x y z (x - y) (x - z) (y - z)}$

$= \frac{z^{2} (x - y) + x y (x - y) - z (x - y) (x + y)}{x y z (x - y) (x - z) (y - z)}$ $= \frac{(x - y) (z^{2} + x y - x z - y z)}{x y z (x - y) (x - z) (y - z)}$ $= \frac{(x - y) [x (y - z) - z (y - z)]}{x y z (x - y) (x - z) (y - z)}$ $= \frac{(x - y) (y - z) (x - z)}{x y z (x - y) (x - z) (y - z)} = \frac{1}{x y z}$

Bài 21 Trang 29 SBT Toán 8 Tập 1: Làm tính cộng các phân thức

a) $\frac{11 x + 13}{3 x - 3} + \frac{15 x + 17}{4 - 4 x}$

b) $\frac{2 x + 1}{2 x^{2} - x} + \frac{32 x^{2}}{1 - 4 x^{2}} + \frac{1 - 2 x}{2 x^{2} + x}$

c) $\frac{1}{x^{2} + x + 1} + \frac{1}{x^{2} - x} + \frac{2 x}{1 - x^{3}}$

d) $\frac{x^{4}}{1 - x} + x^{3} + x^{2} + x + 1$

Phương pháp giải:

+ Quy đồng mẫu thức các phân thức

+ Đưa về cộng các phân thức cùng mẫu: $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

Lời giải:

a) $\frac{11 x + 13}{3 x - 3} + \frac{15 x + 17}{4 - 4 x}$

$= \frac{11 x + 13}{3 x - 3} + \frac{- (15 x + 17)}{4 x - 4}$

$= \frac{11 x + 13}{3 (x - 1)} + \frac{- 15 x - 17}{4 (x - 1)}$

$= \frac{4 (11 x + 13)}{12 (x - 1)} + \frac{3 (- 15 x - 17)}{12 (x - 1)}$ $= \frac{44 x + 52 - 45 x - 51}{12 (x - 1)}$ $= \frac{1 - x}{12 (x - 1)}$ $= \frac{- (x - 1)}{12 (x - 1)} = - \frac{1}{12}$

b) $\frac{2 x + 1}{2 x^{2} - x} + \frac{32 x^{2}}{1 - 4 x^{2}} + \frac{1 - 2 x}{2 x^{2} + x}$

$= \frac{2 x + 1}{2 x^{2} - x} + \frac{- 32 x^{2}}{4 x^{2} - 1} + \frac{1 - 2 x}{2 x^{2} + x}$

$= \frac{2 x + 1}{x (2 x - 1)}$ $+ \frac{- 32 x^{2}}{(2 x + 1) (2 x - 1)}$ $+ \frac{1 - 2 x}{x (2 x + 1)}$

$= \frac{(2 x + 1) (2 x + 1)}{x (2 x + 1) (2 x - 1)}$ $+ \frac{- 32 x^{2} . x}{x (2 x + 1) (2 x - 1)}$ $+ \frac{(1 - 2 x) (2 x - 1)}{x (2 x + 1) (2 x - 1)}$ $= \frac{4 x^{2} + 4 x + 1 - 32 x^{3} + 2 x - 1 - 4 x^{2} + 2 x}{x (2 x + 1) (2 x - 1)}$ $= \frac{- 32 x^{3} + 8 x}{x (2 x + 1) (2 x - 1)}$ $= \frac{- 8 x (4 x^{2} - 1)}{x (2 x + 1) (2 x - 1)}$ $= \frac{- 8 x (2 x + 1) (2 x - 1)}{x (2 x + 1) (2 x - 1)} = - 8$

c) $\frac{1}{x^{2} + x + 1} + \frac{1}{x^{2} - x} + \frac{2 x}{1 - x^{3}}$

$\frac{1}{x^{2} + x + 1} + \frac{1}{x^{2} - x} + \frac{- 2 x}{x^{3} - 1}$

$= \frac{1}{x^{2} + x + 1} + \frac{1}{x (x - 1)}$ $+ \frac{- 2 x}{(x - 1) (x^{2} + x + 1)}$

$= \frac{x (x - 1)}{x (x - 1) (x^{2} + x + 1)}$ $+ \frac{x^{2} + x + 1}{x (x - 1) (x^{2} + x + 1)}$ $+ \frac{- 2 x . x}{x (x - 1) (x^{2} + x + 1)}$ $= \frac{x^{2} - x + x^{2} + x + 1 - 2 x^{2}}{x (x - 1) (x^{2} + x + 1)}$ $= \frac{1}{x (x^{3} - 1)}$

d) $\frac{x^{4}}{1 - x} + x^{3} + x^{2} + x + 1$ $= \frac{x^{4}}{1 - x}$ $+ \frac{(x^{3} + x^{2} + x + 1) (1 - x)}{1 - x}$

$= \frac{x^{4} + x^{3} + x^{2} + x + 1 - x^{4} - x^{3} - x^{2} - x}{1 - x}$ $= \frac{1}{1 - x}$

Bài 22 Trang 29 SBT Toán 8 Tập 1

: Cho hai biểu thức:

$A = \frac{1}{x} + \frac{1}{x + 5} + \frac{x - 5}{x (x + 5)}$

$B = \frac{3}{x + 5}$

Chứng tỏ rằng $A = B .$

Phương pháp giải:

+ Quy đồng mẫu thức các phân thức

+ Đưa về cộng các phân thức cùng mẫu: $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

Lời giải:

Ta có:

$A = \frac{1}{x} + \frac{1}{x + 5} + \frac{x - 5}{x (x + 5)}$ $= \frac{x + 5}{x (x + 5)} + \frac{x}{x (x + 5)} + \frac{x - 5}{x (x + 5)}$

$= \frac{x + 5 + x + x - 5}{x (x + 5)}$ $= \frac{3 x}{x (x + 5)} = \frac{3}{x + 5} = B$

Vậy $A = B .$

Bài 23 Trang 29 SBT Toán 8 Tập 1: Con tàu du lịch “Sông Hồng” đưa khách từ Hà Nội đến Việt Trì. Sau đó, nó nghỉ lại tại Việt Trì $2$ giờ rồi quay về Hà Nội. Độ dài khúc sông từ Hà Nội đến Việt Trì là $70 k m .$ Vận tốc của dòng nước là $5 k m / h .$ Vận tốc thực của con tàu (tức là vận tốc trong nước yên lặng) là $x$ km/h.

a) Hãy biểu diễn qua x :

- Thời gian ngược từ Hà Nội đến Việt Trì;

- Thời gian xuôi từ Việt Trì về Hà Nội;

- Thời gian kể từ lúc xuất phát đến khi về tới Hà Nội.

b) Tính thời gian kể từ lúc xuất phát đến khi con tàu về tới Hà Nội, biết rằng vận tốc lúc ngược dòng của con tàu là 20 km/h.

Phương pháp giải:

a) Sử dụng:

Thời gian = Quãng đường chia cho vận tốc

Vận tốc xuôi dòng = Vận tốc thực + vận tốc dòng nước

Vận tốc ngược dòng = Vận tốc thực - vận tốc dòng nước

b) Tính vận tốc xuôi dòng, vận tốc ngược dòng và thay vào $\frac{70}{x - 5} + 2 + \frac{70}{x + 5}$

Lời giải:

Vận tốc ngược dòng đi từ Hà Nội lên Việt Trì là $x - 5$ (km/h) nên thời gian đi từ Hà Nội đến Việt Trì là $\frac{70}{x - 5}$ (giờ)

Vận tốc từ Việt Trì về Hà Nội là vận tốc xuôi dòng bằng: $x + 5$ (km/h)

Thời gian đi từ Việt Trì về Hà Nội là $\frac{70}{x + 5}$ (giờ)

Thời gian từ lúc xuất phát đến khi trở về Hà Nội là :

$\frac{70}{x - 5} + 2 + \frac{70}{x + 5}$ $= \frac{70 (x + 5)}{(x - 5) (x + 5)}$ $+ \frac{2 (x + 5) (x - 5)}{(x - 5) (x + 5)}$ $+ \frac{70 (x - 5)}{(x - 5) (x + 5)}$ $= \frac{70 x + 350 + 2 x^{2} - 50 + 70 x - 350}{(x - 5) (x + 5)}$ $= \frac{2 x^{2} + 140 x - 50}{(x - 5) (x + 5)}$ (giờ)

b) Vận tốc lúc ngược dòng $x - 5 = 20 \Rightarrow x = 25$

Vận tốc lúc xuôi dòng là $25 + 5 = 30$

Thay vào $\frac{70}{x - 5} + 2 + \frac{70}{x + 5},$ ta có:

$\frac{70}{20} + 2 + \frac{70}{30}$ $= \frac{7}{2} + \frac{7}{3} + 2$ $= \frac{21}{6} + \frac{14}{6} + 2$ $= \frac{35}{6} + 2$ $= 7 \frac{5}{6}$

Bài 5.1 Trang 30 SBT Toán 8 Tập 1: Cộng hai phân thức $\frac{x + 3}{2 x - 1} + \frac{4 - x}{1 - 2 x}$ .

Phương án nào sau đây là đúng ?

A. $\frac{7}{2 x - 1}$

B. $\frac{7}{1 - 2 x}$

C. $1$

D. $- 1$

Phương pháp giải:

+) Sử dụng tính chất: $A = - (- A)$ để đưa về hai phân thức cùng mẫu

+) Muốn cộng các phân thức cùng mẫu: $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

Lời giải:

Ta có:

$\begin{array}{l} \frac{x + 3}{2 x - 1} + \frac{4 - x}{1 - 2 x} \\ = \frac{x + 3}{2 x - 1} + \frac{x - 4}{2 x - 1} \\ = \frac{x + 3 + x - 4}{2 x - 1} \\ = \frac{2 x - 1}{2 x - 1} \\ = 1 \end{array}$

Chọn C.

Bài 5.2 Trang 30 SBT Toán 8 Tập 1: Thực hiện phép cộng:

$\frac{1}{1 - x} + \frac{1}{1 + x}$ $+ \frac{2}{1 + x^{2}} + \frac{4}{1 + x^{4}}$ $+ \frac{8}{1 + x^{8}} + \frac{16}{1 + x^{16}}$

Phương pháp giải:

+ Quy đồng mẫu thức các phân thức

+ Đưa về cộng các phân thức cùng mẫu: $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$

+ Cộng lần lượt 2 phân thức đầu với nhau, bài này ta không quy đồng tất cả ngay từ đầu.

Lời giải:

$\frac{1}{1 - x} + \frac{1}{1 + x}$ $+ \frac{2}{1 + x^{2}}$ $+ \frac{4}{1 + x^{4}}$ $+ \frac{8}{1 + x^{8}}$ $+ \frac{16}{1 + x^{16}}$

$= \frac{1 + x + 1 - x}{(1 - x) (1 + x)} + \frac{2}{1 + x^{2}}$ $+ \frac{4}{1 + x^{4}} + \frac{8}{1 + x^{8}}$ $+ \frac{16}{1 + x^{16}}$ $= \frac{2}{1 - x^{2}} + \frac{2}{1 + x^{2}} + \frac{4}{1 + x^{4}}$ $+ \frac{8}{1 + x^{8}} + \frac{16}{1 + x^{16}}$