SBT Toán 8 Bài 4: Quy đồng mẫu thức nhiều phân thức

SBT Toán 8 Bài 4: Quy đồng mẫu thức nhiều phân thức | Giải SBT Toán lớp 8

Nghiêm Thị Ngà Ngày: 19-05-2022 Lớp 8

588

Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 4: Quy đồng mẫu thức nhiều phân thức chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 4: Quy đồng mẫu thức nhiều phân thức

Bài 13 Trang 27 SBT Toán 8 Tập 1: Quy đồng mẫu thức các phân thức:

a) $\frac{25}{14 x^{2} y}, \frac{14}{21 x y^{5}}$

b) $\frac{11}{102 x^{4} y}, \frac{3}{34 x y^{3}}$

c) $\frac{3 x + 1}{12 x y^{4}}, \frac{y - 2}{9 x^{2} y^{3}}$

d) $\frac{1}{6 x^{3} y^{2}}, \frac{x + 1}{9 x^{2} y^{4}}, \frac{x - 1}{4 x y^{3}}$

e) $\frac{3 + 2 x}{10 x^{4} y}, \frac{5}{8 x^{2} y^{2}}, \frac{2}{3 x y^{5}}$

f) $\frac{4 x - 4}{2 x (x + 3)}, \frac{x - 3}{3 x (x + 1)}$

g) $\frac{2 x}{{(x + 2)}^{3}}, \frac{x - 2}{2 x {(x + 2)}^{2}}$

h) $\frac{5}{3 x^{3} - 12 x}, \frac{3}{(2 x + 4) (x + 3)}$

Phương pháp giải:

Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải:

a) MTC $= 42 x^{2} y^{5}$

Nhân tử phụ thứ nhất là: $3 y^{4}$

Nhân tử phụ thứ hai là: $2 x$

Quy đồng:

$\frac{25}{14 x^{2} y} = \frac{25. 3 y^{4}}{14 x^{2} y . 3 y^{4}} = \frac{75 y^{4}}{42 x^{2} y^{5}};$

$\frac{14}{21 x y^{5}} = \frac{14.2 x}{21 x y^{5} .2 x} = \frac{28 x}{42 x^{2} y^{5}}$

b) MTC $= 102 x^{4} y^{3}$

Nhân tử phụ thứ nhất là: $y^{2}$

Nhân tử phụ thứ hai là: $3 x^{3}$ .

Quy đồng:

$\frac{11}{102 x^{4} y} = \frac{11. y^{2}}{102 x^{4} y . y^{2}} = \frac{11 y^{2}}{102 x^{4} y^{3}}$ ;

$\frac{3}{34 x y^{3}} = \frac{3.3 x^{3}}{34 x y^{3} .3 x^{3}} = \frac{9 x^{3}}{102 x^{4} y^{3}}$

c) MTC $= 36 x^{2} y^{4}$

Nhân tử phụ thứ nhất là: $3 x$

Nhân tử phụ thứ hai là: $4 y$

Quy đồng:

$\frac{3 x + 1}{12 x y^{4}} = \frac{(3 x + 1) .3 x}{12 x y^{4} .3 x} = \frac{9 x^{2} + 3 x}{36 x^{2} y^{4}}$ ;

$\frac{y - 2}{9 x^{2} y^{3}} = \frac{(y - 2) .4 y}{9 x^{2} y^{3} .4 y} = \frac{4 y^{2} - 8 y}{36 x^{2} y^{4}}$

d) MTC $= 36 x^{3} y^{4}$

Nhân tử phụ thứ nhất là: $6 y^{2}$

Nhân tử phụ thứ hai là: $4 x$

Nhân tử phụ thứ ba là: $9 x^{2} y$ .

Quy đồng:

$\frac{1}{6 x^{3} y^{2}} = \frac{1.6 y^{2}}{6 x^{3} y^{2} .6 y^{2}} = \frac{6 y^{2}}{36 x^{3} y^{4}}$ ;

$\frac{x + 1}{9 x^{2} y^{4}} = \frac{(x + 1) .4 x}{9 x^{2} y^{4} .4 x} = \frac{4 x^{2} + 4 x}{36 x^{3} y^{4}}$

$\frac{x - 1}{4 x y^{3}} = \frac{(x - 1) .9 x^{2} y}{4 x y^{3} .9 x^{2} y}$ $= \frac{9 x^{3} y - 9 x^{2} y}{36 x^{3} y^{4}}$

e) MTC $= 120 x^{4} y^{5}$

Nhân tử phụ thứ nhất là: $12 y^{4}$

Nhân tử phụ thứ hai là: $15 x^{2} y^{3}$

Nhân tử phụ thứ ba là: $40 x^{3}$ .

Quy đồng:

$\frac{3 + 2 x}{10 x^{4} y} = \frac{(3 + 2 x) .12 y^{4}}{10 x^{4} y .12 y^{4}}$ $= \frac{36 y^{4} + 24 x y^{4}}{120 x^{4} y^{5}}$

$\frac{5}{8 x^{2} y^{2}} = \frac{5.15 x^{2} y^{3}}{8 x^{2} y^{2} .15 x^{2} y^{3}} = \frac{75 x^{2} y^{3}}{120 x^{4} y^{5}}$

$\frac{2}{3 x y^{5}} = \frac{2.40 x^{3}}{3 x y^{5} .40 x^{3}} = \frac{80 x^{3}}{120 x^{4} y^{5}}$

f) Ta có: $\frac{4 x - 4}{2 x (x + 3)} = \frac{4 (x - 1)}{2 x (x + 3)}$ $= \frac{2 (x - 1)}{x (x + 3)}$

MTC $= 3 x (x + 3) (x + 1)$

Nhân tử phụ thứ nhất là: $3 (x + 1)$

Nhân tử phụ thứ hai là: $(x + 3)$

Quy đồng:

$\frac{4 x - 4}{2 x (x + 3)} = \frac{2 (x - 1)}{x (x + 3)}$ $= \frac{2 (x - 1) .3 (x + 1)}{x (x + 3) .3 (x + 1)}$ $= \frac{6 (x^{2} - 1)}{3 x (x + 3) (x + 1)}$

$\frac{x - 3}{3 x (x + 1)} = \frac{(x - 3) (x + 3)}{3 x (x + 1) (x + 3)}$ $= \frac{x^{2} - 9}{3 x (x + 1) (x + 3)}$

g) MTC $= 2 x {(x + 2)}^{3}$

Nhân tử phụ thứ nhất là: $2 x$

Nhân tử phụ thứ hai là: $(x + 2)$ .

Quy đồng:

$\frac{2 x}{{(x + 2)}^{3}} = \frac{2 x .2 x}{2 x {(x + 2)}^{3}}$ $= \frac{4 x^{2}}{2 x {(x + 2)}^{3}}$

$\frac{x - 2}{2 x {(x + 2)}^{2}} = \frac{(x - 2) (x + 2)}{2 x {(x + 2)}^{2} (x + 2)}$ $= \frac{x^{2} - 4}{2 x {(x + 2)}^{3}}$

h) $3 x^{3} - 12 x = 3 x (x^{2} - 4)$ $= 3 x (x - 2) (x + 2)$

$(2 x + 4) (x + 3) = 2 (x + 2) (x + 3)$

MTC = $6 x (x - 2) (x + 2) (x + 3)$

Nhân tử phụ thứ nhất là: $2 (x + 3)$

Nhân tử phụ thứ hai là: $3 x (x - 2)$ .

Quy đồng:

$\begin{aligned} \frac{5}{3 x^{3} - 12 x} = \frac{5}{3 x (x - 2) (x + 2)} \\ = \frac{5.2 (x + 3)}{3 x (x - 2) (x + 2) .2 (x + 3)} \\ = \frac{10 (x + 3)}{6 x (x - 2) (x + 2) (x + 3)} \\ \frac{3}{(2 x + 4) (x + 3)} \\ = \frac{3}{2 (x + 2) (x + 3)} \\ = \frac{3.3 x (x - 2)}{2 (x + 2) (x + 3) .3 x (x - 2)} \\ = \frac{9 x (x - 2)}{6 x (x + 2) (x - 2) (x + 3)} \end{aligned}$

Bài 14 Trang 27 SBT Toán 8 Tập 1: Quy đồng mẫu thức các phân thức:

a) $\frac{7 x - 1}{2 x^{2} + 6 x}, \frac{5 - 3 x}{x^{2} - 9}$

b) $\frac{x + 1}{x - x^{2}}, \frac{x + 2}{2 - 4 x + 2 x^{2}}$

c) $\frac{4 x^{2} - 3 x + 5}{x^{3} - 1}, \frac{2 x}{x^{2} + x + 1}, \frac{6}{x - 1}$

d) $\frac{7}{5 x}, \frac{4}{x - 2 y}, \frac{x - y}{8 y^{2} - 2 x^{2}}$

e) $\frac{5 x^{2}}{x^{3} + 6 x^{2} + 12 x + 8}, \frac{4 x}{x^{2} + 4 x + 4},$ $\frac{3}{2 x + 4}$

Phương pháp giải:

Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải:

a) $2 x^{2} + 6 x = 2 x (x + 3);$

$x^{2} - 9 = (x + 3) (x - 3)$

MTC $= 2 x (x + 3) (x - 3)$

$\frac{7 x - 1}{2 x^{2} + 6 x} = \frac{7 x - 1}{2 x (x + 3)}$ $= \frac{(7 x - 1) (x - 3)}{2 x (x + 3) (x - 3)}$

$\frac{5 - 3 x}{x^{2} - 9} = \frac{5 - 3 x}{(x + 3) (x - 3)}$ $= \frac{2 x (5 - 3 x)}{2 x (x + 3) (x - 3)}$

b) +) $x - x^{2} = x (1 - x)$ ;

+) $2 - 4 x + 2 x^{2} = 2 (1 - 2 x + x^{2})$ $= 2 {(1 - x)}^{2}$

MTC $= 2 x {(1 - x)}^{2}$

$\frac{x + 1}{x - x^{2}} = \frac{x + 1}{x (1 - x)}$ $= \frac{(x + 1) .2 (1 - x)}{x (1 - x) .2 (1 - x)} = \frac{2 (1 - x^{2})}{2 x {(1 - x)}^{2}}$

$\frac{x + 2}{2 - 4 x + 2 x^{2}} = \frac{x + 2}{2 {(1 - x)}^{2}}$ $= \frac{(x + 2) . x}{2 x {(1 - x)}^{2}}$

c) Ta có $x^{3} - 1 = (x - 1) (x^{2} + x + 1)$

MTC $= x^{3} - 1$

$\frac{4 x^{2} - 3 x + 5}{x^{3} - 1}$ ;

$\frac{2 x}{x^{2} + x + 1} = \frac{2 x (x - 1)}{(x^{2} + x + 1) (x - 1)}$ $= \frac{2 x (x - 1)}{x^{3} - 1}$

$\frac{6}{x - 1} = \frac{6 (x^{2} + x + 1)}{(x - 1) (x^{2} + x + 1)}$ $= \frac{6 (x^{2} + x + 1)}{x^{3} - 1}$

d) Ta có $8 y^{2} - 2 x^{2} = 2 (4 y^{2} - x^{2})$ $= 2 (2 y + x) (2 y - x)$

MTC $= 10 x (2 y + x) (2 y - x)$

$\frac{7}{5 x} = \frac{7.2 (2 y + x) (2 y - x)}{5 x .2 (2 y + x) (2 y - x)}$ $= \frac{14 (2 y + x) (2 y - x)}{10 x (2 y + x) (2 y - x)}$

$\frac{4}{x - 2 y} = \frac{- 4}{2 y - x}$ $= \frac{- 4.10 x (2 y + x)}{(2 y - x) .10 x (2 y + x)}$ $= \frac{- 40 x (2 y + x)}{10 x (2 y + x) (2 y - x)}$

$\frac{x - y}{8 y^{2} - 2 x^{2}} = \frac{x - y}{2 (2 y + x) (2 y - x)}$ $= \frac{(x - y) .5 x}{2 (2 y + x) (2 y - x) .5 x}$ $= \frac{5 x (x - y)}{10 x (2 y + x) (2 y - x)}$

e) Ta có $x^{3} + 6 x^{2} + 12 x + 8$ $= x^{3} + 3 x^{2} .2 + 3. x {.2}^{2} + 2^{3}$ $= {(x + 2)}^{3}$

$x^{2} + 4 x + 4 = {(x + 2)}^{2};$

$2 x + 4 = 2 (x + 2)$

MTC $= 2 {(x + 2)}^{3}$

$\frac{5 x^{2}}{x^{3} + 6 x^{2} + 12 x + 8} = \frac{5 x^{2}}{{(x + 2)}^{3}}$ $= \frac{5 x^{2} .2}{{(x + 2)}^{3} .2} = \frac{10 x^{2}}{2 {(x + 2)}^{3}}$

$\frac{4 x}{x^{2} + 4 x + 4} = \frac{4 x}{{(x + 2)}^{2}}$ $= \frac{4 x .2 (x + 2)}{{(x + 2)}^{2} .2 (x + 2)} = \frac{8 x (x + 2)}{2 {(x + 2)}^{3}}$

$\frac{3}{2 x + 4} = \frac{3}{2 (x + 2)}$ $= \frac{3 {(x + 2)}^{2}}{2 (x + 2) {(x + 2)}^{2}} = \frac{3 {(x + 2)}^{2}}{2 {(x + 2)}^{3}}$ .

Bài 15 Trang 28 SBT Toán 8 Tập 1: Cho đa thức $B = 2 x^{3} + 3 x^{2} - 29 x + 30$ và hai phân thức $\frac{x}{2 x^{2} + 7 x - 15}$ , $\frac{x + 2}{x^{2} + 3 x - 10}$

a) Chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho.

b) Quy đồng mẫu thức của hai phân thức đã cho.

Phương pháp giải:

a) Áp dụng quy tắc chia hai đa thức một biến.

b) Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải:

b) Áp dụng kết quả câu a) ta có:

MTC $= 2 x^{3} + 3 x^{2} - 29 x + 30$

$\frac{x}{2 x^{2} + 7 x - 15}$ $= \frac{x (x - 2)}{(2 x^{2} + 7 x - 15) (x - 2)}$ $= \frac{x^{2} - 2 x}{2 x^{3} + 3 x^{2} - 29 x + 30}$

$\frac{x + 2}{x^{2} + 3 x - 10}$ $= \frac{(x + 2) (2 x - 3)}{(x^{2} + 3 x - 10) (2 x - 3)}$ $= \frac{2 x^{2} + x - 6}{2 x^{3} + 3 x^{2} - 29 x + 30}$

Bài 16 Trang 28 SBT Toán 8 Tập 1: Cho hai phân thức $\frac{1}{x^{2} - 4 x - 5}$ và $\frac{2}{x^{2} - 2 x - 3}$

Chứng tỏ rằng có thể chọn đa thức $x^{3} - 7 x^{2} + 7 x + 15$ làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức.

Phương pháp giải:

Thực hiện phép chia đa thức $x^{3} - 7 x^{2} + 7 x + 15$ cho hai đa thức $x^{2} - 4 x - 5$ và $x^{2} - 2 x - 3$ . Nếu các phép chia đều là phép chia hết thì đa thức $x^{3} - 7 x^{2} + 7 x + 15$ là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.

Lời giải:

Ta có:

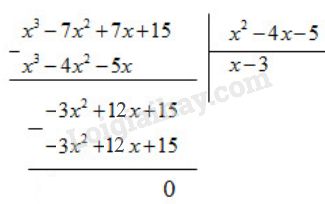
Suy ra: $x^{3} - 7 x^{2} + 7 x + 15$ $= (x^{2} - 4 x - 5) (x - 3)$

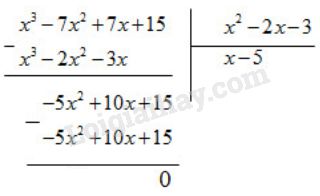
Suy ra: $x^{3} - 7 x^{2} + 7 x + 15$ $= (x^{2} - 2 x - 3) (x - 5)$

Vậy đa thức $x^{3} - 7 x^{2} + 7 x + 15$ là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.

* Quy đồng:

$\frac{1}{x^{2} - 4 x - 5}$

$= \frac{1. (x - 3)}{(x^{2} - 4 x - 5) . (x - 3)}$

$= \frac{x - 3}{x^{3} - 7 x^{2} + 7 x + 15}$

$\frac{2}{x^{2} - 2 x - 3}$

$= \frac{2. (x - 5)}{(x^{2} - 2 x - 3) (x - 5)}$

$= \frac{2 (x - 5)}{x^{3} - 7 x^{2} + 7 x + 15}$

Bài 4.1 Trang 28 SBT Toán 8 Tập 1: Quy đồng mẫu thức ba phân thức

$\frac{x}{x^{2} - 2 x y + y^{2} - z^{2}}$ , $\frac{y}{y^{2} - 2 y z + z^{2} - x^{2}}$ , $\frac{z}{z^{2} - 2 z x + x^{2} - y^{2}}$

Phương pháp giải:

Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải:

Ta có:

+) $x^{2} - 2 x y + y^{2} - z^{2}$ $= {(x - y)}^{2} - z^{2}$ $= (x - y + z) (x - y - z)$

+) $y^{2} - 2 y z + z^{2} - x^{2}$ $= {(y - z)}^{2} - x^{2}$ $= (y - z + x) (y - z - x)$ $= - (x - y + z) (x + y - z)$

+) $z^{2} - 2 x z + x^{2} - y^{2} = {(x - z)}^{2} - y^{2}$ $= (x - z + y) (x - z - y)$ $= (x + y - z) (x - y - z)$

MTC = $(x - y + z) (x + y - z) (x - y - z)$

$\frac{x}{x^{2} - 2 x y + y^{2} - z^{2}}$ $= \frac{x}{(x - y + z) (x - y - z)}$ $= \frac{x (x + y - z)}{(x - y + z) (x + y - z) (x - y - z)}$

$\frac{y}{y^{2} - 2 y z + z^{2} - x^{2}}$ $= \frac{y}{(y - z + x) (y - z - x)}$ $= \frac{- y}{(x - y + z) (x + y - z)}$ $= \frac{- y (x - y - z)}{(x - y + z) (x + y - z) (x - y - z)}$

$\frac{z}{z^{2} - 2 z x + x^{2} - y^{2}}$ $= \frac{z}{(x + y - z) (x - y - z)}$ $= \frac{z (x - y + z)}{(x + y - z) (x - y + z) (x - y - z)}$

Bài 4.2 Trang 28 SBT Toán 8 Tập 1: Cho hai phân thức $\frac{1}{x^{2} + a x - 2}$ , $\frac{2}{x^{2} + 5 x + b}$ . Hãy xác định $a$ và $b$ biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là $x^{3} + 4 x^{2} + x - 6$ . Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là $x^{3} + 4 x^{2} + x - 6$

Phương pháp giải:

* Phép chia hết là phép chia có số dư bằng $0$ .

* Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:

- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.

- Tìm nhân tử phụ của mỗi mẫu thức.

- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.

Lời giải:

Vì phép chia này là phép chia hết nên số dư phải bằng $0$

$\Rightarrow 3 - a (4 - a) = 0$ (1) và $2 - 2 a = 0$ (2)

Từ (2) ta có: $2 - 2 a = a \Rightarrow a = 1$ và $a = 1$ thỏa mãn (1).

Ta có phân thức $\frac{1}{x^{2} + x - 2}$

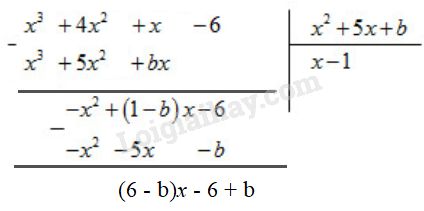
Vì phép chia này là phép chia hết nên số dư phải bằng $0$ .

$\Rightarrow 6 - b = 0$ (3) và $- 6 + b = 0$ (4)

Từ (4) suy ra $b = 6$ và $b = 6$ cũng thỏa mãn (3).

Ta có phân thức $\frac{2}{x^{2} + 5 x + 6}$

Khi đó:

$\begin{aligned} +) \frac{1}{x^{2} + x - 2} \\ = \frac{x + 3}{(x^{2} + x - 2) (x + 3)} \\ = \frac{x + 3}{x^{3} + 4 x^{2} + x - 6} \\ +) \frac{2}{x^{2} + 5 x + 6} \\ = \frac{2 (x - 1)}{(x^{2} + 5 x + 6) (x - 1)} \\ = \frac{2 x - 2}{x^{3} + 4 x^{2} + x - 6} \end{aligned}$