Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 6: Phép trừ các phân thức đại số chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 6: Phép trừ các phân thức đại số
Bài 24 Trang 30 SBT Toán 8 Tập 1: Làm tính trừ phân thức :
a)
b)
c)
d)
e)
f)
g)
h)
Phương pháp giải:
- Áp dụng quy tắc trừ hai phân thức :
- Muốn rút gọn một phân thức đại số ta làm như sau :
+ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung giống nhau.
Lời giải:
a)
b)
c)
d)
e)
f)
g)
h)
Bài 25 Trang 30 SBT Toán 8 Tập 1: Theo định nghĩa của phép trừ, khi viết
có nghĩa là
Áp dụng điều này để làm các phép tính sau :
a)
b)
Phương pháp giải:
Áp dụng quy tắc trừ các phân thức đại số:
có nghĩa là
Từ đó quy đồng mẫu thức rồi đưa về phép cộng các phân thức cùng mẫu.
Lời giải:
a)
b)
Bài 26 Trang 31 SBT Toán 8 Tập 1: Rút gọn biểu thức :
a)
b)
c)
Phương pháp giải:
- Áp dụng quy tắc trừ hai phân thức :
- Muốn rút gọn một phân thức đại số ta làm như sau:
+ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung giống nhau.
Lời giải:
a)
b)
c)
Bài 27 Trang 31 SBT Toán 8 Tập 1: Nếu mua lẻ thì giá một bút bi là đồng. Nhưng nếu mua từ bút trở lên thì giá mỗi bút rẻ hơn đồng. Cô Dung dùng đồng để mua bút cho văn phòng.
Hãy biểu diễn qua :
- Tổng số bút mua được khi mua lẻ ;
- Số bút mua được nếu mua cùng một lúc, biết rằng giá tiền một bút không quá đồng ;
- Số bút được lợi khi mua cùng một lúc so với khi mua lẻ.
Phương pháp giải:
- Số bút mua được khi mua lẻ số tiền cô Dung có giá bút bi khi mua lẻ.
- Số bút mua được khi mua cùng một lúc số tiền cô Dung có giá bút bi khi mua cùng một lúc.
- Số bút được lợi khi mua cùng một lúc so với khi mua lẻ Số bút mua được khi mua cùng một lúc Số bút mua được khi mua lẻ.
Lời giải:
Số bút mua được khi mua lẻ là : (bút)
Vì giá mỗi cây bút không quá đồng nên nếu mua cùng lúc thì số bút lớn hơn Giá mỗi cây bút khi đó là: (đồng) và mua được là (bút)
Số bút được lợi so với mua lẻ là : (bút)
Bài 28 Trang 31 SBT Toán 8 Tập 1: a) Chứng minh
b) Đố. Đố em tính nhẩm được tổng sau :
1
Phương pháp giải:
a) Áp dụng quy tắc trừ hai phân thức :
b) Dựa vào kết quả câu a) để phân tích mỗi phân thức thành một hiệu hai phân thức thích hợp.
Lời giải:
a) Biến đổi vế trái :
Vế trái bằng vế phải, đẳng thức được chứng minh.
b)
Bài 6.1 Trang 31 SBT Toán 8 Tập 1: Thực hiện phép trừ
. Cách thực hiện nào sau đây là sai ?
A.
B.
C.
D.
Phương pháp giải:
Áp dụng quy tắc đưa vào trong dấu ngoặc và sử dụng:
+) Biểu thức chỉ có phép trừ thì thực hiện từ trái sang phải :
+)
+)
Lời giải:
Ta có:
Nên trong các cách thực hiện đã cho, cách thực hiện sai là :
Chọn B.
Bài 6.2 Trang 32 SBT Toán 8 Tập 1: Trong mỗi trường hợp sau hãy tìm phân thức Q thỏa mãn điều kiện :
a)
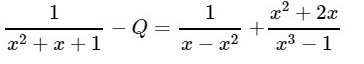
b)
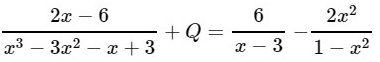
Phương pháp giải:
Áp dụng quy tắc chuyển vế : Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.
Sau đó quy đồng các mẫu thức và cộng trừ các phân thức thu được.
Lời giải:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.