Với giải SGK Toán 8 Cánh Diều trang 18 chi tiết trong Bài 3: Hằng đẳng thức đáng nhớ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải Toán 8 trang 18 Tập 1 (Cánh Diều)
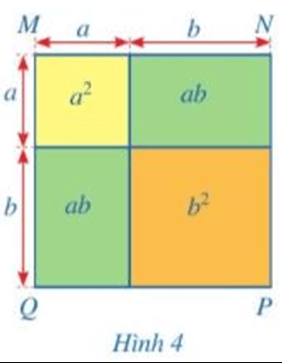
Lời giải:
Ta đặt tên các điểm A, B, C, D như hình vẽ:
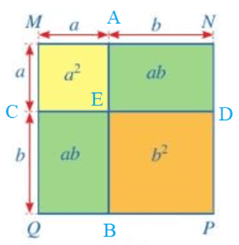
Diện tích của hình vuông MNPQ có thể được tính theo những cách sau:
Cách 1. Tính theo tổng diện tích của 4 hình AMCE, ANDE, BEDP, BECQ.
Cách 2. Tính theo tổng diện tích của 2 hình: MNDC, CDPQ.
Cách 3. Tính theo tổng diện tích của 2 hình: ABQM, ABPN.
Cách 4. Tìm độ dài một cạnh của hình vuông MNPQ rồi tính diện tích.
a) Tại x = 1; y = −1;
b) Tại x = 2; y = −3.
Lời giải:
a) Thay x = 1; y = −1 vào biểu thức P và Q, ta được:
• P = 2 . [1 + (−1)] = 2 . 0 = 0;
• Q = 2 . 1 + 2 . (−1) = 2 – 2 = 0.
Vậy tại x = 1; y = −1 thì P = Q.
b) Thay x = 2; y = −3 vào biểu thức P và Q, ta được:
• P = 2 . [2 + (−3)] = 2 . (−1) = −2;
• Q = 2 . 2 + 2 . (−3) = 4 – 6 = −2.
Vậy tại x = 2; y = −3 thì P = Q.
Luyện tập 1 trang 18 Toán 8 Tập 1: Chứng minh rằng: x(xy2 + y) – y(x2y + x) = 0.
Lời giải:
Ta có x(xy2 + y) – y(x2y + x) = x . xy2 + x . y – y . x2y – y . x
= x2y2 + xy – x2y2 – xy = (x2y2 – x2y2) + (xy – xy) = 0 + 0 = 0 (đpcm)
Hoạt động 2 trang 18 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính:
a) (a + b)(a + b);
b) (a – b)(a – b).
Lời giải:
a) (a + b)(a + b) = a . a + a . b + b . a + b . b = a2 + 2ab + b2;
b) (a – b)(a – b) = a . a – a . b – b . a + b . b = a2 – 2ab + b2.
Xem thêm các bài giải Toán 8 Cánh Diều hay, chi tiết khác:
Luyện tập 1 trang 18 Toán 8 Tập 1: Chứng minh rằng: x(xy2 + y) – y(x2y + x) = 0.
Hoạt động 2 trang 18 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính
Luyện tập 2 trang 19 Toán 8 Tập 1: Tính: a) ; b) (2x + y)2;
Luyện tập 4 trang 19 Toán 8 Tập 1: Tính nhanh: 492.
Luyện tập 5 trang 20 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích
Luyện tập 6 trang 20 Toán 8 Tập 1: Tính: a) (a – 3b)(a + 3b); b) (2x + 5)(2x – 5);
Luyện tập 7 trang 20 Toán 8 Tập 1: Tính nhanh: 48 . 52.
Hoạt động 4 trang 20 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính
Luyện tập 8 trang 21 Toán 8 Tập 1: Tính:a) (3 + x)3; b) (a + 2b)3;
Luyện tập 10 trang 21 Toán 8 Tập 1: Tính nhanh: 1013 – 3 . 1012 + 3 . 101 – 1.
Hoạt động 5 trang 21 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính
Luyện tập 11 trang 22 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích:a) 27x3 + 1; b) 64 – 8y3.
Bài 1 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu
Bài 2 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu
Bài 3 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích:a) 25x2 – 16; b) 16a2 – 9b2;
Bài 6 trang 23 Toán 8 Tập 1: Tính nhanh: (0,76)3 + (0,24)3 + 3 . 0,76 . 024.
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:
Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến
Bài 2: Các phép tính với đa thức nhiều biến
Bài 4: Luyện tập hằng đẳng thức vào phân tích đa thức thành nhân tử
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.