Giải Toán 8 trang 49 Tập 1 (Cánh Diều)

Ngọc Nguyễn Ngày: 23-02-2024 Lớp 8

330

Với giải SGK Toán 8 Cánh Diều trang 49 chi tiết trong Bài tập cuối chương 2 trang 49 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 trang 49 Tập 1 (Cánh Diều)

Bài 1 trang 49 Toán 8 Tập 1: Thực hiện phép tính:

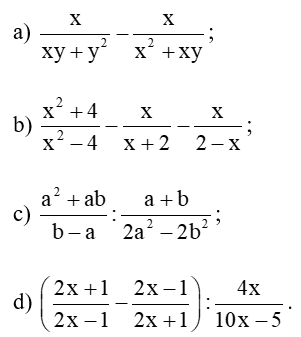
Toán 8 (Cánh diều) Bài tập cuối chương 2 trang 49 (ảnh 1)

Lời giải:

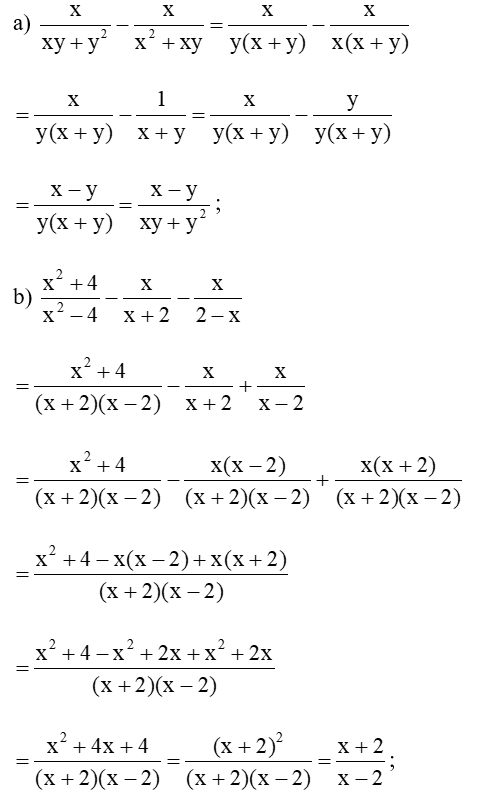
Toán 8 (Cánh diều) Bài tập cuối chương 2 trang 49 (ảnh 2)

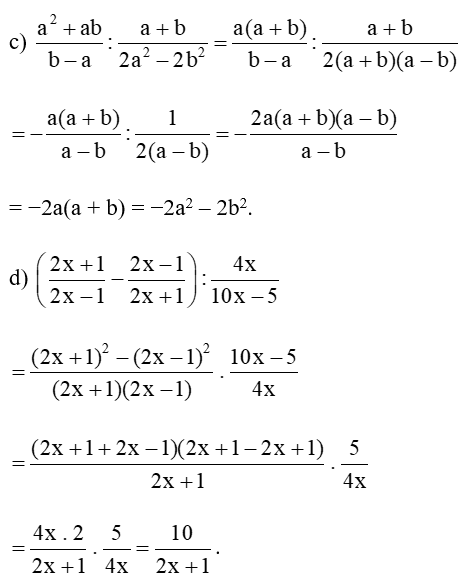
Toán 8 (Cánh diều) Bài tập cuối chương 2 trang 49 (ảnh 4)

Bài 2 trang 49 Toán 8 Tập 1: Cho biểu thức: $A = (\frac{x + 1}{2 x - 2} + \frac{3}{x^{2} - 1} - \frac{x + 3}{2 x + 2}) . \frac{4 x^{2} - 4}{5}$ .

a) Viết điều kiện xác định của biểu thức A;

b) Chứng minh giá trị của biểu thức A không phụ thuộc vào giá trị của biến.

Lời giải:

a) Điều kiện xác định của biểu thức A là:

2x – 2 ≠ 0; x² – 1 ≠ 0; 2x + 2 ≠ 0.

b) Ta có $A = (\frac{x + 1}{2 x - 2} + \frac{3}{x^{2} - 1} - \frac{x + 3}{2 x + 2}) . \frac{4 x^{2} - 4}{5}$

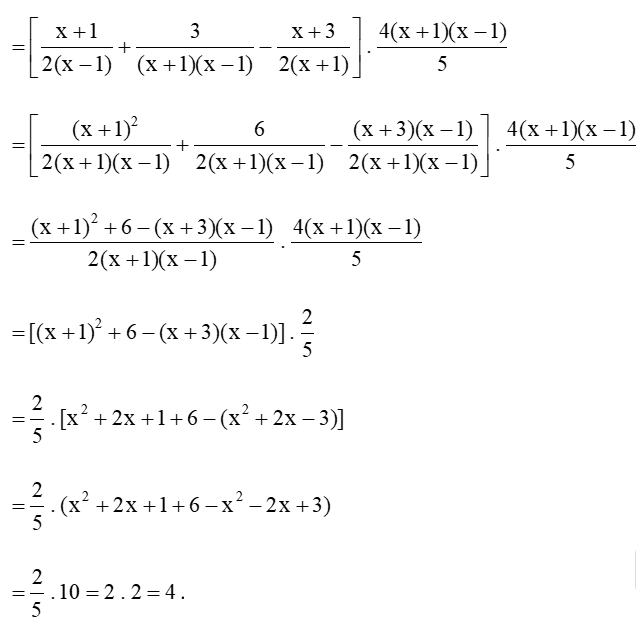
Toán 8 (Cánh diều) Bài tập cuối chương 2 trang 49 (ảnh 5)

Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của biến.

Bài 3 trang 49 Toán 8 Tập 1: Cho biểu thức: $B = (\frac{5 x + 2}{x^{2} - 10 x} + \frac{5 x - 2}{x^{2} + 10 x}) . \frac{x^{2} - 100}{x^{2} + 4}$ .

a) Viết điều kiện xác định của biểu thức B.

b) Rút gọn B và tính giá trị của biểu thức B tại x = 0,1.

c) Tìm số nguyên x để biểu thức B nhận giá trị nguyên.

Lời giải:

a) Điều kiện xác định của biểu thức B là:

x² – 10x ≠ 0; x² + 10x ≠ 0; x² + 4 ≠ 0.

Hay x(x – 10) ≠ 0; x(x + 10) ≠ 0 (vì x² + 4 > 0).

Do đó x ≠ 0; x ≠ ±10.

b) Rút gọn biểu thức B, ta được:

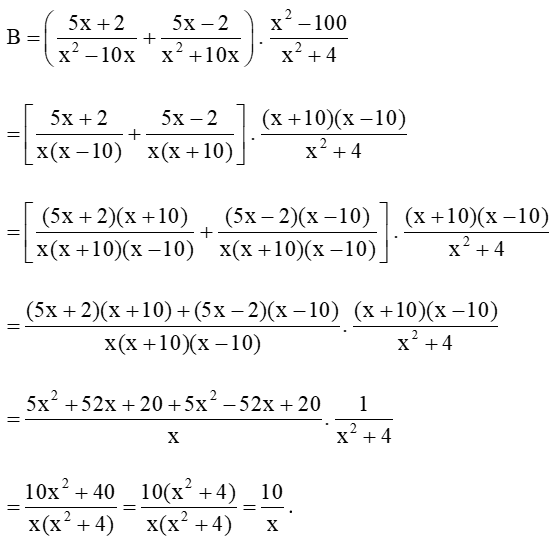
Toán 8 (Cánh diều) Bài tập cuối chương 2 trang 49 (ảnh 6)

Với x = 0,1 (thỏa mãn điều kiện). Khi đó, giá trị của biểu thức B tại x = 0,1 là:

$\frac{10}{x} = \frac{10}{0, 1} = 100$ .

c) Để biểu thức B nhận giá trị nguyên thì 10 ⋮ x hay x ∈ Ư(10) = {±1; ±2; ±5; ±10}.

Mà theo điều kiện xác định: x ≠ 0; x ≠ ±10.

Do đó x ∈ {±1; ±2; ±5}.

Vậy để biểu thức B nhận giá trị nguyên thì x ∈ {±1; ±2; ±5}.

Bài 4 trang 49 Toán 8 Tập 1: Hai người thợ cùng sơn một bức tường. Nếu một mình sơn xong bức tường thì người thứ nhất làm xong lâu hơn người thứ hai là 2 giờ. Gọi x là số giờ mà người thứ nhất một mình sơn xong bức tường. Viết phân thức biểu thị tổng số phần bức tường sơn được mà người thứ nhất sơn trong 3 giờ và người thứ hai sơn trong 4 giờ theo x.

Lời giải:

• Người thứ nhất một mình sơn xong bức tường trong x giờ.

Khi đó, trong 1 giờ người thứ nhất sơn được $\frac{1}{x}$ bức tường.

Do đó, phân thức biểu thị tổng số phần bức tường sơn được mà người thứ nhất sơn trong 3 giờ là $\frac{3}{x}$ bức tường.

• Người thứ nhất làm xong lâu hơn người thứ hai là 2 giờ.

Khi đó, người thứ hai một mình sơn xong bức tường trong x – 2 (giờ).

Khi đó, trong 1 giờ người thứ hai sơn được $\frac{1}{x - 2}$ bức tường.

Do đó, phân thức biểu thị tổng số phần bức tường sơn được mà người thứ hai sơn trong 4 giờ là $\frac{4}{x - 2}$ bức tường.

Bài 5 trang 49 Toán 8 Tập 1: Số tiền hằng năm A (triệu đô la Mỹ) mà người Mỹ chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà và dân số P (triệu người) hằng năm của Mỹ từ năm 2000 đến năm 2006 lần lượt được cho bởi công thức sau: $A = \frac{- 8 242, 58 t + 348 299, 6}{- 0, 06 t + 1}$ với 0 ≤ t ≤ 6; P = 2,71t + 282,7 với 0 ≤ t ≤ 6. Trong đó, t là số năm tính từ năm 2000, t = 0 tương ứng với năm 2000.

(Nguồn: U.S. Bureau of Economic Analysis and U.S. Census Bureau)

Viết phân thức biểu thị (theo t) số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà.

Lời giải:

Phân thức biểu thị (theo t) số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà là:

$\frac{A}{P} = \frac{- 8 242, 58 t + 348 299, 6}{(- 0, 06 t + 1) (2, 71 t + 282, 7)}$ .

Xem thêm các bài giải Toán 8 Cánh Diều hay, chi tiết khác:

Bài 1 trang 49 Toán 8 Tập 1: Thực hiện phép tính x/xy+y^2 - x/x^2+xy

Bài 2 trang 49 Toán 8 Tập 1:Cho biểu thức: $A = (\frac{x + 1}{2 x - 2} + \frac{3}{x^{2} - 1} - \frac{x + 3}{2 x + 2}) . \frac{4 x^{2} - 4}{5}$ . a) Viết điều kiện xác định của biểu thức A;

Bài 3 trang 49 Toán 8 Tập 1:Cho biểu thức: $B = (\frac{5 x + 2}{x^{2} - 10 x} + \frac{5 x - 2}{x^{2} + 10 x}) . \frac{x^{2} - 100}{x^{2} + 4}$ . a) Viết điều kiện xác định của biểu thức B.

Bài 4 trang 49 Toán 8 Tập 1: Hai người thợ cùng sơn một bức tường. Nếu một mình sơn xong bức tường thì người thứ nhất làm xong lâu hơn người thứ hai là 2 giờ.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số

Chủ đề 1: Quản lí tài chính cá nhân

Bài 1: Hàm số

Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

206

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

219