Toptailieu.vn biên soạn và giới thiệu lời giải Bài 2: Hai đường thẳng song song trong không gian hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài 2 từ đó học tốt môn Toán 11.

Toán 11 (Cánh diều) Bài 2: Hai đường thẳng song song trong không gian

Giải Toán 11 trang 95 Tập 1

Câu hỏi khởi động trang 95 Toán 11 Tập 1: Trong thực tế, ta quan sát thấy nhiều hình ảnh gợi nên những đường thẳng song song với nhau. Chẳng hạn các cột treo cờ của tổ chức các nước thành viên ASEAN (Hình 30).

Hai đường thẳng song song trong không gian có tính chất gì?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Hai đường thẳng song song trong không gian là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.

I. Vị trí tương đối của hai đường thẳng phân biệt

Hoạt động 1 trang 95 Toán 11 Tập 1: a) Hãy nêu các vị trí tương đối của hai đường thẳng trong mặt phẳng.

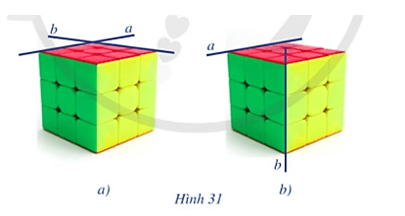
b) Quan sát hai đường thẳng a và b trong Hình 31a, 31b và cho biết các đường thẳng cùng nằm trong một mặt phẳng không.

Lời giải:

a) Trong một mặt phẳng, ta có các vị trí tương đối sau của hai đường thẳng:

– Hai đường thẳng cắt nhau;

– Hai đường thẳng song song với nhau;

– Hai đường thẳng trùng nhau.

b) Hai đường thẳng a và b trong Hình 31a) đang nằm trên cùng một mặt phẳng và cắt nhau.

Hai đường thẳng a và b trong Hình 31b) không cùng nằm trên một mặt phẳng.

Giải Toán 11 trang 97 Tập 1

Luyện tập 1 trang 97 Toán 11 Tập 1: Quan sát một phần căn phòng (Hình 35), hãy cho biết vị trí tương đối của các cặp đường thẳng a và b; a và c; b và c.

Lời giải:

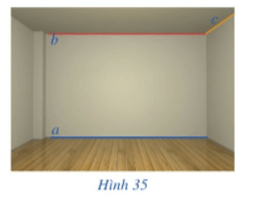
– Hai đường thẳng a và b cùng nằm trong một mặt phẳng là tường nhà và hai đường thẳng này song song với nhau.

– Hai đường thẳng a và c không cùng nằm trên một mặt phẳng do đó hai đường thẳng này chéo nhau.

– Hai đường thẳng b và c cùng nằm trên một mặt phẳng trần nhà và hai đường thẳng này cắt nhau.

II. Tính chất

Hoạt động 2 trang 97 Toán 11 Tập 1: Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.

Lời giải:

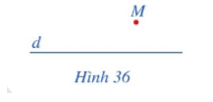
Dự đoán: Trong không gian, qua điểm M ta vẽ được một đường thẳng duy nhất song song với đường thẳng d.

Hoạt động 3 trang 97 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q).

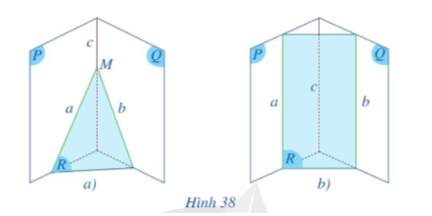
– Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?

– Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?

Lời giải:

– Ta có: a ∩ b = {M}

Mà a ⊂ (P); b ⊂ (Q)

Nên M ∈ (P) và M ∈ (Q)

Do đó M là giao điểm của (P) và (Q).

Mà (P) ∩ (Q) = c, suy ra M ∈ c.

Vậy đường thằng c đi qua điểm M.

– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.

Khi đó N ∈ a  mà a ⊂ (R) nên N ∈ (R)

            N ∈ c mà c ⊂ (Q) nên N ∈ (Q)

Do đó N là giao điểm của (R) và (Q).

Mà (Q) ∩ (R) = b

Suy ra N ∈ b.

Vì thế a và b có điểm chung là N (mâu thuẫn với giả thiết a và b song song).

Vậy nếu đường thẳng a song song với đường thẳng b thì đường thẳng a và b song song với đường thẳng c.

Giải Toán 11 trang 99 Tập 1

Luyện tập 2 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).

Lời giải:

• Ta có: S ∈ (SAB) và S ∈ (SCD) nên S là giao điểm của (SAB) và (SCD).

Mà AB // CD;

      AB ⊂ (SAB);

      CD ⊂ (SCD).

Do đó giao tuyến của (SAB) và (SCD) là đường thẳng n đi qua S và song song với AB và CD.

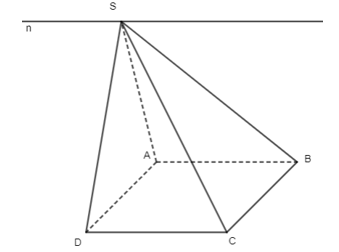
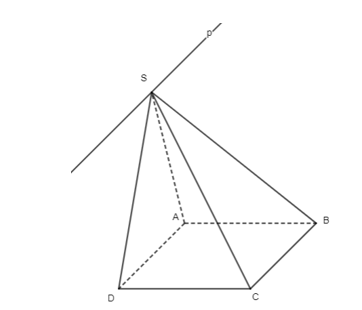
• Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).

Mà AD // BC

      AD ⊂ (SAD);

      BC ⊂ (SBC).

Do đó giao tuyến của (SAD) và (SBC) là đường thẳng p đi qua S và song song với AD và BC.

Hoạt động 4 trang 99 Toán 11 Tập 1: Trong mặt phẳng, hãy nêu vị trí tương đối của hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba.

Lời giải:

Trong mặt phẳng, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.

Giải Toán 11 trang 100 Tập 1

Luyện tập 3 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, SC. Lấy các điểm P, Q lần lượt thuộc các đoạn thẳng AB, BC sao cho $\frac{BP}{BA}=\frac{BQ}{BC}=\frac{1}{3}$ . Chứng minh rằng MN song song với PQ.

Lời giải:

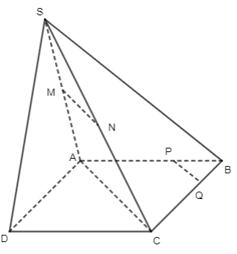
+) Xét tam giác SAC, có:

M là trung điểm SA, N là trung điểm của SC

Do đó MN là đường trung bình của tam giác SAC.

Suy ra MN // AC (1)

+) Xét tam giác ABC, có $\frac{BP}{BA}=\frac{BQ}{BC}=\frac{1}{3}$:

Suy ra PQ // AC (định lí Thalès đảo) (2)

Từ (1) và (2) suy ra MN // PQ.

Bài tập

Bài 1 trang 100 Toán 11 Tập 1: Quan sát phòng học của lớp và nêu lên hình ảnh của hai đường thẳng song song, cắt nhau và chéo nhau.

Lời giải:

Gợi ý những hình ảnh hai đường thẳng song song: Hai rìa mép thước thẳng, hai đường viền bàn đối nhau, đường viền chân tường và đường viền trần nhà (trong cùng một bức tường), hai đường viền bảng đối nhau, ...

Gợi ý những hình ảnh về hai đường thẳng cắt nhau: Hai rìa mép thước kề nhau, hai đường viền bảng kề nhau, đường góc tường và đường chân tường (trong cùng một bức tường), ...

Gợi ý những hình ảnh về hai đường thẳng chéo nhau: Đường chéo của bàn học với đường góc tường, đường chéo của bảng và đường viền chân tường trong bức tường kề với bức tường chứa bảng, ...

Bài 2 trang 100 Toán 11 Tập 1: Quan sát Hình 43 và cho biết vị trí tương đối của hai trong ba cột tuabin gió có trong hình.

Lời giải:

Vị trí tương đối của hai trong ba cột tuabin có trong hình là hai đường thẳng song song.

Bài 3 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD).

Lời giải:

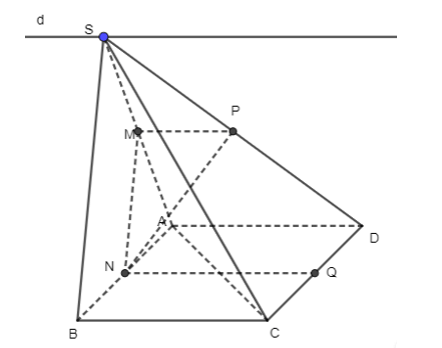
+) Ta có: ABCD là hình bình hành nên AD // BC

Mà AB ⊂ (SAB);

      BC ⊂ (SBC);

      S ∈ (SAB) và S ∈ (SBC).

Vì vậy giao tuyến của hai mặt phẳng là đườ2ng thẳng d đi qua S và song song với AD và BC.

Vậy (SAB) ∩ (SBC) = d.

+) Trong tam giác SAD, có: M, P lần lượt là trung điểm của SA, SD

Do đó MP là đường trung bình nên MP // AD.

Mà MP ⊂ (MNP);

      AD ⊂ (ABCD);

      N ∈ (MNP) và N ∈ (ABCD).

Vì vậy giao tuyến của hai mặt phẳng là đường thẳng đi qua N và song song với AD và BC, cắt CD tại Q.

Vậy (MNP) ∩ (ABCD) = NQ.

Bài 4 trang 100 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G₁, G₂ lần lượt là trọng tâm của các tam giác ABC, ABD. Chứng minh rằng đường thẳng G₁G₂ song song với đường thẳng CD.

Lời giải:

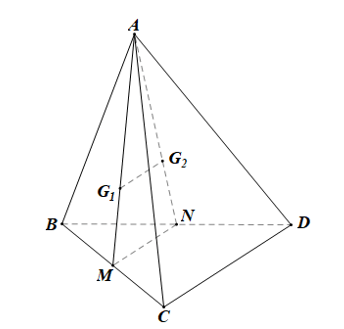
+) Trong mặt phẳng ABC, kẻ đường trung tuyến AM (M ∈ BC).

Do G₁ là trọng tâm của tam giác ABC nên $\frac{A{G}_1}{AM}=\frac{2}{3}$ .

+) Trong mặt phẳng ABD, kẻ đường trung tuyến AN (N ∈ BD).

Do G₂ là trọng tâm của tam giác ABD nen $\frac{A{G}_2}{AN}=\frac{2}{3}$ .

+) Xét tam giác AMN, có $\frac{A{G}_1}{AM}=\frac{A{G}_2}{AN}=\frac{2}{3}$ nên G₁G₂ // MN (định lí Thalès đảo).

+) Xét tam giác BCD, có: M, N lần lượt là trung điểm của BC, BD

Do đó MN là đường trung bình của tam giác BCD.

Suy ra MN // CD.

Mà G₁G₂ // MN (chứng minh trên) nên G₁G₂ // CD.

Bài 5 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.

Lời giải:

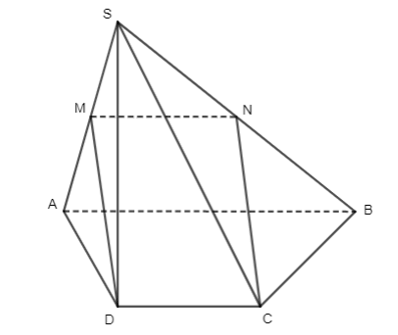
Trong mặt phẳng (SAB), có: M, N lần lượt là trung điểm của SA và SB

Do đó MN là đường trung bình của tam giác

Suy ra MN // AB và MN = $\frac{1}{2}$ AB.

Lại có AB // CD (do ABCD là hình thang) và AB = 2CD hay CD = $\frac{1}{2}$ AB

Do đó MN // CD và MN = CD.

Suy ra MNCD là hình bình hành.

Vì vậy MD // NC.

Bài 6 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.

a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.

 b) Chứng minh rằng IK // BC.

c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC).

Lời giải:

a)

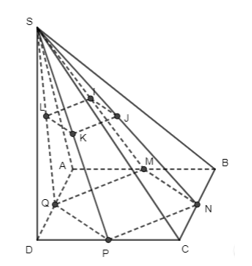
Trong tam giác SMN, có: IJ // MN (tính chất đường trung bình) và IJ = $\frac{1}{2}$ MN.

Trong tam giác SQP, có: LK // QP (tính chất đường trung bình) và LK = $\frac{1}{2}$ PQ.

Mà QP // AC // MN (tính chất đường trung bình) và PQ = MN = $\frac{1}{2}$ AC

Do đó IJ // LK  và IJ = LK

Vậy qua hai đường thẳng song song ta xác định được duy nhất một mặt phẳng chứa hai đường thẳng song song đó hay I, J, K, L đồng phẳng.

Xét tứ giác IJKL có IJ // LK và IJ = LK nên IJKL là hình bình hành.

b)

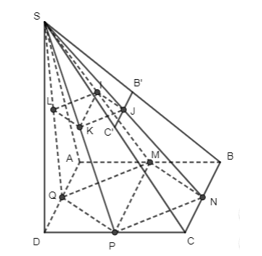
Trong tam giác SMP có: IK // MP (tính chất đường trung bình tam giác SMP)

Mà MP // AD // BC (tính chất đường trung bình của hình thang)

Suy ra IK // BC.

c) Ta có: J ∈ SN mà SN ⊂ (SBC) nên J ∈ (SBC)

Lại có J ∈ (IJKL)

Do đó J là giao điểm của (IJKL) và (SBC).

Mặt khác: IK // BC (chứng minh trên);

                 IK ⊂ (IJKL);

                 BC ⊂ (SBC).

Do đó giao tuyến của hai mặt phẳng (IJKL) và (SBC) là đường thẳng đi qua J song song với BC cắt SB, SC lần lượt tại B’ và C’.

Vậy (IJKL) ∩ (SBC) = B’C’.

Bài 7 trang 100 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.

Lời giải:

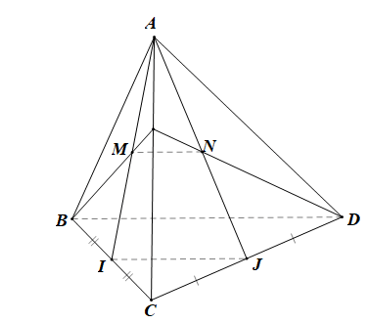
• Ta có: B ∈ (BDK) và B ∈ (BCD) nên B là giao điểm của (BDK) và (BCD).

             D ∈ (BDK) và D ∈ (BCD) nên D là giao điểm của (BDK) và (BCD).

Do đó (BDK) ∩ (BCD) = BD.

• Ta có: M ∈ BK mà BK ⊂ (BDK) nên M ∈ (BDK); 

             M ∈ AI mà AI ⊂ (AIJ) nên M ∈ (AIIJ)

Do đó M là giao điểm của (BDK) và (AIJ)

Tương tự ta cũng có N là giao điểm của (BDK) và (AIJ)

Suy ra (BDK) ∩ (AIJ) = MN.

• Ta có: I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD)

Lại có I ∈ (AIJ) nên I là giao điểm của (BCD) và (AIJ)

Tương tự ta cũng có J là giao điểm của (BCD) và (AIJ)

Suy ra (BCD) ∩ (AIJ) = IJ.

• Xét DBCD có I, J lần lượt là trung điểm của BC, CD nên IJ là đường trung bình của tam giác

Do đó IJ // BD.

• Ta có: (BDK) ∩ (BCD) = BD;

             (BDK) ∩ (AIJ) = MN;

             (BCD) ∩ (AIJ) = IJ;

             IJ // BD.

Suy ra MN // BD.

Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Hình lăng trụ và hình hộp