Với giải SGK Toán 11 Kết nối tri thức trang 56 chi tiết trong Bài tập cuối chương 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 56 Tập 1 (Kết nối tri thức)

Bài 2.22 trang 56 Toán 11 Tập 1: Khẳng định nào sau đây là sai?

A. Một dãy số tăng thì bị chặn dưới.

B. Một dãy số giảm thì bị chặn trên.

C. Một dãy số bị chặn thì phải tăng hoặc giảm.

D. Một dãy số không đổi thì bị chặn.

Lời giải:

Đáp án đúng là: C

+) Mỗi dãy số tăng đều bị chặn dưới bởi số hạng đầu u₁ vì u₁ < u₂ < u₃ < ...., do đó đáp án A đúng.

+) Mỗi dãy số giảm đều bị chặn trên bởi số hạng đầu u₁ vì u₁ > u₂ > u₃ > ...., do đó đáp án B đúng.

+) Một dãy số bị chặn không nhất thiết phải là dãy số tăng hoặc giảm. Chẳng hạn ta xét dãy số (u_n) có số hạng tổng quát u_n = ${\left(-1\right)}^{n-1}\sin \frac{1}{n}$ .

Ta có nhận xét rằng dãy số này đan dấu nên nó không tăng, không giảm.

Mặt khác ta có: 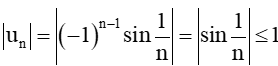 , suy ra dãy số (u_n) bị chặn.

Vậy đáp án C sai.

+) Đáp án D đúng do dãy số (u_n) không đổi thì mọi số hạng luôn bằng nhau và luôn tồn tại m, M để m ≤ u_n ≤ M với mọi n ∈ ℕ^*.

Bài 2.23 trang 56 Toán 11 Tập 1: Cho dãy số

1, $\frac{1}{2},\frac{1}{4},\frac{1}{8},\mathrm{...}$ (số hạng sau bằng một nửa số hạng liền trước nó).

Công thức tổng quát của dãy số đã cho là

A. $u_n={\left(\frac{1}{2}\right)}^n$ .

B. $u_n=\frac{{\left(-1\right)}^n}{2^{n-1}}$ .

C. $u_n=\frac{1}{2n}$ .

D. $u_n={\left(\frac{1}{2}\right)}^{n-1}$ .

Lời giải:

Đáp án đúng là: D

Xét từng đáp án, ta thấy:

+) Đáp án A, dãy số có số hạng tổng quát là $u_n={\left(\frac{1}{2}\right)}^n$ có số hạng đầu $u_1={\left(\frac{1}{2}\right)}^1=\frac{1}{2}$, không thỏa mãn.

+) Đáp án B, dãy số có số hạng tổng quát là $u_n=\frac{{\left(-1\right)}^n}{2^{n-1}}$ có số hạng đầu $u_1=\frac{{\left(-1\right)}^1}{2^{1-1}}=-1$, không thỏa mãn.

+) Đáp án C, dãy số có số hạng tổng quát là $u_n=\frac{1}{2n}$ có số hạng đầu $u_1=\frac{1}{2.1}=\frac{1}{2}$, không thỏa mãn.

+) Đáp án D, dãy số có số hạng tổng quát là $u_n={\left(\frac{1}{2}\right)}^{n-1}$ có số hạng đầu $u_1={\left(\frac{1}{2}\right)}^{1-1}=1$, thỏa mãn.

Bài 2.24 trang 56 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = 3n + 6. Khẳng định nào sau đây là đúng?

A. Dãy số (u_n) là cấp số cộng với công sai d = 3.

B. Dãy số (u_n) là cấp số cộng với công sai d = 6.

C. Dãy số (u_n) là cấp số nhân với công bội q = 3.

D. Dãy số (u_n) là cấp số nhân với công bội q = 6.

Lời giải:

Đáp án đúng là: A

Ta có: u_n – u_{n – 1} = (3n + 6) – [3(n – 1) + 6] = 3n + 6 – (3n – 3 + 6) = 3, với mọi n ≥ 2.

Do đó, (u_n) là cấp số cộng có công sai d = 3.

Bài 2.25 trang 56 Toán 11 Tập 1: Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?

A. u₁ = – 1, $u_{n+1}=u_n^2$.

B. u₁ = – 1, u_{n + 1} = 2u_n.

C. u₁ = – 1, u_{n + 1} = u_n + 2.

D. u₁ = – 1, u_{n + 1} = u­_n – 2.

Lời giải:

Đáp án đúng là: B

Nhận xét thấy dãy số cho bởi công thức truy hồi u₁ = – 1, u_{n + 1} = 2u_n có $\frac{u_{n+1}}{u_n}=2$ với mọi n ≥ 1. Do đó, dãy số này là một cấp số nhân với số hạng đầu u₁ = – 1 và công bội q = 2.

Bài 2.26 trang 56 Toán 11 Tập 1: Tổng 100 số hạng đầu của dãy số (u_n) với u_­n = 2n – 1 là

A. 199.

B. 2¹⁰⁰ – 1.

C. 10 000.

D. 9 999.

Lời giải:

Đáp án đúng là: C

Ta có: u_n – u_{n – 1} = (2n – 1) – [2(n – 1) – 1] = 2n – 1 – (2n – 2 – 1) = 2, với mọi n ≥ 2.

Do đó, dãy số (u_n) là một cấp số cộng có u₁ = 2 . 1 – 1 = 1 và công sai d = 2.

Tổng 100 số hạng đầu tiên của cấp số cộng này là

S₁₀₀ = $\frac{100}{2}\left(2u_1+\left(100-1\right)d\right)$ = 50(2 . 1 + 99 . 2) = 10 000.