Toptailieu.vn biên soạn và giới thiệu lời Toán 11 (Kết nối tri thức) Bài 14: Phép chiếu song song hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Sgk Toán 11 Bài 14 từ đó học tốt môn Toán 11.

Toán 11 (Kết nối tri thức) Bài 14: Phép chiếu song song

Giải Toán 11 trang 95

Mở đầu trang 95 Toán 11 Tập 1: Trong bóng đá, công nghệ Goal-line được sử dụng để xác định xem bóng đã hoàn toàn vượt qua vạch vôi hay chưa, từ đó giúp trọng tài đưa ra quyết định về một bàn thắng có được ghi hay không. Yếu tố hình học nào cho ta biết quả bóng đã vượt qua vạch vôi hay chưa?

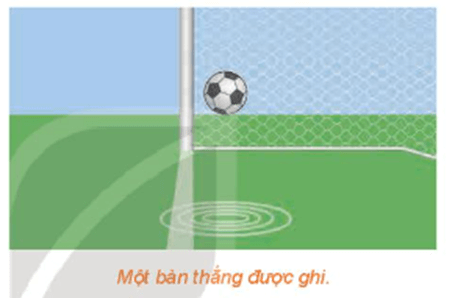
Lời giải:

Sau bài học này ta sẽ giải quyết bài toán trên như sau:

Khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng có vị trí ở phía sau vạch vôi, tức là hình chiếu này nằm trong khung thành. Do đó, yếu tố hình học liên quan đến phép chiếu song song cho ta biết quả bóng đã vượt qua vạch vôi hay chưa.

1. Phép chiếu song song

HĐ1 trang 95 Toán 11 Tập 1: Một khung cửa sổ có dạng hình tròn với các chấn song tạo thành hình vuông ABCD, hai đường chéo của hình vuông cắt nhau tại O. Dưới ánh mặt trời, khung cửa và các chấn song đổ bóng lên sàn nhà (H.4.56a). Quan sát hình vẽ và trả lời các câu hỏi sau:

a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' có đôi một song song hay không?

b) Làm thế nào để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ?

Lời giải:

a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' đôi một song song với nhau.

b) Để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ ta sử dụng phép chiếu song song.

Giải Toán 11 trang 97

Câu hỏi trang 96 Toán 11 Tập 1: Trong HĐ1, làm thế nào để xác định được bóng của toàn bộ song cửa CD trên sàn nhà?

Lời giải:

Để xác định được bóng của toàn bộ song cửa CD, ta xác định bóng của từng điểm C và D trên sàn nhà là C' và D'. Khi đó C'D' chính là bóng của song cửa CD.

Luyện tập 1 trang 97 Toán 11 Tập 1: Cho hình hộp ABCD.EFGH (H.4.58). Xác định hình chiếu của điểm A trên mặt phẳng (CDHG) theo phương BC và theo phương BG.

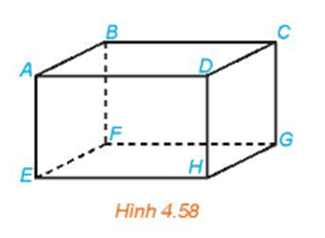
Lời giải:

+) Vì ABCD.EFGH là hình hộp nên AD // BC. Vì D thuộc mặt phẳng (CDHG) nên D là hình chiếu của điểm A trên mặt phẳng (CDHG) theo phương BC.

+) Vì ABCD.EFGH là hình hộp nên các mặt của nó đều là các hình bình hành. Do đó, ABCD và CDHG là các hình bình hành. Từ đó suy ra AB // CD, AB = CD và CD // HG, CD = HG nên AB // HG và AB = HG, suy ra ABGH là hình bình hành nên AH // BG. Vì H thuộc mặt phẳng (CDHG) nên H là hình chiếu của điểm A trên mặt phẳng (CDHG) theo phương BG.

Vận dụng 1 trang 97 Toán 11 Tập 1: Trong hình ảnh mở đầu, khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng có vị trí như thế nào với vạch vôi?

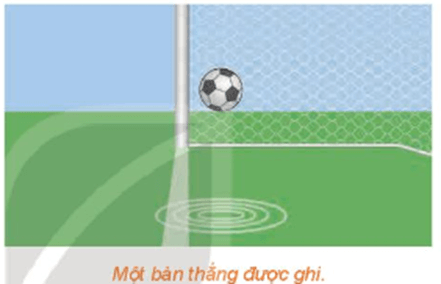
Lời giải:

Trong hình ảnh mở đầu, khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng nằm phía trong vạch vôi về phía bên trong khung thành.

2. Tính chất của phép chiếu song song

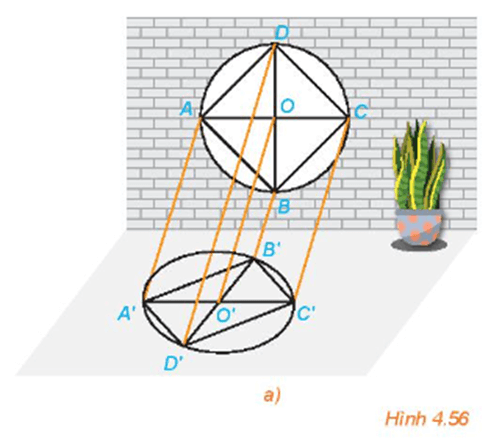
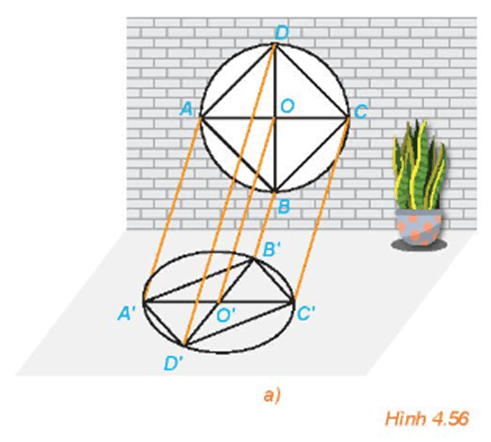
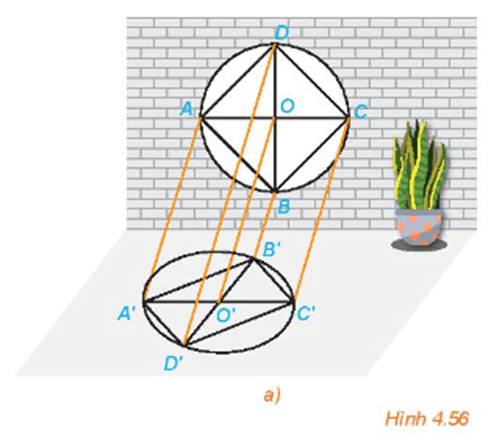
HĐ2 trang 97 Toán 11 Tập 1: Quan sát Hình 4.56a và trả lời các câu hỏi sau:

a) Hình chiếu O' của điểm O có nằm trên đoạn A'C' hay không?

b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau?

c) Hình chiếu O' của điểm O có phải là trung điểm của đoạn A'C' hay không?

Lời giải:

Quan sát Hình 4.56a ta thấy:

a) Hình chiếu O' của điểm O nằm trên đoạn A'C'.

b) Hình chiếu của hai song cửa AB và CD lần lượt là A'B' và C'D', chúng song song với nhau.

c) Hình chiếu O' của điểm O là trung điểm của đoạn A'C'.

Câu hỏi trang 97 Toán 11 Tập 1: Hình chiếu của hai đường thẳng cắt nhau có phải là hai đường thẳng cắt nhau hay không?

Lời giải:

Hình chiếu của hai đường thẳng cắt nhau có thể cắt nhau hoặc trùng nhau.

Giải Toán 11 trang 98

Luyện tập 2 trang 98 Toán 11 Tập 1: Chứng minh rằng hình chiếu song song của một hình thang là một hình thang (H.4.61).

Lời giải:

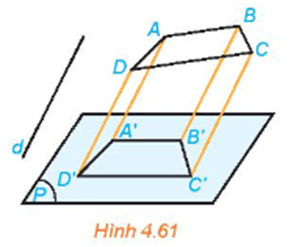
Hình thang ABCD có AB // CD, A'B'C'D' là hình chiếu song song của ABCD trên mặt phẳng (P) theo phương d (Hình 4.61).

Vì ABCD là hình thang có AB // CD, do đó hình chiếu của AB là A'B' song song với hình chiếu của CD là C'D'.

Tứ giác A'B'C'D' có A'B' // C'D' nên nó là hình thang.

Luyện tập 3 trang 98 Toán 11 Tập 1: Một phép chiếu song song biến tam giác ABC thành tam giác A'B'C'. Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC thành đường trung bình của tam giác A'B'C'.

Lời giải:

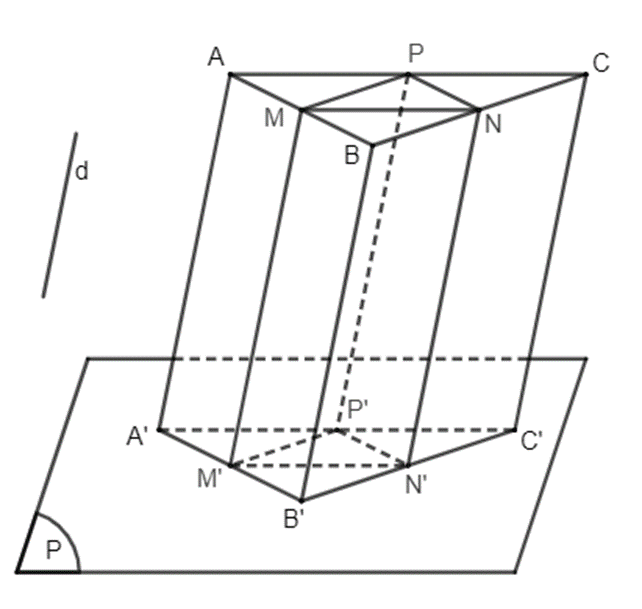
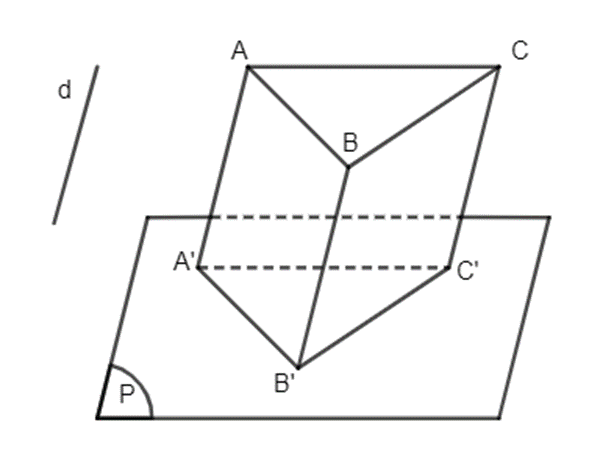
Tam giác A'B'C' là hình chiếu của tam giác ABC trên mặt phẳng (P) theo phương d.

Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Khi đó MN, NP, MP là các đường trung bình của tam giác ABC.

Gọi M', N', P' lần lượt là hình chiếu của M, N, P trên mặt phẳng (P) theo phương d.

Vì M là trung điểm của AB nên A, M, B thẳng hàng theo thứ tự đó và $\frac{AM}{MB}=1$ . Do vậy A', M', B' thẳng hàng theo thứ tự đó và $\frac{A^{\text{'}}{M}^{\text{'}}}{M^{\text{'}}{B}^{\text{'}}}=1$ , tức là M' là trung điểm của A'B'. Chứng minh tương tự ta có N' là trung điểm của B'C' và P' là trung điểm của A'C'. Vậy M'N', N'P', M'P' là các đường trung bình của tam giác A'B'C'.

3. Hình biểu diễn của một hình không gian

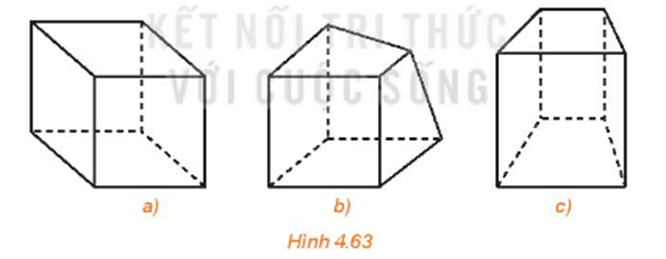
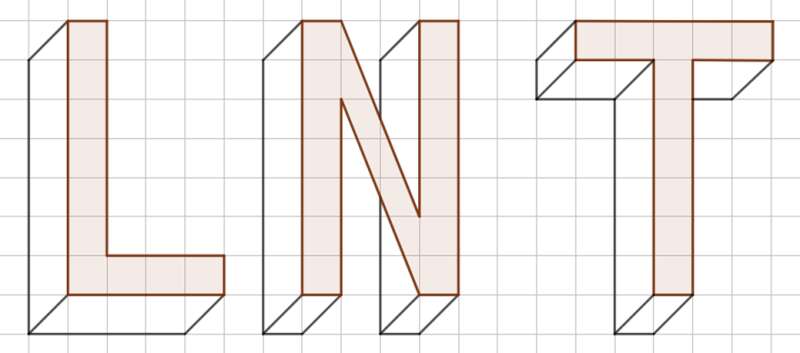
HĐ3 trang 98 Toán 11 Tập 1: Trong ba hình dưới đây, hình nào thể hiện hình lập phương chính xác hơn?

Lời giải:

Trong ba hình đã cho, Hình 4.63a thể hiện hình lập phương chính xác nhất.

Câu hỏi trang 98 Toán 11 Tập 1: Quan sát hình ảnh khung cửa sổ trong Hình 4.56a và cho biết hình biểu diễn của hình tam giác, hình vuông, hình tròn là hình gì?

Lời giải:

Quan sát hình ảnh khung cửa sổ trong Hình 4.56a, ta thấy:

- Hình biểu diễn của hình tam giác là hình tam giác;

- Hình biểu diễn của hình vuông là hình bình hành;

- Hình biểu diễn của hình tròn là hình elip.

Giải Toán 11 trang 99

Luyện tập 4 trang 99 Toán 11 Tập 1: Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình bình hành.

Lời giải:

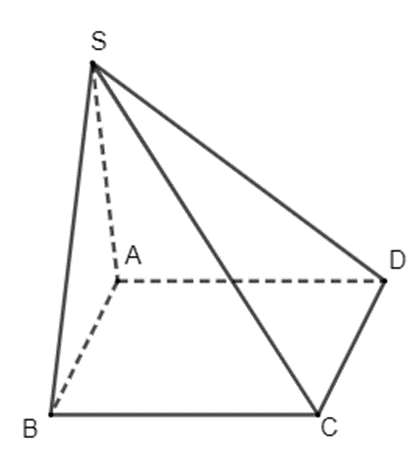
Hình chóp S.ABCD có các mặt bên là các hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác, đáy ABCD là hình bình hành nên hình biểu diễn của đáy ABCD cũng là một hình bình hành. Từ đó ta vẽ được hình biểu diễn của hình chóp S.ABCD như sau:

Vận dụng 2 trang 99 Toán 11 Tập 1: Phép chiếu song song có thể được sử dụng để vẽ dạng nổi (hay dạng 3D) của chữ cái như trong hình dưới đây. Theo phương pháp đó hãy vẽ dạng nổi của một số chữ cái quen thuộc như L, N, T, ...

Lời giải:

Bài tập

Giải Toán 11 trang 100

Bài 4.29 trang 100 Toán 11 Tập 1: Những mệnh đề nào trong các mệnh đề sau đây là đúng?

a) Phép chiếu song song biến đoạn thẳng thành đoạn thẳng.

b) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng cắt nhau.

c) Phép chiếu song song biến tam giác đều thành tam giác cân.

d) Phép chiếu song song biến hình vuông thành hình bình hành.

Lời giải:

a) Mệnh đề a) là mệnh đề đúng.

b) Mệnh đề b) là mệnh đề sai vì phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

c) Mệnh đề c) là mệnh đề sai vì phép chiếu song song biến tam giác đều thành một tam giác bất kì.

d) Mệnh đề d) là mệnh đề đúng.

Bài 4.30 trang 100 Toán 11 Tập 1: Nếu tam giác A'B'C' là hình chiếu của tam giác ABC qua một phép chiếu song song thì tam giác ABC có phải là hình chiếu của tam giác A'B'C' qua một phép chiếu song song hay không? Giải thích vì sao.

Lời giải:

Nếu tam giác A'B'C' là hình chiếu của tam giác ABC qua một phép chiếu song song thì tam giác ABC cũng là hình chiếu của tam giác A'B'C' qua một phép chiếu song song.

Giả sử tam giác A'B'C' là hình chiếu của tam giác ABC trên mặt phẳng (P) theo phương chiếu d. Khi đó AA', BB', CC' đôi một song song với nhau và đều song song với phương chiếu d. Do vậy, tam giác ABC là hình chiếu của tam giác A'B'C' trên mặt phẳng (ABC) theo phương d.

Bài 4.31 trang 100 Toán 11 Tập 1: Phép chiếu song song biến tam giác ABC thành tam giác A'B'C'. Chứng minh rằng phép chiếu đó biến trọng tâm của tam giác ABC thành trọng tâm của tam giác A'B'C'.

Lời giải:

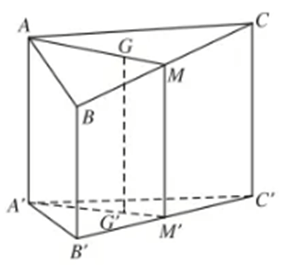
Gọi G là trọng tâm của tam giác ABC và G' là hình chiếu song song của nó. Gọi M là trung điểm của BC thì A, G, M thẳng hàng theo thứ tự đó. Gọi M' là hình chiếu của M. Khi đó, theo tính chất của phép chiếu song song ta có:

A', G', M' thẳng hàng theo thứ tự đó và $\frac{A^{\text{'}}{G}^{\text{'}}}{A^{\text{'}}{M}^{\text{'}}}=\frac{AG}{AM}=\frac{2}{3}$ (1).

B', M', C' thẳng hàng theo thứ tự đó và $\frac{B^{\text{'}}{M}^{\text{'}}}{M^{\text{'}}{C}^{\text{'}}}=\frac{BM}{MB}=1$ (2).

Từ (1) và (2) suy ra G' là trọng tâm của tam giác A'B'C'.

Bài 4.32 trang 100 Toán 11 Tập 1: Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?

Lời giải:

+) Xét hình lục giác đều MNPQRS có tâm O.

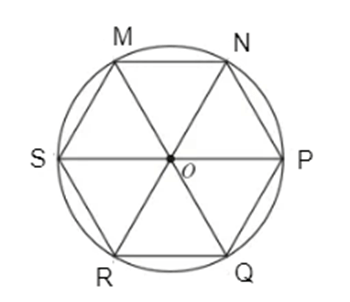
Ta nhận thấy:

- Tứ giác OSMN là hình thoi;

- Các điểm P, Q, R lần lượt là các điểm đối xứng của các điểm S, M, N qua tâm O.

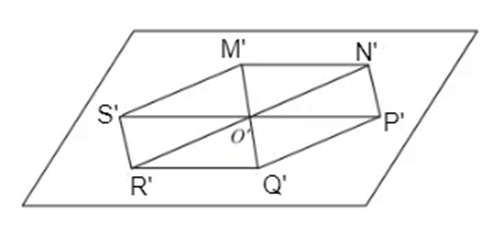
Từ đó suy ra các vẽ hình biểu diễn của hình lục giác đều MNPQRS như sau:

- Vẽ hình bình hành O'S'M'N' biểu diễn cho hình thoi OSMN;

- Lấy các điểm P', Q', R' lần lượt là các điểm đối xứng của các điểm S', M', N' qua O', ta được hình biểu diễn M'N'P'Q'R'S' của hình lục giác đều MNPQRS.

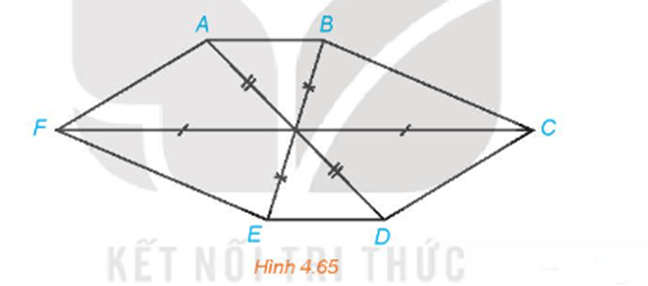
+) Gọi I là giao điểm các đường chéo AD, BE và CF trong hình lục giác ABCDEF ở Hình 4.65.

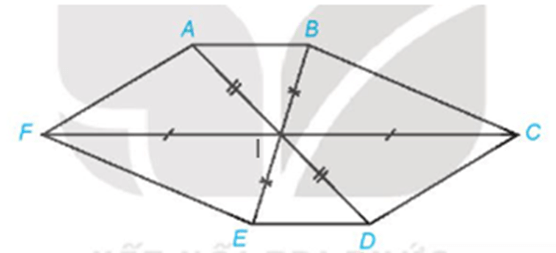
Khi đó nếu ABCDEF là hình biểu diễn của hình lục giác đều thì phải thỏa mãn hai điều kiện:

- Tứ giác IFAB là hình bình hành (1);

- D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua I (2).

Từ hình vẽ ta thấy điều kiện (2) thỏa mãn nhưng điều kiện (1) không thỏa mãn. Vậy Hình 4.65 không thể là hình biểu diễn của một hình lục giác đều.

Bài 4.33 trang 100 Toán 11 Tập 1: Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 2 cm, CD = 6 cm.

Lời giải:

Vì AB = 2 cm, CD = 6 cm nên CD = 3AB.

Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác, đáy ABCD là hình thang có hai đáy AB, CD (do AB // CD) và CD = 3AB nên hình biểu diễn của ABCD là một hình thang có độ dài một đáy gấp ba lần độ dài của đáy còn lại. Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD như sau:

Bài 4.34 trang 100 Toán 11 Tập 1: Trong hình bên, AB và CD là bóng của hai thanh chắn của một chiếc thang dưới ánh mặt trời.

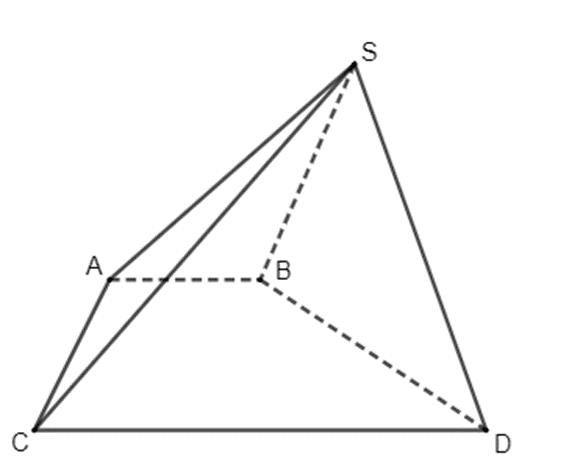
Hãy giải thích tại sao AB song song với CD.

Lời giải:

AB và CD là bóng của hai thanh chắn của một chiếc thang dưới ánh mặt trời. Khi đó AB và CD là hình chiếu song song của hai thanh chắn của một chiếc thang lên tường (do mặt trời chiếu xuống tường các tia sáng song song). Mà hai thanh chắn của một chiếc thang thì song song với nhau, do đó theo tính chất của phép chiếu song song ta suy ra AB song song với CD.

Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số