Với giải SGK Toán 11 Chân trời sáng tạo trang 137 chi tiết trong Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 137 Tập 1 (Chân trời sáng tạo)

Thực hành 1 trang 137 Toán 11 Tập 1: Hãy trả lời câu hỏi ở hoạt động khởi động.

Lời giải:

Ta có bảng tần số ghép nhóm sau:

+) Ước lượng chiều cao trung bình của các vận động viên đội Sao La là:

$\overline{x_1}=\frac{172,5.2+177,5.4+182,5.5+187,5.5+192,5.4}{20}\approx 183,75$ (cm).

Ước lượng chiều cao trung bình của các vận động viên đội Kim Ngưu là:

$\overline{x_2}=\frac{172,5.2+177,5.3+182,5.4+187,5.10+192,5.1}{20}\approx 183,75$ (cm).

Theo chiều cao trung bình thì cả hai đội có chiều cao như nhau.

+) Sau bài này ta sẽ tìm được cách tìm trung vị của mẫu số liệu trên như sau

- Trung vị của dãy số liệu chiều cao đội Sao La là:

Gọi x₁; x₂; x₃; ...; x₂₀ là chiều cao của 20 thành viên đội Sao La xếp theo thứ tự không giảm.

Số trung vị của mẫu số liệu trên là: $\frac{1}{2}$(x₁₀ + x₁₁)

Từ bảng số liệu trên ta thấy x₁; x₂ ∈ [170; 175); x₃; x₄; x₅; x₆ ∈ [175; 180); x₇; x₈; x₉; x₁₀; x₁₁ ∈ [180; 185).

Do đó $\frac{1}{2}$(x₁₀ + x₁₁) sẽ thuộc nhóm [180; 185).

Khi đó số trung vị của số liệu đội Sao La là:

$M_e=180+\frac{\frac{20}{2}-(2+4)}{5}(185-180)=184$.

- Trung vị của dãy số liệu chiều cao đội Kim Ngưu là:

Gọi y₁; y₂; y₃; ...; y₂₀ là chiều cao của 20 thành viên đội Kim Ngưu xếp theo thứ tự không giảm.

Số trung vị của mẫu số liệu trên là: $\frac{1}{2}$(y₁₀ + y₁₁)

Từ bảng số liệu trên ta thấy y₁; y₂ ∈ [170; 175); y₃; y₄; y₅ ∈ [175; 180); y₆; y₇; x₈; x₉ ∈ [180; 185); x₁₀; x₁₁; ...; x₁₉ ∈ [185; 190); x₂₀ ∈ [190; 195).

Do đó $\frac{1}{2}$(x₁₀ + x₁₁) sẽ thuộc nhóm [190; 195).

Khi đó số trung vị của số liệu đội Kim Ngưu là:

$M_e=190+\frac{\frac{20}{2}-(2+3+4)}{10}(195-190)=190,5$.

Dựa vào số trung vị ta thấy chiều cao của đội Kim Ngưu nhỉnh hơn chiều cao của đội Sao La.

Vận dụng 1 trang 137 Toán 11 Tập 1: Trong một hội thao, thời gian chạy 200 m của một nhóm các vận động viên được ghi lại trong bảng sau:

Dựa vào bảng số liệu trên, ban tổ chứ muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây?

Lời giải:

Tổng số vận động viên n = 5 + 12 + 32 + 45 + 30 = 124.

Gọi x₁; x₂; ...; x₁₂₄ lần lượt là thời gian chạy của 124 vận động viên tham gia hội thao được xếp theo thứ tự không giảm.

Ta có: x₁; ...; x₅ ∈ [21; 21,5), x₆; ...; x₁₇ ∈ [21,5; 22), x₁₈; ...; x₄₉ ∈ [22; 22,5), x₅₀; ...; x₉₄ ∈ [22,5; 23), x₉₅; ...; x₁₂₄ ∈ [23; 23,5).

Số trung vị của dãy số liệu là: $\frac{1}{2}$(x₆₂ + x₆₃)

Mà x₆₂; x₆₃ ∈ [22,5; 23) do đó: M_e = $22,5+\frac{\frac{124}{2}-49}{45}(23-22,5)\approx 22,6$.

Vậy ban tổ chức nên chọn vận động viên có thời gian chạy không quá 22,6 giây.

2. Tứ phân vị

Hoạt động khám phá 2 trang 138 Toán 11 Tập 1: Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:

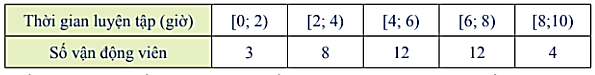
Huấn luyện viên muốn xác định nhóm gồm 25% các vận động viên có số giờ luyện tập cao nhất. Hỏi huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ bao nhiêu giờ trở lên vào nhóm này?

Lời giải:

Số vận động viên được khảo sát là: n = 3 + 8 + 12 + 12 + 4 = 39.

Gọi x₁; x₂; ...; x₃₉ là thời gian luyện tập của 39 vận động viên được xếp theo thứ tự không giảm.

Ta có: x₁; x₂; x₃ ∈ [0; 2), x₄; ...; x₁₁ ∈ [2; 4), x₁₂; ...; x₂₃ ∈ [4; 6), x₂₄; ...; x₃₅ ∈ [6; 8), x₃₆; ...; x₃₉ ∈ [8; 10).

Do đó đối với dãy số liệu x₁; x₂; ...; x₃₉ thì:

- Tứ phân vị thứ nhất là x₁₀ thuộc nhóm [2; 4);

- Tứ phân vị thứ hai là x₂₀ thuộc nhóm [4; 6);

- Tứ phân vị thứ ba là x₃₀ thuộc nhóm [6; 8).

Vậy huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ x₃₀ (giờ) trở lên.