Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 4: Đường trung bình của tam giác, hình thang chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 4: Đường trung bình của tam giác, hình thang
Bài 34 Trang 84 SBT Toán 8 Tập 1 Cho tam giác ABC, điểm D thuộc cạnh AC sao cho . Gọi M là trung điểm của BC, I là giao điểm của và Chứng minh rằng
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
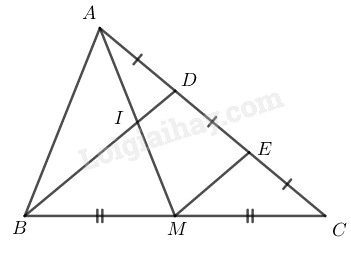
Gọi là trung điểm của
Trong ta có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của
( tính chất đường trung bình của tam giác)
Suy ra:
(gt)
(theo cách vẽ)
nên D là trung điểm của AE.
Trong có:
+)
+) là trung điểm của
là đường trung bình của
là trung điểm của
Nên
Bài 35 Trang 84 SBT Toán Tập 1 Hình thang có đáy Gọi theo thứ tự là trung điểm của Chứng minh rằng ba điểm thẳng hàng.
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Sử dụng tiên đề Ơ-clit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải:
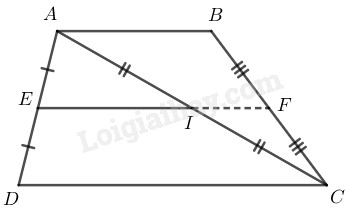
Hình thang có
là trung điểm của
là trung điểm của
Nên là đường trung bình của hình thang
(tính chất đường trung bình hình thang)
Trong có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của
(tính chất đường trung bình tam giác)
Từ và theo tiên đề Ơclít ta có đường thẳng và trùng nhau
Vậy thẳng hàng.
Bài 36 Tranh 84 SBT Toán 8 Tập 1 Cho tứ giác Gọi theo thứ tự là trung điểm của Chứng minh rằng:
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Sử dụng bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Lời giải:
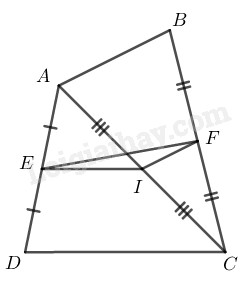
Trong tam giác ta có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của
(tính chất đường trung bình của tam giác) và
Trong tam giác ta có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của
(tính chất đường trung bình của tam giác) và
Trong ta có: (dấu xảy ra khi thẳng hàng)
Mà (chứng minh trên)
Vậy (dấu bằng xảy ra khi )
Bài 37 Trang 84 sBT Toán 8 Tập 1 Cho hình thang là trung điểm của là trung điểm của Gọi theo thứ tự là giao điểm của với Cho biết Tính các độ dài
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
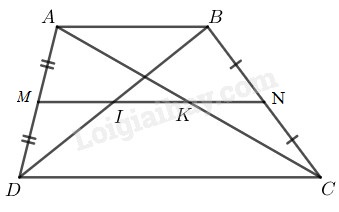
Hình thang có
là trung điểm của
là trung điểm của
Nên là đường trung bình của hình thang
và
Trong tam giác ta có:
là trung điểm của
(đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba)
Suy ra là đường trung bình của
Vậy:
Trong ta có:
là trung điểm của
Nên (đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba)
là đường trung bình của
Bài 38 Trang 84 SBT Toán 8 Tập 1 Cho tam giác các đường trung tuyến và cắt nhau ở Gọi theo thứ tự là trung điểm của Chứng minh rằng
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
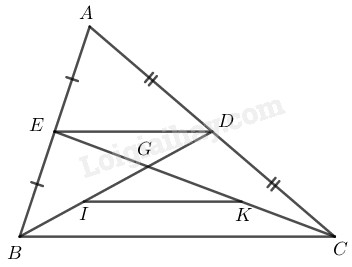
Trong tam giác ta có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của tam giác
và (tính chất đường trung bình của tam giác)
Trong tam giác ta có:
là trung điểm của
là trung điểm của
Nên là đường trung bình của
và (tính chất đường trung bình của tam giác)
Từ và suy ra: và
Bài 39 TRang 84 SBT Toán 8 Tập 1 Cho tam giác đường trung tuyến Gọi là trung điểm của là giao điểm của và Chứng minh rằng .
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
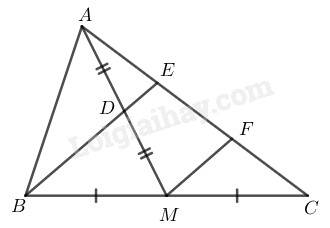
Gọi là trung điểm của
Trong ta có:
là trung điểm của cạnh
là trung điểm của cạnh
Nên là đường trung bình của
(tính chất đường trung bình của tam giác) hay
Trong tam giác ta có:
là trung điểm của
Suy ra: (tính chất đường trung bình của tam giác)
Mà nên .
Bài 40 Trang 84 SBT Toán 8 Tập 1 Cho tam giác các đường trung tuyến Gọi theo thứ tự là trung điểm của Gọi theo thứ tự là giao điểm của với Chứng minh rằng
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
Trong tam giác ta có:
là trung điểm của cạnh
là trung điểm của cạnh
Nên là đường trung bình của
và (tính chất đường trung bình của tam giác)
Vì nên tứ giác là hình thang.
Trong hình thang ta có:
là trung điểm cạnh bên
là trung điểm cạnh bên
Nên là đường trung bình hình thang
(tính chất đường trung bình hình thang)
Trong tam giác ta có:
là trung điểm của
Suy ra: là đường trung bình của
(tính chất đường trung bình tam giác)
Trong tam giác ta có:
là trung điểm của
Suy ra: là đường trung bình của
(tính chất đường trung bình tam giác)
Bài 41 Trang 84 SBT Toán 8 Tập 1 Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.
Phương pháp giải:
+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
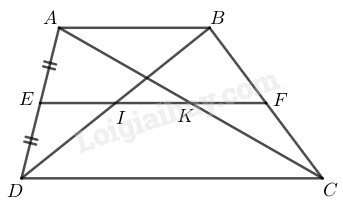
Xét hình thang có:
là trung điểm của đường thẳng đi qua song song với cắt tại tại tại
Vì là trung điểm của
Suy ra: (tính chất đường trung bình hình thang)
+) Ta có và nên
Trong tam giác ta có:
là trung điểm của
Suy ra: (tính chất đường trung bình tam giác)
Trong tam giác ta có:
là trung điểm cạnh
Suy ra: (tính chất đường trung bình của tam giác)
Vậy đường thẳng đi qua trung điểm của cạnh bên của hình thang thì đi qua trung điểm cạnh bên và trung điểm hai đường chéo
Bài 42 Trang 84 SBT Toán 8 Tập 1 Chứng minh rằng trong hình thang mà hai đáy không bằng nhau, đoạn thẳng nối trung điểm của hai đường chéo bằng nửa hiệu hai đáy.
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Sử dụng tiên đề Ơ-clit: Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải:
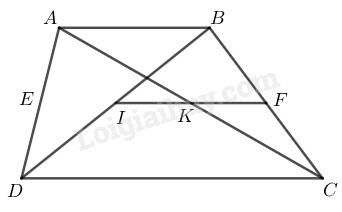
Giả sử hình thang có
lần lượt là trung điểm hai đường chéo
Gọi là trung điểm của
Trong tam giác ta có:
là trung điểm của cạnh
là trung điểm của cạnh
Nên là đường trung bình của
và (tính chất đường trung bình của tam giác)
Trong tam giác ta có:
là trung điểm của cạnh
là trung điểm của cạnh
Nên là đường trung bình của
và (tính chất đường trung bình của tam giác)
mà nên
(chứng minh trên)
Suy ra hai đường thẳng và trùng nhau.
thẳng hàng
Lại có nên nằm giữa và
Bài 43 Trang 84 SBT Toán 8 Tập 1 Hình thang có Các đường phân giác của các góc ngoài đỉnh và cắt nhau tại các đường phân giác của các góc ngoài đỉnh và cắt nhau tại
Chứng ninh rằng
Tính độ dài MN theo ( có cùng đơn vị đo)
Phương pháp giải:
+) Trong tam giác cân, đường phân giác ứng với cạnh đáy cũng là đường trung tuyến.
+) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
Lời giải:
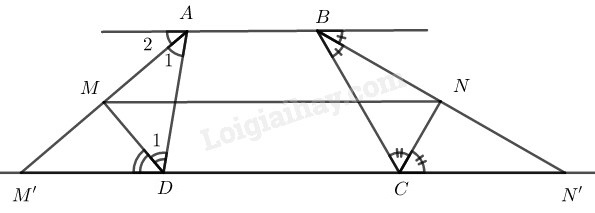
Gọi và là giao điểm của tia và với
Vì ABCD là hình thang nên hay
Suy ra cũng là hình thang.
Ta có:
Vì nên (hai góc so le trong)
(do AM' là phân giác góc ngoài tại đỉnh A)
Suy ra:
Nên cân tại
Có là phân giác của
Suy ra: là đường trung tuyến (tính chất tam giác cân)
(1)
Vì nên (hai góc so le trong)
(do BN' là phân giác góc ngoài tại đỉnh B)
Suy ra:
Nên cân tại
Có là phân giác của
Suy ra: là đường trung tuyến (tính chất tam giác cân)
(2)
Từ (1) và (2) suy ra: là đường trung bình của hình thang
(tính chất đường trung bình hình thang)
Hay
(tính chất đường trung bình của hình thang)
Mà (vì cân tại ) và (vì cân tại )
Thay vào ta được:
Bài 44 Trang 85 SBT Toán 8 Tập 1 Cho tam giác đường trung tuyến Gọi là trung điểm của Qua kẻ đường thẳng cắt các cạnh và Gọi là các đường vuông góc kẻ từ đến đường thẳng Chứng minh rằng:
Phương pháp giải:
+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
Lời giải:
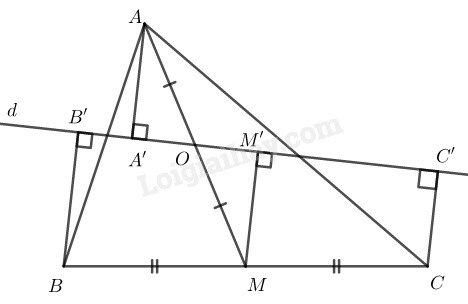
Ta có:
Suy ra:
Tứ giác là hình thang
Kẻ
Ta lại có: là trung điểm của (do AM là đường trung tuyến của tam giác ABC)
Nên là đường trung bình của hình thang
Xét tam giác vuông và tam giác vuông
(đối đỉnh)
Do đó: (cạnh huyền, góc nhọn)
Từ và suy ra: .
Bài 4.1 Trang 85 SBT Toán 8 Tập 1 Trên hình ta có và Biết Các độ dài và bằng:
và và
và và
Phương pháp giải:
+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
Lời giải:
Ta có nên tứ giác là hình thang.
là trung điểm của
là trung điểm của
là đường trung bình của hình thang
Ta có nên tứ giác là hình thang.
là trung điểm của
là trung điểm của
là đường trung bình của hình thang
Chọn và
Bài 4.2 Trang 85 SBT Toán 8 Tập 1 Cho đường thẳng và hai điểm có khoảng cách đến đường thẳng theo thứ tự là và Gọi là trung điểm của Tính khoảng cách từ đến đường thẳng
Phương pháp giải:
* Chú ý: Chia hai trường hợp: cùng phía với và khác phía với
Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang:
+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
Trường hợp và nằm trên một nửa mặt phẳng bờ chứa đường thẳng
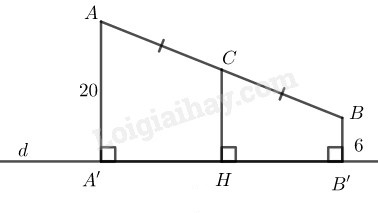
Gọi là chân đường vuông góc kẻ từ và đến
Tứ giác là hình thang. Kẻ
mà là trung điểm của nên là đường trung bình của hình thang
Trường hợp và nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng
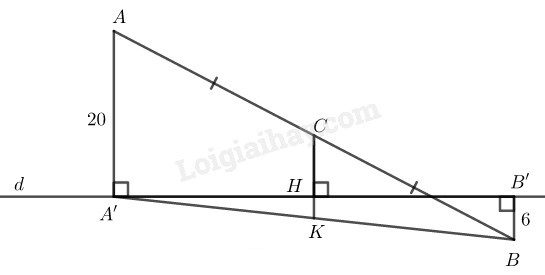
Kẻ cắt tại
Trong ta có:
Mà nên và là đường trung bình của tam giác
(tính chất đường trung bình của tam giác)
Trong có và
Nên là đường trung bình của
(tính chất đường trung bình của tam giác)
Bài 4.3 Trang 85 SBT Toán 8 Tập 1 Cho tam giác Gọi là trung điểm của Trên tia đối của tia lấy điểm sao cho Gọi là giao điểm của và Chứng minh rằng
Phương pháp giải:
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
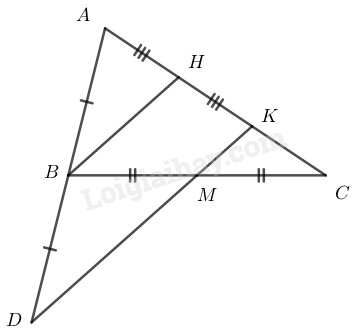
Gọi là trung điểm của
Trong ta có:
là trung điểm của
là trung điểm của ( )
là đường trung bình của
(tính chất đường trung bình của tam giác)
Hay
Trong ta có là trung điểm của
Suy ra: (vì
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.