Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 5: Dựng hình bằng thước và compa. Dựng hình thang chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 5: Dựng hình bằng thước và compa. Dựng hình thang

Bài 45 Trang 85 SBT Toán 8 Tập 1 Dựng tam giác $ABC$ vuông tại $A,$ biết cạnh huyền $BC=5cm$ và $\hat{B}={35}^0$.

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

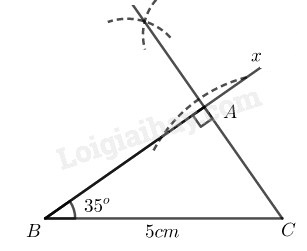
Cách dựng:

-  Dựng đoạn $BC=5cm$

-  Dựng $\widehat{CBx}={35}^0$

-  Dựng $CA\perp Bx$ tại $A,$ ta có $∆ABC$ dựng được.

Chứng minh:

$∆ABC$ có $\hat{A}={90}^0,\hat{B}={35}^0,$ $BC=5cm.$ Thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.

Bài 46 Trang 85 SBT Toán 8 Tập 1 Dựng tam giác $ABC$ vuông tại $A,$ biết cạnh huyền $BC=4,5cm$ và cạnh góc vuông $AC=2cm.$

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

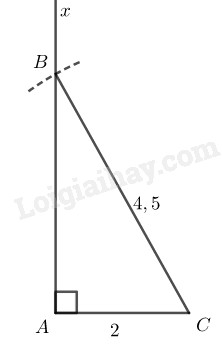
Cách dựng:

-   Dựng đoạn $AC=2cm$

-   Dựng $\widehat{CAx}={90}^0$

-   Dựng cung tròn tâm $C$ bán kính $4,5cm$ cắt $Ax$ tại $B.$ Nối $CB$ ta có $∆ABC$ cần dựng

Chứng minh:

$∆ABC$ có $\hat{A}={90}^0,$ $AC=2cm,$ $BC=4,5cm.$ Thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.

Bài 47 Trang 85 SBT Toán 8 Tập 1 Dựng góc ${30}^0$ bằng thước và compa.

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

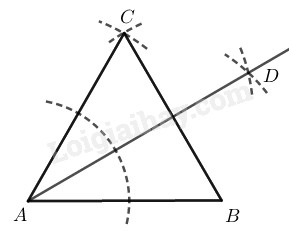
Cách dựng:

-  Dựng tam giác đều $ABC$

-  Dựng tia phân giác $AD$ của $\widehat{BAC}$ 

Ta có $\widehat{BAD}={30}^0$

Chứng minh: $∆ABC$ đều

$\Rightarrow \widehat{BAC}={60}^0$

$\widehat{BAD}={\displaystyle \frac{\widehat{BAC}}{2}}$ (tính chất tia phân giác)

$\Rightarrow \widehat{BAD}={30}^0$

Biện luận: Ta luôn dựng được một góc thỏa mãn điều kiện của đề bài.

Bài 48 Trang 85 SBT Toán 8 Tập 1 Dựng hình thang cân $ABCD$ $(AB//CD),$ biết $CD=3cm,$ $AC=4cm,$ $\hat{D}={70}^0$.

Phương pháp giải:

* Phân tích: 

     +) Giả sử đã có một hình thỏa mãn điều kiện bài toán

     +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

     +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

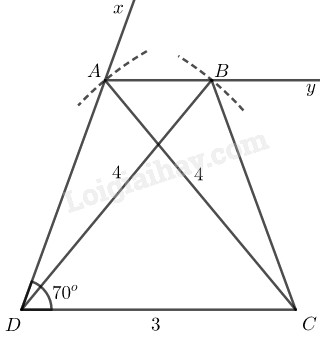
Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiên bài toán, ta thấy $∆ACD$ xác định được vì biết $CD=3cm,$ $\hat{D}={70}^0,$ $AC=4cm.$

Ta cần xác định đỉnh $B.$ Đỉnh $B$ thỏa mãn hai điều kiện:

- Nằm trên tia $Ay//CD$

- $B$ cách $D$ một khoảng bằng $4cm$

Cách dựng:

- Dựng đoạn $CD=3cm$

- Dựng $\widehat{CDx}={70}^0$

- Trên nửa mặt phẳng bờ $CD$ chứa tia $Dx$ dựng cung tròn tâm $C$ bán kính $4cm$ cắt $Dx$ tại $A.$

- Dựng tia $Ay//CD$

- Trên nửa mặt phẳng bờ $CD$ chứa điểm $A,$ dựng cung tròn tâm $D$ bán kính $4cm$ cắt $Ay$ tại $B$

- Nối $BC$ ta có hình thang $ABCD$ cần dựng.

Chứng minh: Thật vậy theo cách dựng ta có $AB//CD$ nên tứ giác $ABCD$ là hình thang có $CD=3cm,$ $\widehat{ADC}={70}^0,$ $AC=BD=4cm.$

Vậy $ABCD$ là hình thang cân.

Biện luận:

$∆ACD$ luôn dựng được nên hình thang $ABCD$ luôn dựng được.

Bài toán có một nghiệm hình.

Bài 49 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang $ABCD$ $(AB//CD),$ biết $\hat{D}={90}^0,$ $AD=2cm,$ $CD=4cm,$ $BC=3cm.$

Phương pháp giải:

* Phân tích: 

+) Giả sử đã có một hình thỏa mãn điều kiện bài toán

+) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

+) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải: 

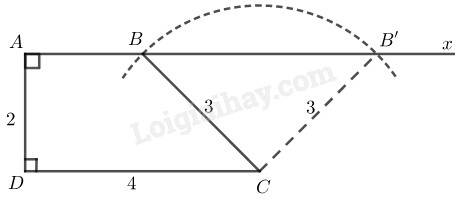
Phân tích:

Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán.

Ta thấy $∆ADC$ xác định được vì biết $AD=2cm,$ $\hat{D}={90}^0,$ $DC=4cm.$ Ta cần xác định đỉnh $B.$ Đỉnh $B$ thỏa mãn hai điều kiện:

- $B$ nằm trên tia $Ax//CD.$

- $B$ cách $C$ một khoảng bằng $3cm.$

Cách dựng:

- Dựng $∆ADC$ biết $AD=2cm,$ $\hat{D}={90}^0,$ $DC=4cm.$

- Dựng $Ax\perp AD$

- Dựng cung tròn tâm $C$ bán kính bằng $3cm,$ cắt $Ax$ tại $B.$

Nối $BC$ ta có hình thang $ABCD$ dựng được.

Chứng minh: Thật vậy theo cách dựng, ta có: $AB//CD,$ $\hat{D}={90}^0$

Tứ giác $ABCD$ là hình thang vuông.

Lại có $AD=2cm,$ $CD=4cm,$ $BC=3cm.$

Hình thang dựng được thỏa mãn điều kiện bài toán.

Biện luận: $∆ADC$ dựng được, hình thang $ABCD$ luôn dựng được.

Bài toán có hai nghiệm hình.

Bài 50 Trang 86 SBT Toán 8 Tập 1 Dựng tam giác $ABC$ cân tại $A,$ biết $BC=3cm,$ đường cao $BH=2,5cm.$

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài.

Lời giải: 

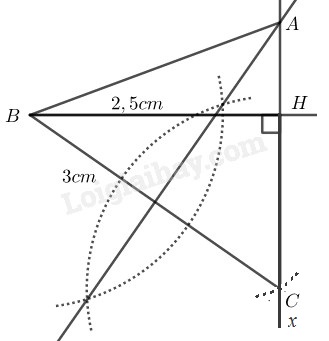
Cách dựng:

- Dựng $BH=2,5cm$

- Dựng $\widehat{xHB}={90}^0$

- Dựng cung tròn tâm $B$ bán kính $3cm$ cắt $Hx$ tại $C$

- Dựng $BC$

- Dựng đường trung trực $BC$ cắt $CH$ tại $A$

- Dựng $AB,$ ta có $∆ABC$ cần dựng.

Chứng minh: Ta có $AC=AB$ ( tính chất đường trung trực)

Nên $∆ABC$ cân tại $A,$ $BH\perp AC$

Ta lại có $BC=3cm,$ $BH=2,5cm.$

Vậy $∆ABC$ dựng được thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.

Bài 51 Trang 86 SBT Toán 8 Tập 1 Dựng tam giác $ABC,$ biết $\hat{B}={40}^0,$ $BC=4cm,$ $AC=3cm.$

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

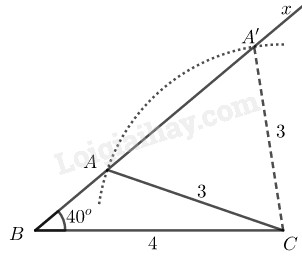
Cách dựng:

- Dựng đoạn thẳng $BC=4cm$

- Dựng $\widehat{CBx}={40}^0$

- Dựng trên nửa mặt phẳng bờ $BC$ chứa tia $Bx$ cung tròn tâm $C$ bán kính $3cm$ cắt $Bx$ tại $A$

- Kẻ $AC,$ ta có tam giác $ABC$ cần dựng.

Chứng minh: Thật vậy theo cách dựng $∆ABC$ có $BC=4cm,$ $\hat{B}={40}^0,$ $AC=3cm.$

Thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được hai tam giác thỏa mãn điều kiện của đề bài.

Bài 52 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang $ABCD$ $(AB//CD),$ biết $AD=2cm,$ $CD=4cm,$ $BC=2,5cm,$ $AC=3,5cm.$

Phương pháp giải:

* Phân tích: 

+) Giả sử đã có một hình thỏa mãn điều kiện bài toán

+) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

+) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải: 

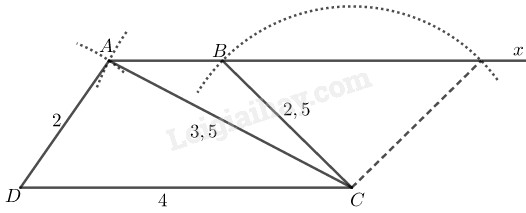
Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán. Tam giác $ADC$ dựng được vì biết ba cạnh $AD=2cm,$ $DC=4cm,$ $AC=3,5cm.$

Điểm $B$ thỏa mãn hai điều kiện:

- $B$ nằm trên đường thẳng đi qua $A$ và song song với $CD.$

- $B$ cách $C$ một khoảng bằng $2,5cm$

Cách dựng:

- Dựng $∆ADC$ biết $AD=2cm,$ $DC=4cm,$ $AC=3,5cm$

- Dựng tia $Ax//CD.$ $Ax$ nằm trong nửa mặt phẳng bờ $AD$ chứa điểm $C.$

- Dựng cung tròn tâm $C$ bán kính $2,5cm.$ Cung này cắt $Ax$ tại $B,$ nối $CB$ ta có hình thang $ABCD$ cần dựng.

Chứng minh:

Tứ giác $ABCD$ là hình thang vì $AB//CD$

Hình thang $ABCD$ có: $AD=2cm,$ $CD=4cm,$ $AC=3,5cm,$ $BC=2,5cm$ thỏa mãn yêu cầu bài toán.

Biện luận: $∆ADC$ luôn dựng được nên hình thang $ABCD$ dựng được.

Vì cung tròn tâm $C$ bán kính $3cm$ cắt $Ax$ tại hai điểm nên ta dựng được hai hình thang thỏa mãn bài toán.

Bài 53 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang cân $ABCD$ $(AB//CD),$ biết $AD=2cm,$ $CD=4cm,$ $AC=3,5cm.$

Phương pháp giải:

* Phân tích: 

     +) Giả sử đã có một hình thỏa mãn điều kiện bài toán

     +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

     +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

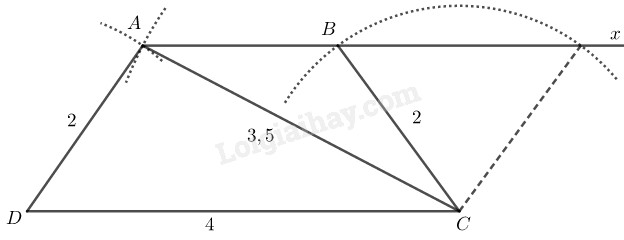
Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán. Tam giác $ADC$ dựng được vì biết ba cạnh $AD=2cm,$ $CD=4cm,$ $AC=3,5cm.$ Điểm $B$ thỏa mãn $2$ điều kiện:

- $B$ nằm trên đường thẳng đi qua $A$ và song song với $CD$

- $B$ cách $D$ một khoảng bằng $3,5cm$

Cách dựng:

- Dựng tam giác $ADC$ biết $AD=2cm,$ $AC=3,5cm,$ $CD=4cm$

- Dựng tia $Ax//CD,$ $Ax$ nằm trong nửa mặt phẳng bờ $AD$ chứa điểm $C$

- Dựng cung tròn tâm $D$ bán kính $3,5cm.$ Cung này cắt $Ax$ tại $B.$ Nối $CB$ ta có hình thang $ABCD$ cần dựng.

Chứng minh:

Tứ giác $ABCD$ là hình thang vì $AB//CD.$

$AC=BD=3,5cm$

Vậy hình thang $ABCD$ là hình thang cân.

Hình thang cân $ABCD$ có: $AD=2cm,$ $CD=4cm,$ $AC=3,5cm$ thỏa mãn yêu cầu bài toán.

Biện luận: Tam giác $ADC$ luôn dựng được nên hình thang $ABCD$ luôn dựng được. Cung tròn tâm $D$ bán kính $3,5cm$ cắt $Ax$ tại $1$ điểm nên ta dựng được một hình thang thỏa mãn yêu cầu bài toán.

Bài 54 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang cân $ABCD$ $(AB//CD),$ biết hai đáy $AB=2cm,$ $CD=4cm,$ đường cao $AH=2cm.$

Phương pháp giải:

* Phân tích: 

     +) Giả sử đã có một hình thỏa mãn điều kiện bài toán

     +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

     +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán. Tam giác $ADH$ dựng được vì biết hai cạnh góc vuông $AH=2cm$ và $HD=1cm,$ $\hat{H}={90}^0$. Vì đáy $AB<CD$ nên $\hat{D}<{90}^0$. Điểm $H$ nằm giữa $D$ và $C$.

Điểm $C$ nằm trên tia đối tia $HD$ và cách $H$ một khoảng bằng $3cm$

Điểm $B$ thỏa mãn hai điều kiện:

- $B$ nằm trên đường thẳng đi qua $A$ và song song với $DH.$

- $B$ cách $A$ một khoảng bằng $2cm$

Cách dựng:

- Dựng $∆AHD$ biết $\hat{H}={90}^0,$ $AH=2cm,$ $HD=1cm$

- Dựng tia đối của tia $HD$

- Trên tia đối của tia $HD,$ dựng điểm $C$ sao cho $HC=3cm$

- Dựng tia $Ax//DH,$ $Ax$ nằm trên nửa mặt phẳng bờ $AD$ chứa điểm $H$

- Dựng điểm $B$ trên tia $Ax$ sao cho $AB=2cm.$ Nối $CB$ ta có hình thang $ABCD$ cần dựng.

Chứng minh:

Tứ giác $ABCD$ là hình thang vì $AB//CD$

Kẻ $BK\perp CD.$ Tứ giác $ABKH$ là hình thang có hai cạnh bên song song

Nên :   $BK=AH$ và $KH=AB$

Suy ra: $KC=HC–KH=HC–AB$$=3-2=1(cm)$

Vì $AH=BK$ và $KC=DH(=1cm)$

Suy ra hai tam giác vuông: $∆AHD=∆BKC(c.g.c)$ $\Rightarrow \hat{D}=\hat{C}$

Vậy hình thang $ABCD$ là hình thang cân.

Hình thang cân $ABCD$ có: $AH=2cm,$ đáy $AB=2cm,$ đáy $CD=4cm$

Thỏa mãn điều kiện bài toán.

Biện luận: Tam giác $AHD$ luôn dựng được nên hình thang $ABCD$ luôn dựng được. Ta luôn dựng được một hình thang thỏa mãn điều kiện bài toán.

Bài 55 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang $ABCD,$ biết hai đáy $AB=2cm,$ $CD=4cm,$ $\hat{C}={50}^0,\hat{D}={70}^0$.

Phương pháp giải:

* Phân tích: 

     +) Giả sử đã có một hình thỏa mãn điều kiện bài toán

     +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

     +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

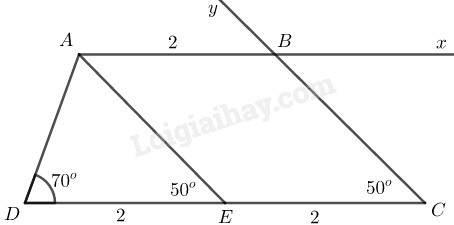
Phân tích: Giả sử hình thang $ABCD$ thỏa mãn yêu cầu bài toán. Qua $A$ kẻ đường thẳng song song với $BC$ cắt $CD$ tại $E.$ Hình thang $ABCE$ có hai cạnh bên song song nên $AB=EC=2cm$ do đó $DE=2cm$

Tam giác $ADE$ dựng được vì biết $2$ góc kề với một cạnh.

Điểm $C$ nằm trên tia $DE$ cách $D$ một khoảng bằng $4cm$

Điểm $B$ thỏa mãn hai điều kiện:

- $B$ nằm trên đường thẳng đi qua $A$ và song song với $CD.$

- $B$ nằm trên đường thẳng đi qua $C$ và song song với $AE.$

Cách dựng:

- Dựng tam giác $ADE$ biết $DE=2cm,$ $\hat{D}={70}^0,$$\hat{E}={50}^0$ 

- Trên tia $DE$ lấy điểm $C$ sao cho $DC=4cm$

- Dựng tia $Ax//CD,$ $Ax$ nằm trên nửa mặt phẳng bờ $AD$ chứa điểm $C$

- Dựng tia $Cy//AE,$ $Cy$ nằm trên nửa mặt phẳng bờ $CD$ chứa điểm $A.$ $Cy$ cắt $Ax$ tại $B.$ Hình thang $ABCD$ cần dựng.

Chứng minh:

Tứ giác $ABCD$ là hình thang vì $AB//CD$

$CD=CE+ED$$\Rightarrow CE=CD–ED$$=4–2=2(cm)$

Hình thang $ABCE$ có hai cạnh bên $AE//CB$

$\Rightarrow AB=CE=2(cm)$

$\hat{C}=\hat{E}={50}^0$ (hai góc đồng vị)

$\hat{D}={70}^0$

Hình thang $ABCD$ thỏa mãn điều kiện bài toán.

Biện luận: Tam giác $ADE$ luôn dựng được, hình thang $ABCD$ luôn dựng được. Ta dựng được một hình thang thỏa mãn điều kiện bài toán.

Bài 56 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang $ABCD,$ biết hai đáy $AB=1cm,$ $CD=4cm,$ hai cạnh bên $AD=2cm,$ $BC=3cm.$

Phương pháp giải:

* Phân tích: 

     +) Giả sử đã có một hình thỏa mãn điều kiện bài toán

     +) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

     +) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

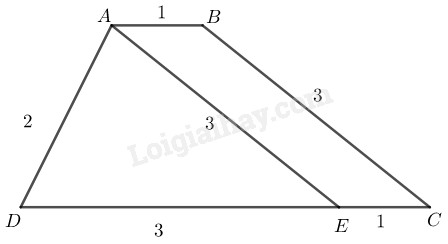
Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán.

Qua $A$ kẻ đường thẳng song song với $BC$ cắt $CD$ tại $E$ ta thấy tam giác $AED$ xác định vì biết ba cạnh, ta cần xác định đỉnh $B$ và $C$

- Đỉnh $C$ nằm trên tia $DE,$ cách $D$ một khoảng bẳng $4cm$

- Đỉnh $B$ nằm trên đường thẳng đi qua $A$ song song với đường thẳng $DE$ và cách $A$ một khoảng bằng $1cm.$

Cách dựng:

- Dựng $∆ADE$ biết $AD=2cm,$ $DE=3cm,$ $AE=3cm$

- Trên tia $DE$ dựng điểm $C$ sao cho $DC=4cm$

- Dựng đường thẳng đi qua $A$ và song song với $DC,$ lấy điểm $B$ sao cho $AB=1cm.$ Nối $BC$ ta có hình thang $ABCD$ cần dựng

Chứng minh: Thật vậy theo cách dựng ta có $AB//CD$ nên tứ giác $ABCD$ là hình thang.

Ta có: $AD=2cm,$ $DC=4cm,$ $AB=1cm,$ hình thang $ABCE$ có hai cạnh đáy $AB=EC=1cm$ nên $BC=AE=3cm.$

Hình thang $ABCD$ thỏa mãn điều kiện bài toán.

Biện luận: Tam giác $ADE$ luôn dựng được nên hình thang $ABCD$ dựng được, bài toán có một nghiệm hình.

Bài 57 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang cân $ABCD,$ biết hai đáy $AB=1cm,$ $CD=3cm,$ đường chéo $BD=3cm.$

Phương pháp giải:

* Phân tích: 

+) Giả sử đã có một hình thỏa mãn điều kiện bài toán

+) Chọn ra các yếu tố dựng được ngay (đoạn thẳng, tam giác,...)

+) Đưa việc dựng các điểm còn lại về các phép dựng hình cơ bản và các bài toán dựng hình cơ bản (Mỗi điểm thường được xác định là giao của hai đường.)

* Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

* Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

* Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

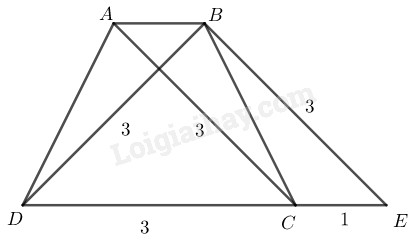
Phân tích: Giả sử hình thang $ABCD$ dựng được thỏa mãn điều kiện bài toán.

Từ $B$ kẻ đường thẳng song song với $AC$ cắt $CD$ tại $E.$ Tứ giác $ABEC$ là hình thang có hai cạnh bên song song nên $CE=AB=1cm,$ $BE=AC=3cm$

Tam giác $BDE$ xác định được, ta cần xác định đỉnh $C$ và $A$

- Đỉnh $C$ nằm trên tia $DE$ cách $D$ một khoảng bẳng $3cm$

- Đỉnh $A$ nằm trên đường thẳng đi qua $B$ và song song với $CD,$ $A$ cách $C$ một khoảng bằng $3cm$

Cách dựng:

- Dựng $∆BDE$ biết $BD=3cm,$ $BE=3cm,$ $DE=4cm.$

- Dựng điểm $C$ trên tia $DE$ sao cho $DC=3cm$

- Dựng đường thẳng $d$ đi qua $B$ song song với $CD$

- Dựng cung tròn tâm $C$ bán kính $3cm$ cắt đường thẳng $d$ tại $A.$

Nối $AD$ ta có hình thang $ABCD$ dựng được.

Chứng minh: Thật vậy theo cách dựng ta có $AB//CD.$

Tứ giác $ABCD$ là hình thang

$CD=3cm,$ $AC=BD=3cm.$ Vậy $ABCD$ là hình thang cân

Thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

Bài 58 Trang 86 SBT Toán 8 Tập 1 Dựng tứ giác $ABCD,$ biết $AB=2cm,$ $AD=3cm,$ $\hat{A}={80}^0,$$\hat{B}={120}^0,$$\hat{C}={100}^0$.

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

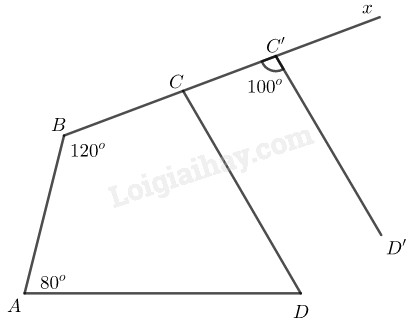
Cách dựng:

- Dựng $∆ABD$ biết $AB=2cm,$ $\hat{A}={80}^0,$ $AD=3cm.$

- Dựng $\widehat{ABx}={120}^0$ ($Bx$ và $D$ thuộc cùng một nửa mặt phẳng bờ $AB$)

- Lấy điểm $C^{\prime }$ bất kì trên tia $Bx$

- Dựng $\widehat{B{C}^{\prime }{D}^{\prime }}={100}^0$ ($C^{\prime }{D}^{\prime }$ và $D$ thuộc cùng một nửa mặt phẳng bờ $BC$)

- Qua $D$ dựng đường thẳng song song với $C^{\prime }{D}^{\prime }$, cắt $Bx$ ở $C.$ Ta được tứ giác $ABCD$ cần dựng.

Chứng minh: Thật vậy theo cách dựng $AB=2cm,$ $\hat{A}={80}^0,$ $AD=3cm,$ $\hat{B}={120}^0,$  $\hat{C}=\widehat{C^{\prime }}={100}^0$ (hai góc đồng vị)

Tứ giác $ABCD$ dựng được thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

Bài 59 Trang 86 SBT Toán 8 Tập 1 Dựng góc ${75}^0$ bằng thước và compa.

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

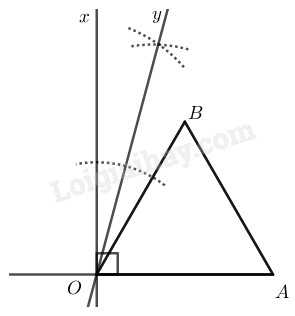
Cách dựng:

- Dựng tam giác $ABC$ đều

- Trên nửa mặt phẳng bờ $AC$ chứa điểm $B$ dựng tia $Ax\perp AC$

- Dựng tia phân giác $Ay$ của $\widehat{xAB}$ ta có $\widehat{CAy}={75}^0$

Chứng minh:

Thật vậy $∆ABC$ đều nên $\widehat{BAC}={60}^0,\widehat{xAC}={90}^0$ 

$\Rightarrow \widehat{BAx}=\widehat{xAC}-\widehat{BAC}$$={90}^0-{60}^0={30}^0$
$\widehat{BAy}={\displaystyle \frac{1}{2}\widehat{BAx}={15}^0}$ (do  $Ay$ là tia phân giác của $\widehat{xAB})$ 

$\Rightarrow \widehat{CAy}=\widehat{BAC}+\widehat{BAy}$$={60}^0+{15}^0={75}^0$

Biện luận: Ta luôn dựng được một góc thỏa mãn điều kiện của đề bài.

Bài 5.1 Trang 86 SBT Toán 8 Tập 1 Dựng hình thang cân $ABCD$ $(AB//CD)$ biết $BC=3cm,$ $AC=2cm,$ đường cao bằng $2,5cm.$

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

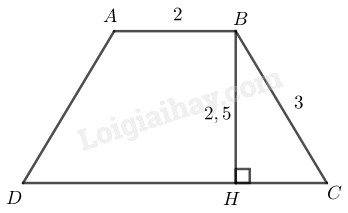
Cách dựng:

-  Dựng $∆BHC$ có $BH=2,5cm$, $\widehat{BHC}={90}^0$ và $BC=3cm$

-  Dựng tia đi qua $B$ và song song $CH$ nằm trên nửa mặt phẳng bờ $BC$ chứa điểm $H.$ Trên tia này, lấy điểm $A$ sao cho $BA=2cm$

-  Dựng cung tròn tâm $B$ bán kính bằng $AC$ cắt đường thẳng $CH$ tại $D.$

Nối $AD$ ta có hình thang $ABCD$ cần dựng.

Chứng minh:

Thật vậy theo cách dựng $AB//CD$ nên tứ giác $ABCD$ là hình thang có $AB=2cm,$ $BC=3cm,$ $BH=2,5cm,$$AC=BD$

Vậy $ABCD$ là hình thang cân thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

Bài 5.2 Trang 86 SBT Toán 8 Tập 1 Dựng tam giác $ABC$ biết $\hat{B}={80}^0,$ $BC=3cm,$ $AB+AC=5cm.$

Phương pháp giải:

+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.

+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.

+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài

Lời giải:

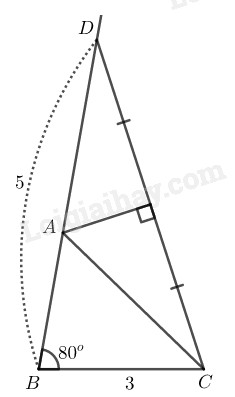
Cách dựng:

- Dựng tam giác $DBC$ có $\hat{B}={80}^0,$ $BC=3cm,$ $BD=5cm.$

- Dựng đường trung trực của $CD$ cắt $BD$ tại $A$

Nối $A$ với $C$ ta có $∆ABC$ cần dựng

Chứng minh: Thật vậy theo cách dựng thì $∆ABC$ có:

$\hat{B}={80}^0,$ $BC=3cm,$ $AB+AC=AB+AD=CD=5cm$ (vì $AC=AD$ tính chất đường trung trực nên $AB+AC=5cm$)

$∆ABC$ thỏa mãn điều kiện bài toán.

Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.