Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 7: Hình bình hànhi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 7: Hình bình hành
Bài 73 Trang 89 SBT Toán 8 Tập 1 Các tứ giác vẽ trên giấy kẻ ô vuông ở hình có là hình bình hành không
Phương pháp giải:
Dấu hiệu nhận biết:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Lời giải:
Tứ giác là hình bình hành vì có cạnh đối và bằng cạnh ô vuông.
Tứ giác là hình bình hành vì có các cạnh đối bằng nhau.
là đường chéo hình chữ nhật có cạnh ô vuông và cạnh ô vuông
là đường chéo hình chữ nhật có cạnh ô vuông và cạnh ô vuông.
Bài 74 Trang 89 SBT Toán 8 Tập 1 Cho hình bình hành Gọi là trung điểm của là trung điểm của Chứng minh rằng
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
Dấu hiệu nhận biết:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải:
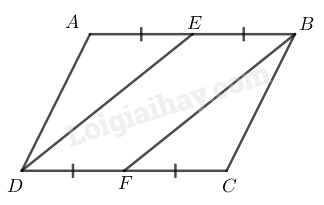
Vì ABCD là hình bình hành nên ( tính chất hình bình hành)
Lại có E là trung điểm cạnh AB và F là trung điểm cạnh CD nên:
Suy ra: (vì
Mà
Từ và suy ra tứ giác là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
(tính chất hình bình hành)
Bài 75 Trang 89 SBT Toán 8 Tập 1 Cho hình bình hành Tia phân giác của góc cắt ở Tia phân giác của góc cắt ở Chứng minh rằng là hình bình hành.
Phương pháp giải:
Sử dụng kiến thức: Trong hình bình hành, hai góc đối bằng nhau.
Dấu hiệu nhận biết: Tứ giác có các cạnh đối song song là hình bình hành.
Lời giải:
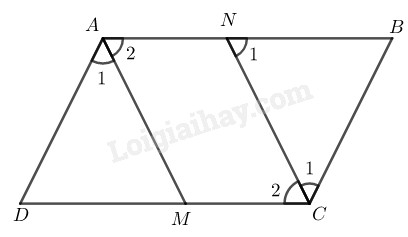
Vì ABCD là hình bình hành nên (tính chất hình bình hành)
(do AM là tia phân giác của góc BAD)
(do CN là tia phân giác của góc BCD)
Suy ra: (vì
Lại có (do ABCD là hình bình hành)
Nên
Mà (so le trong)
Suy ra:
( vì có các cặp góc ở vị trí đồng vị bằng nhau)
Từ và suy ra: Tứ giác là hình bình hành ( theo định nghĩa)
Bài 76 Trang 89 SBT Toán 8 Tập 1 Trên hình cho là hình bình hành. Chứng minh rằng là hình bình hành.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải:
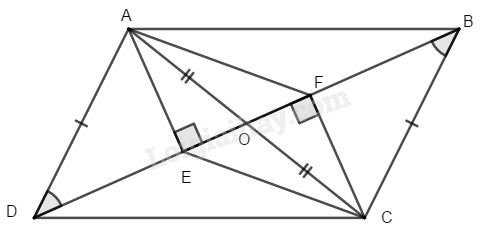
Gọi là giao điểm của và
Vì ABCD là hình bình hành nên ( tính chất hình bình hành)
Xét hai tam giác vuông và ta có:
( chứng minh trên)
(đối đỉnh)
Do đó ( cạnh huyền, góc nhọn)
Từ và suy ra tứ giác là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Bài 77 Trang 89 SBT Toán 8 Tập 1 Tứ giác có theo thứ tự là trung điểm của các cạnh Tứ giác là hình gì Vì sao
Phương pháp giải:
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải:
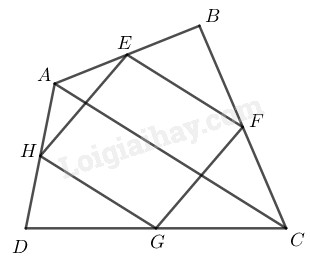
Nối đường chéo
Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình tam giác)
Trong ta có:
là trung điểm của
là trung điểm của
nên là đường trung bình của
và (tính chất đường trung bình tam giác)
Từ và suy ra: và
Vậy tứ giác là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
Bài 78 Trang 89 SBT Toán 8 Tập 1 Cho hình bình hành Gọi theo thứ tự là trung điểm của Đường chéo cắt theo thứ tự ở Chứng minh rằng:
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Lời giải:
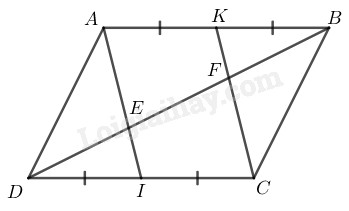
Vì ABCD là hình bình hành nên ( tính chất hình bình hành)
(do K là trung điểm của AB)
(do I là trung điểm của DC)
Suy ra: (vì
Mặt khác: (do ABCD là hình bình hành)
Từ và suy ra tứ giác là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
Trong ta có:
là trung điểm của
hay nên ( tính chất đường trung bình tam giác)
Trong ta có:
là trung điểm của
hay nên (tính chất đường trung bình tam giác)
Suy ra:
Bài 79 Trang 89 SBT Toán 8 Tập 1 Đề bài
Tính các góc của hình bình hành biết:
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai góc đối bằng nhau.
+) Trong hình bình hành, hai góc kề một cạnh bù nhau.
Lời giải:
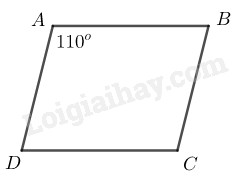
Tứ giác là hình bình hành
(tính chất hình bình hành)
Ta có: (do ABCD là hình bình hành)
Nên (hai góc trong cùng phía bù nhau)
(tính chất hình bình hành)
Tứ giác là hình bình hành nên
( góc trong cùng phía bù nhau)
Suy ra:
( tính chất hình bình hành)
(tính chất hình bình hành)
Bài 80 Trang 89 SBT Toán 8 Tập 1 Trong các tứ giác trên hình tứ giác nào là hình bình hành
Phương pháp giải:
Dấu hiệu nhận biết:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tứ giác có các góc đối bằng nhau là hình bình hành.
Lời giải:
+) Tứ giác là hình bình hành vì và
+) Xét tứ giác , theo định lý tổng 4 góc trong tứ giác ta có:
Tứ giác là hình bình hành vì có
.
+) Tứ giác không là hình bình hành vì có hai đường chéo không cắt nhau tại trung điểm mỗi đường.
Bài 81 Trang 90 SBT Toán 8 Tập 1 Chu vi hình bình hành bằng chu vi tam giác bằng Tính độ dài
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
+) Chu vi tứ giác bằng tổng 4 cạnh, chu vi tam giác bằng tổng 3 cạnh.
Lời giải:
Vì ABCD là hình bình hành nên (tính chất)
Chu vi hình bình hành là
Mà chu vi hình bình hành bằng (giả thiết)
Nên
Chu vi của bằng :
Bài 82 Trang 90 SBT Toán 8 Tập 1 Trên hình cho là hình bình hành. Chứng minh rằng
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Lời giải:
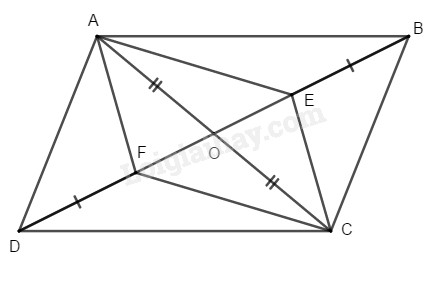
Gọi là giao điểm của và
(tính chất hình bình hành)
(tính chất hình bình hành)
Ta có:
Suy ra:
Do đó tứ giác là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Suy ra (tính chất hình bình hành).
Bài 83 Trang 90 SBT Toán 8 Tập 1 Cho hình bình hành Gọi theo thứ tự là trung điểm của Gọi là giao điểm của và là giao điểm của và Chứng minh rằng :
là hình bình hành.
Các đường thẳng đồng quy.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải:
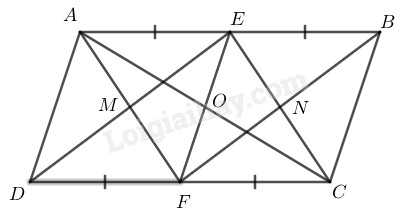
Vì ABCD là hình bình hành nên và (tính chất)
Ta có: (vì E là trung điểm của AB)
(vì F là trung điểm của CD)
Mà (cmt)
Suy ra
Xét tứ giác có:
(cmt)
(do
Suy ra tứ giác là hình bình hành ( vì có một cặp cạnh đối diện song song và bằng nhau)
hay
Xét tứ giác có:
(cmt)
(do )
Suy ra tứ giác là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
hay
Từ và suy ra tứ giác là hình bình hành (theo định nghĩa)
Gọi là giao điểm của và
Tứ giác là hình bình hành
Tứ giác là hình bình hành nên hai đường chéo cắt nhau tại trung điểm mỗi đường.
Suy ra: đi qua trung điểm của
Vậy đồng quy tại
Bài 84 Trang 90 SBT Toán 8 Tập 1 Trên hình cho là hình bình hành. Chứng minh rằng:
là hình bình hành
Các đường thẳng đồng quy.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai góc đối bằng nhau.
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải:
Vì ABCD là hình bình hành nên (tính chất)
+) Ta có: mà (gt) nên
+) Ta có: mà (gt) nên
Xét và
(gt)
(tính chất hình bình hành ABCD)
(cmt)
Do đó:
(1)
Xét và
(tính chất hình bình hành ABCD)
(cmt)
Do đó:
(2)
Từ (1) và (2) suy ra: Tứ giác là hình bình hành (vì có các cặp cạnh đối bằng nhau)
Gọi là giao điểm của và
Xét tứ giác có:
(do và
Suy ra: Tứ giác là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
là trung điểm của và
Tứ giác là hình bình hành có là trung điểm của nên cũng là trung điểm của
Tứ giác là hình bình hành có là trung điểm của nên cùng là trung điểm của
Vậy đồng quy tại
Bài 85 Trang 90 SBT Toán 8 Tập 1 Cho hình bình hành Qua kẻ đường thẳng chỉ có một điểm chung với hình bình hành. Gọi là các đường vuông góc kẻ từ đến đường thẳng Chứng minh rằng
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
Lời giải:
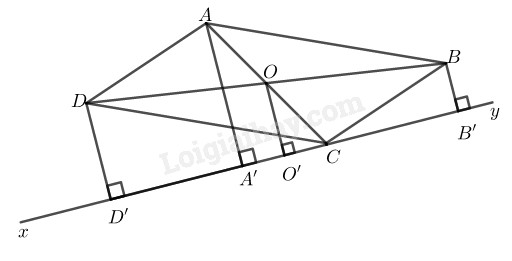
Gọi là giao điểm của hai đường chéo và
Kẻ
Ta có:
Suy ra:
Tứ giác là hình thang
(tính chất hình bình hành)
nên do đó là đường trung bình của hình thang
(tính chất đường trung bình hình thang)
Hay
(theo cách vẽ)
Suy ra:
Trong ta có: ( tính chất hình bình hành) và nên
Suy ra là đường trung bình của
(tính chất đường trung bình của tam giác)
Từ và suy ra:
Bài 86 Trang 90 SBT Toán 8 Tập 1 Cho hình bình hành và đường thẳng không có điểm chung với hình bình hành. Gọi là đường vuông góc kẻ từ đến đường thẳng Tìm mối liên hệ độ dài giữa
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
Lời giải:
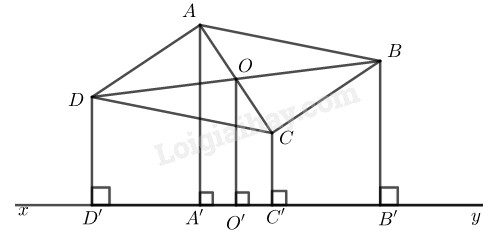
Gọi là giao điểm của và
Vì ABCD là hình bình hành nên (tính chất hình bình hành)
Kẻ
Suy ra:
Tứ giác là hình thang có: (chứng minh trên)
nên là trung điểm của
Suy ra là đường trung bình của hình thang
(tính chất đường trung bình của hình thang)
(theo cách vẽ)
Suy ra:
Tứ giác là hình thang có: (chứng minh trên)
nên là trung điểm của
Suy ra là đường trung bình của hình thang BDD’B’
(tính chất đường trung bình của hình thang)
Từ và suy ra:
Bài 87 Trang 90 SBT Toán 8 Tập 1 Cho hình bình hành có Ở phía ngoài hình bình hành, vẽ các tam giác đều
Tính
Chứng minh rằng tam giác là tam giác đều.
Phương pháp giải:
Sử dụng kiến thức:
+) Trong hình bình hành, hai góc kề một cạnh bù nhau.
+) Trong tam giác đều, các cạnh bằng nhau, các góc bằng nhau và bằng
+) Trong hình bình hành, hai góc đối bằng nhau.
+) Tam giác có cạnh bằng nhau là tam giác đều.
Lời giải:
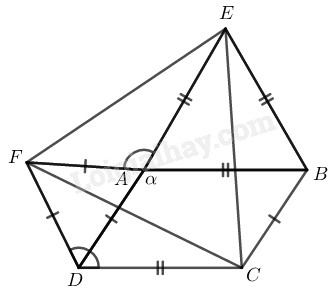
Vì
mà
( đều)
( đều)
nên
Vì ABCD là hình bình hành nên
Suy ra (hai góc trong cùng phía bù nhau)
Suy ra:
Tam giác ABE đều nên
Tam giác ADF đều nên
Vì ABCD là hình bình hành nên
Suy ra (vì cùng bằng ) và (vì cùng bằng )
Xét và
(vì đều)
(cmt)
(chứng minh trên)
Do đó
(tính chất hình bình hành)
Xét và
(cmt)
(cmt)
Do đó:
Từ và suy ra : Vậy đều.
Bài 88 Trang 90 SBT Toán 8 Tập 1 Cho tam giác Ở phía ngoài tam giác, vẽ các tam giác vuông cân tại là Vẽ hình bình hành Chứng minh rằng:
Phương pháp giải:
Quy về bài toán chứng minh hai tam giác bằng nhau.
Quy về chứng minh
+) Tổng ba góc trong một tam giác bằng
Lời giải:
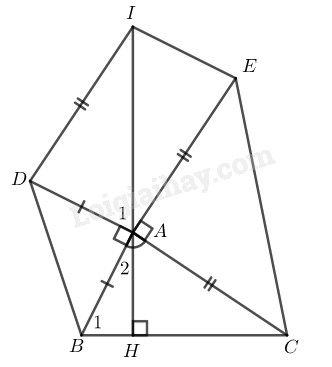
Suy ra:
Lại có (do ADIE là hình bình hành)
(hai góc trong cùng phía)
Từ và suy ra:
Xét và
(chứng minh trên)
(vì cùng bằng )
Do đó:
( chứng minh trên)
Gọi giao điểm và là
Ta có: (do H, A, I thẳng hàng)
mà
Từ và suy ra:
Trong ta có:
Suy ra hay
Bài 89 Trang 91 SBT Toán 8 Tập 1 Dựng hình bình hành biết:
a)
b) ( là giao điểm của hai đường chéo).
Phương pháp giải:
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài
Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện của đề bài.
Lời giải:
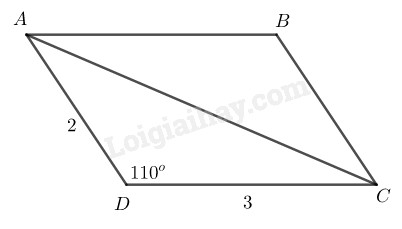
Cách dựng:
- Dựng có
- Dựng tia đi qua B và , dựng tia đi qua D và . Hai tia này cắt nhau tại
Ta có hình bình hành cần dựng
Chứng minh: nên tứ giác là hình bình hành.
Ta lại có Bài toán có một nghiệm hình.
b)
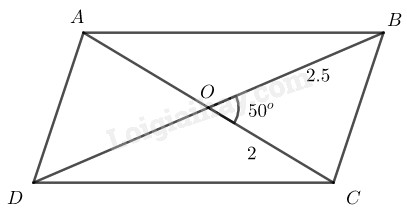
Cách dựng:
- Dựng có
- Trên tia đối tia lấy điểm sao cho
- Trên tia đối tia lấy điểm sao cho
Nối ta có hình bình hành cần dựng
Chứng minh: Tứ giác có nên nó là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Có
Bài toán có một nghiệm hình.
Bài 90 Trang 91 SBT Toán 8 Tập 1 Cho ba điểm trên giấy kẻ ô vuông Hãy vẽ điểm thứ tư sao cho là bốn đỉnh của một hình bình hành.

Phương pháp giải:
Dấu hiệu nhận biết:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tứ giác có các góc đối bằng nhau là hình bình hành.
Lời giải:
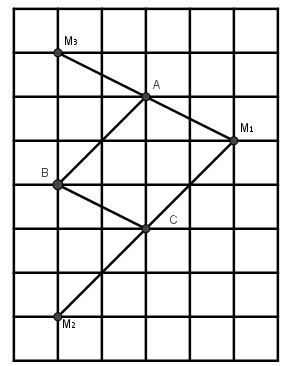
- Nếu hình bình hành nhận làm đường chéo vì là đường chéo hình vuông có cạnh là hai ô vuông nên là đường chéo hình vuông cạnh ô vuông và hai điểm nằm trên nửa mặt phẳng bờ ta có hình bình hành .
- Nếu hình bình hành nhận làm đường chéo, điểm cách điểm ba ô vuông , điểm cách là ba ô vuông và hai điểm cùng nằm trên nửa mặt phẳng bờ ta có hình bình hành
- Nếu hình bình hành nhận làm đường chéo thì điểm cách điểm ba ô vuông, hai điểm và nằm trên cùng một nửa mặt phẳng bờ ta có hình bình hành .
Bài 91 Trang 91 SBT Toán 8 Tập 1 Cho tam giác Dựng đường thẳng song song với cắt cạnh ở cắt cạnh ở sao cho
Phương pháp giải:
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đòng thời thể diện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
Lời giải:
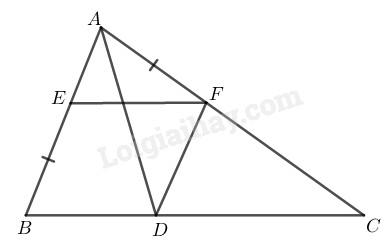
Cách dựng:
- Dựng đường phân giác của góc BAC.
- Qua dựng đường thẳng song song cắt tại
- Qua dựng đường thẳng song song với cắt tại
Ta có điểm cần dựng.
Chứng minh:
Vì
(so le trong)
(vì AD là tia phân giác của góc BAC)
Suy ra:
cân tại
Ta có: hay
hay
Suy ra tứ giác là hình bình hành (định nghĩa)
Từ và suy ra:
Bài 7.1 Trang 91 SBT Toán 8 Tập 1 Tứ giác là hình bình hành nếu:
và
và
Hãy chọn phương án đúng.
Phương pháp giải:
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Lời giải:
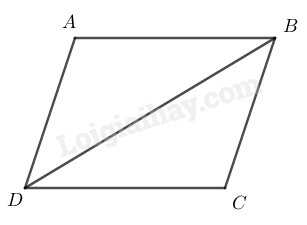
Chọn
Bài 7.2 Trang 91 SBT Toán 8 Tập 1 Cho hình bình hành các đường chéo cắt nhau tại Gọi theo thứ tự là trung điểm của Gọi là giao điểm của và Chứng minh rằng:
song song
Phương pháp giải:
Sử dụng kiến thức:
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
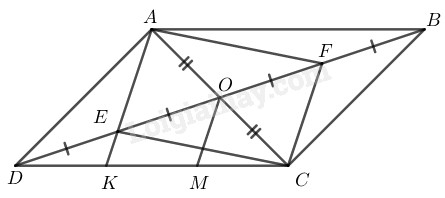
Vì ABCD là hình bình hành nên (tính chất hình bình hành)
(vì E là trung điểm của OD)
(vì F là trung điểm của OB)
Suy ra:
Xét tứ giác ta có:
(chứng minh trên)
(vì là hình bình hành)
Suy ra: Tứ giác là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường )
Kẻ
Trong ta có:
( chứng minh trên)
( theo cách vẽ)
(tính chất đường trung bình của tam giác)
Trong ta có:
(vì E là trung điểm của OD)
(do )
(tính chất đường trung bình của tam giác)
Từ và suy ra:
Bài 7.3 Trang 91 SBT Toán 8 Tập 1 Cho hình bình hành Lấy điểm trên cạnh điểm trên cạnh sao cho Chứng minh rằng ba đường thẳng đồng quy.
Phương pháp giải:
Sử dụng kiến thức:
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải:
Gọi là giao điểm của hai đường chéo và
Ta có (do ABCD là hình bình hành)
Xét tứ giác
(chứng minh trên)
Suy ra: Tứ giác là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
và cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm cạnh AC ( do ABCD là hình bình hành)
đi qua
Vậy đồng quy tại
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.