Toptailieu.vn giới thiệu Giải sách bài tập Toán lớp 8 Bài 9: Hình chữ nhật chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 9: Hình chữ nhật
Bài 106 Trang 93 SBT Toán 8 Tập 1 Cho tam giác đường trung tuyến và trọng tâm Gọi là điểm đối xứng với qua
Chứng minh rằng là điểm đối xứng với qua
Phương pháp giải:
Sử dụng kiến thức:
+) Ba đường trung tuyến trong tam giác cùng đi qua một điểm, điểm này cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến ứng với đỉnh đó.
+) Hai điểm gọi là đối xứng với nhau qua nếu là trung điểm của đoạn thẳng nối hai điểm đó.
Lời giải:
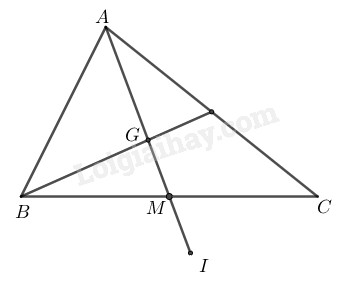
Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên thẳng hàng.
Vì đối xứng với qua tâm nên và thẳng hàng.
Lại có ( tính chất đường trung tuyến của tam giác)
Suy ra:
Mà:
Suy ra: nên điểm là trung điểm của
Vậy đối xứng với qua tâm
Bài 107 Trang 93 SBT Toán 8 Tập 1 Chứng minh rằng trong hình chữ nhật:
a) Giao điểm của hai đường chéo là tâm đối xứng của hình.
b) Hai đường thẳng đi qua trung điểm của hai cạnh đối là hai trục đối xứng của hình.
Phương pháp giải:
Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo
Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm của hai đáy.
Lời giải:
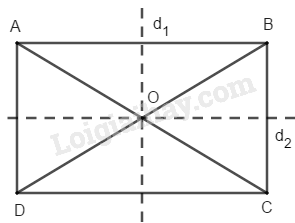
Gọi là giao điểm của hai đường chéo và
Vì hình chữ nhật là một hình bình hành nên điểm là tâm đối xứng của nó.
b) Ta biết trong hình thang cân đường thẳng đi qua trung điểm của hai đáy là trục đối xứng của nó.
Theo định nghĩa ta có hình chữ nhật cũng là một hình thang cân. Nếu ta xem hình chữ nhật là hình thang cân có hai cạnh đáy và thì đường thẳng đi qua trung điểm của và là trục đối xứng của hình chữ nhật
Nếu ta xem hình chữ nhật là hình thang cân có hai đáy là và nên đường thẳng đi qua trung điểm của và là trục đối xứng của hình chữ nhật
Bài 108 Trang 93 SBT Toán 8 Tập 1 Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng và (làm tròn kết quả đến chữ số thập phân thứ nhất)
Phương pháp giải:
Áp dụng định lí Py - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải:
Giả sử có , là trung điểm của Theo định lý Py-ta-go trong tam giác ABC vuông tại A, ta có:
Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên (tính chất tam giác vuông)
Bài 109 Trang 93 SBT Toán 8 Tập 1 Tính trên hình 16 (đơn vị đo : cm)
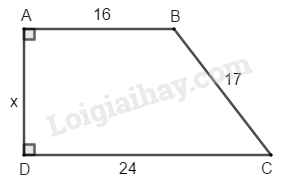
Phương pháp giải:
Áp dụng định lí Py - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải:
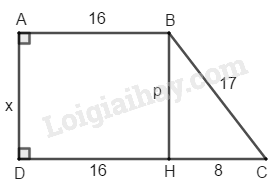
Kẻ
Suy ra: Tứ giác là hình chữ nhật (vì có ba góc vuông)
Suy ra
Trong tam giác vuông theo định lí Py-ta-go ta có:
Bài 110 Trang 93 SBT Toán 8 Tập 1 Chứng minh rằng các tia phân giác các góc của một hình bình hành cắt nhau tao thành một hình chữ nhật.
Phương pháp giải:
Sử dụng: Tổng ba góc trong tam giác bằng
Lời giải:
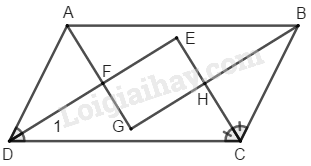
Giả sử ABCD là hình bình hành.
Gọi lần lượt là giao điểm của các đường phân giác của và ; và ; và ; và .
Ta có: (tính chất tia phân giác)
(tính chất tia phân giác)
(hai góc trong cùng phía)
Suy ra:
Trong ta có:
(đối đỉnh)
(hai góc trong cùng phía)
Trong ta có:
hay
(hai góc trong cùng phía)
Trong ta có: hay
Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).
Bài 111 Trang 94 SBT Toán 8 Tập 1
Tứ giác có hai đường chéo vuông góc với nhau. Gọi theo thứ tự là trung điểm các cạnh Tứ giác là hình gì ? Vì sao ?
Phương pháp giải:
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
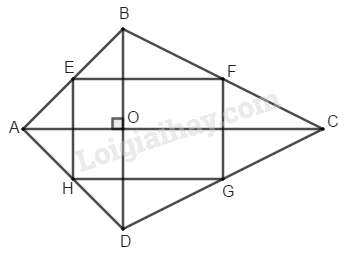
Trong ta có:
là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (1)
Trong ta có:
là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của
và (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: và
Suy ra: Tứ giác là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Ta lại có: (gt)
( chứng minh trên)
Suy ra:
Trong ta có là đường trung bình (vì E là trung điểm của AB và H là trung điểm của AD)
Suy ra: hay
Vậy hình bình hành là hình chữ nhật.
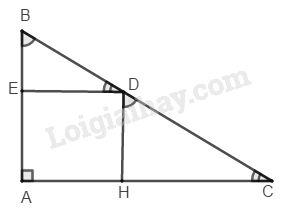
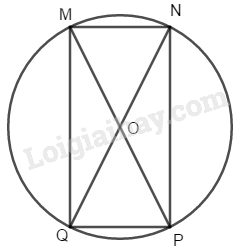
Bài 112 Trang 94 SBT Toán 8 Tập 1 Tìm các hình chữ nhật trên hình 17 (trong hình 17b, là tâm của đường tròn)
Phương pháp giải:
Áp dụng các tính chất của hình chữ nhật:
Hình bình hành có 1 góc vuông là hình chữ nhật
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau là hình chữ nhật.
Lời giải:
- Hình a ta có:
(vì có cặp góc đồng vị bằng nhau)
hay
(vì có cặp góc đồng vị bằng nhau)
hay
Suy ra tứ giác AHDE là hình bình hành ( có các cặp đối song song với nhau )
Mà
Nên tứ giác là hình chữ nhật.
- Hình b: Tứ giác có:
nên O là trung điểm của MP
nên O là trung điểm của NQ
Tứ giác MNPQ có O là trung điểm của mỗi đường chéo
Suy ra: Tứ giác MNPQ là hình bình hành
Lại có: ( = đường kính của đường tròn)
⇒ Tứ giác là hình chữ nhật.
Bài 113 Trang 94 SBT Toán 8 Tập 1 Các câu sau đúng hay sai ?
a) Hình chữ nhật là tứ giác có tất cả các góc bằng nhau.
b) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
c) Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
Phương pháp giải:
Áp dụng các tính chất của hình chữ nhật:
Hình tứ giác có ba góc vuông là hình chữ nhật
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau là hình chữ nhật.
Lời giải:
a) Đúng vì hình chữ nhật có góc vuông
b) Sai vì hình thang cân có hai cạnh bên không song song có hai đường chéo bằng nhau nhưng hình thang cân đó không là hình chữ nhật.
c) Đúng vì:
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Bài 114 Trang 94 SBT Toán 8 Tập 1 Cho tam giác vuông cân tại điểm thuộc cạnh Gọi theo thứ tự là chân các đường vuông góc kẻ từ đến
a) Tứ giác là hình gì ? Tính chu vi của tứ giác đó.
b) Điểm ở vị trí nào trên cạnh thì đoạn thẳng có độ dài nhỏ nhất ?
Phương pháp giải:
Áp dụng các tính chất sau:
Tứ giác có ba góc vuông là hình chữ nhật
Trong tam giác cân, đường cao ứng với cạnh đáy đồng thời là trung tuyến.
Lời giải:
a) Xét tứ giác ta có:
(gt)
(gt)
Lại có (gt)
Suy ra: Tứ giác là hình chữ nhật (vì có ba góc vuông)
vuông cân tại
Suy ra: vuông cân tại
Chu vi hình chữ nhật bằng :
b) Gọi là trung điểm của
Vì tam giác ABC cân tại A có AH là đường trung tuyến nên AH cũng là đường cao (tính chất tam giác cân)
Suy ra
Do đó, ( quan hệ đường vuông góc và đường xiên ) (dấu “=” xảy ra khi trùng với )
Tứ giác là hình chữ nhật
(tính chất hình chữ nhật)
Suy ra:
Vậy DE có độ dài nhỏ nhất là AH khi điểm là trung điểm của
Bài 115 Trang 94 SBT Toán 8 Tập 1 Cho tam giác cân tại các đường trung tuyến cắt nhau tại Gọi là điểm đối xứng với qua gọi là điểm đối xứng với qua Tứ giác là hình gì ? Vì sao ?
Phương pháp giải:
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
+) Tính chất đường trung tuyến: Cho , có là trung điểm , trọng tâm ta có
Lời giải:
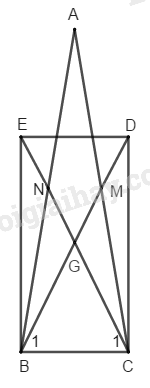
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: là trọng tâm của
(tính chất đường trung tuyến)
(tính chất đường trung tuyến)
Điểm đối xứng với điểm qua điểm
hay
Suy ra: (1)
Điểm đối xứng với điểm qua điểm
hay
Suy ra: (2)
Từ (1) và (2) suy ra tứ giác là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét và
cạnh chung
(tính chất tam giác cân ABC)
( vì )
Do đó:
cân tại
Hình bình hành có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Bài 116 Trang 94 SBT Toán 8 Tập 1 Cho hình chữ nhật Gọi là chân đường vuông góc kẻ từ đến Biết Tính các độ dài (làm tròn đến hàng đơn vị).
Phương pháp giải:
Tính chất hình chữ nhật: Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Định lý Py - ta - go trong tam giác ABC vuông tại A:
Lời giải:
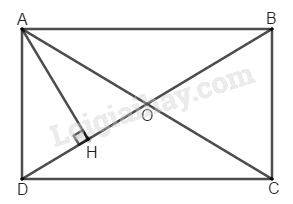
Ta có:
Vì ABCD là hình chữ nhật nên theo tính chất hình chữ nhật, ta có:
+
+
Lại có
Suy ra nên H là trung điểm của OD
Kết hợp với
Khi đó, tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên cân tại
Trong tam giác vuông có , ta có:
(định lý Py-ta-go)
Bài 117 Trang 94 SBT Toán 8 Tập 1 Chứng minh rằng ba điểm trên hình 18 thẳng hàng.
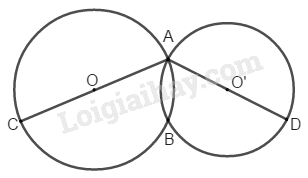
Phương pháp giải:
Sử dụng:
Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.
Lời giải:
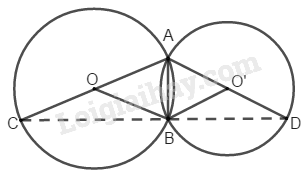
Nối
Trong ta có:
(bán kính đường tròn )
Nên là đường trung tuyến của
Mà (bán kính )
Nên tam giác vuông tại
Trong ta có: (bán kính )
Nên là đường trung tuyến của
Mà (bán kính )
Nên tam giác vuông tại
Vậy thẳng hàng.
Bài 118 Trang 94 SBT Toán 8 Tập 1 Tứ giác có Gọi theo thứ tự là trung điểm của Chứng minh rằng
Phương pháp giải:
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
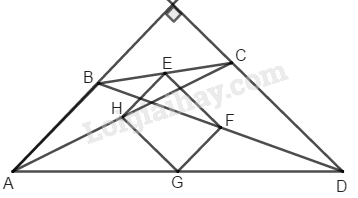
Trong ta có:
là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của
và (1)
Trong ta có:
là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của
và (2)
Từ (1) và (2) suy ra: và
Suy ra tứ giác là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Mặt khác: (chứng minh trên)
(gt)
Suy ra
Trong ta có là đường trung bình (do H là trung điểm của AC và E là trung điểm của BC)
Suy ra: hay
Vậy hình bình hành là hình chữ nhật.
Do đó (tính chất hình chữ nhật).
Bài 119 Trang 94 SBT Toán 8 Tập 1 Cho tam giác đường cao Gọi theo thứ tự là trung điểm của Chứng minh rằng tứ giác là hình thang cân.
Phương pháp giải:
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải:
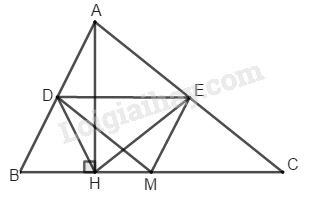
+ Vì là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của tam giác
hay
Suy ra: Tứ giác là hình thang
+ Vì là trung điểm của (gt)
là trung điểm của (gt)
nên là đường trung bình của
(tính chất đường trung bình của tam giác) (1)
Trong tam giác vuông có .
là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra:
Vậy hình thang là hình thang cân (vì có hai đường chéo bằng nhau
Bài 120 Trang 95 SBT Toán 8 Tập 1 Cho tam giác vuông tại điểm thuộc cạnh . Gọi theo thứ tự là trung điểm của Chứng minh rằng tứ giác là hình thang cân.
Phương pháp giải:
Áp dụng tính chất đường trung bình của tam giác
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Định nghĩa hình thang cân: Hình thang có hai góc ở đáy bằng nhau là hình thang cân.
Lời giải:
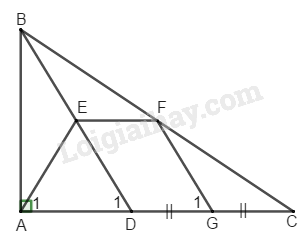
Trong ta có:
là trung điểm của (gt)
là trung điểm của (gt)
Nên là đường trung bình của
hay
Suy ra: Tứ giác là hình thang
+ Vì là trung điểm của (gt)
là trung điểm của (gt)
Nên là đường trung bình của
(đồng vị) (1)
Trong tam giác vuông tại có là trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
Nên cân tại (2)
Từ (1) và (2) suy ra:
Vậy hình thang là hình thang cân (theo định nghĩa).
Bài 121 Trang 95 SBT Toán 8 Tập 1 Cho tam giác nhọn các đường cao Gọi theo thứ tự là chân các đường vuông góc kẻ từ đến đường thẳng Chứng minh rằng
HD: Vẽ điểm là trung điểm của điểm là trung điểm của
Phương pháp giải:
Áp dụng tính chất đường trung bình của tam giác
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Lời giải:
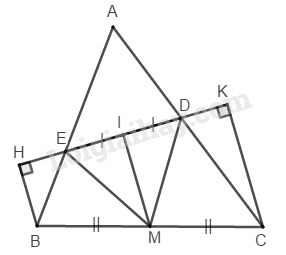
Ta có: (gt)
(gt)
Suy ra nên tứ giác là hình thang
Ta có: Gọi là trung điểm của là trung điểm của
Trong tam giác vuông tại có là trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
Trong tam giác vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
Suy ra: nên cân tại
cân tại có là đường trung tuyến nên là đường cao
Suy ra: (cùng vuông góc với DE)
Xét hình thang có và
Suy ra: (tính chất đường trung bình hình thang)
mà ( theo cách vẽ)
Bài 122 Trang 95 SBT Toán 8 Tập 1 Cho tam giác vuông tại đường cao Gọi theo thứ tự là chân các đường vuông góc kẻ từ đến
a. Chứng minh rằng
b. Gọi là trung điểm của là trung điểm của Chứng minh rằng
Phương pháp giải:
Hình tứ giác có ba góc vuông là hình chữ nhật
Hình chữ nhật có hai đường chéo bằng nhau.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Lời giải:
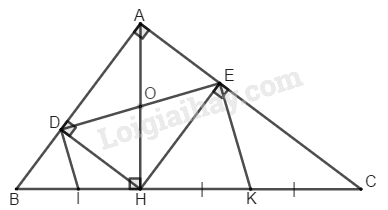
a. Xét tứ giác
(gt)
(vì )
(vì )
Suy ra tứ giác là hình chữ nhật (vì có ba góc vuông)
(tính chất hình chữ nhật)
b. vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
cân tại (1)
vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
cân tại (2)
Tứ giác là hình chữ nhật
hay
(hai góc đồng vị) (3)
Từ (1), (2) và (3) suy ra:
Mà 2 góc này ở vị trí đồng vị
Bài 123 Trang 95 SBT Toán 8 Tập 1 Cho tam giác vuông tại A, đường cao AH, đường trung tuyến AM.
a. Chứng minh rằng
b. Gọi theo thứ tự là chân các đường vuông góc kẻ từ đến Chứng minh rằng AM vuông góc với DE.
Phương pháp giải:
Hình tứ giác có ba góc vuông là hình chữ nhật.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Lời giải:
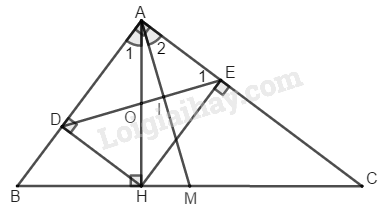
a. (gt)
(vì ∆ ABC có )
Suy ra: (1)
vuông tại có là trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
cân tại (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra:
b. xét tứ giác ADHE có:
(gt)
(vì )
(vì )
Suy ra: Tứ giác là hình chữ nhật (vì có ba góc vuông)
+ Xét và có :
DH chung
( vì ADHE là hình chữ nhật)
( vì ADHE là hình chữ nhật)
Lại có:
Suy ra:
(chứng minh câu a)
Gọi là giao điểm của và
Trong ta có:
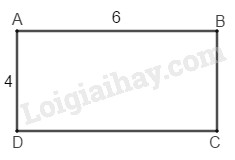
Bài 9.1 Trang 95 SBT Toán 8 Tập 1 Một hình chữ nhật có hai cạnh kề bằng và Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?
A.
B.
C.
D.
Hãy chọn phương án đúng.
Phương pháp giải:
Áp dụng định lí Py - ta - go trong tam giác ABD vuông tại A:
Lời giải:
Chọn B.
Theo định lý Pytago ta có:
Nên độ dài đường chéo hình chữ nhật là:
Bài 9.2 Trang 95 SBT Toán 8 Tập 1 Cho tam giác vuông tại đường cao Gọi theo thứ tự là trung điểm của Tính số đo góc
Phương pháp giải:
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải:
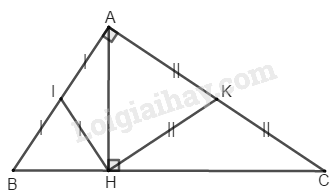
vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
cân tại
(1)
vuông tại có là đường trung tuyến ứng với cạnh huyền
(tính chất tam giác vuông)
cân tại (2)
(3)
Từ (1), (2) và (3) suy ra: .
Bài 9.3 Trang 95 SBT Toán 8 Tập 1 Cho hình thang cân đường cao Gọi theo thứ tự là trung điểm của các cạnh bên Chứng minh rằng là hình bình hành.
Phương pháp giải:
Tính chất đường trung bình của hình thang
Tính chất tam giác vuông (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Lời giải:
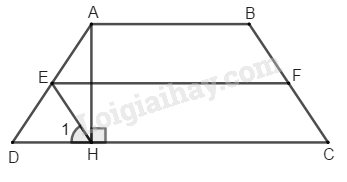
Ta có: là trung điểm của (gt)
là trung điểm của (gt)
Nên là đường trung bình của hình thang
hay (*)
vuông tại có là đường trung tuyến ứng với cạnh huyền
Ta có: (tính chất tam giác vuông)
cân tại
(tính chất tam giác cân)
(vì ABCD là hình thang cân)
Suy ra:
(**) (vì có cặp góc đồng vị bằng nhau)
Từ (*) và (**) suy ra tứ giác là hình bình hành (1 cặp cạnh song song và bằng nhau).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.