Toptailieu.vn xin giới thiệu Lý thuyết Giá trị lượng giác của một góc lượng giác (Chân trời sáng tạo) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:

Lý thuyết Giá trị lượng giác của một góc lượng giác (Chân trời sáng tạo) hay, chi tiết | Lý thuyết Toán 11

A. Lý thuyết Giá trị lượng giác của một góc lượng giác

1. Giá trị lượng giác của góc lượng giác

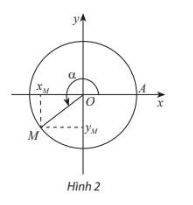
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó

$x=$cos$\alpha$, $y=$sin$\alpha$.

tan$\alpha$$=\frac{\sin \alpha }{\cos \alpha }=\frac{y}{x}\left(x\ne 0\right)$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x}{y}\left(y\ne 0\right)$

- Các giá trị sin$\alpha$, cos$\alpha$, tan$\alpha$, cot$\alpha$ được gọi là các giá trị lượng giác của góc lượng giác $\alpha$.

*Chú ý:

a, Trục tung là trục sin, trục hoành là trục côsin.

Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang

Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.

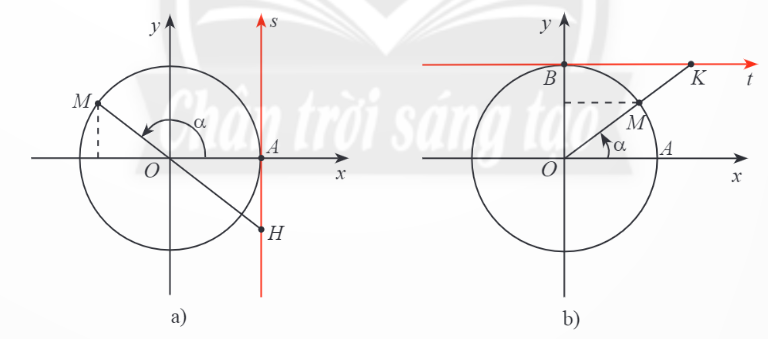
b, sin a và cos a xác định với mọi a thuộc R

$\tan \alpha$xác định với các góc  $\alpha \ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

$\cot \alpha$ xác định với các góc  $\alpha \ne k\pi ,k\in \mathbb{Z}$.

c, Với mọi góc lượng giác $\alpha$ và số nguyên k, ta có:

$\begin{array}{l}\sin \left(\alpha +k2\pi \right)=\sin \alpha \\ \cos \left(\alpha +k2\pi \right)=\cos \alpha \\ \tan \left(\alpha +k\pi \right)=\tan \alpha \\ \cot \left(\alpha +k\pi \right)=\cot \alpha \end{array}$

d, Bảng các giá trị lượng giác đặc biệt

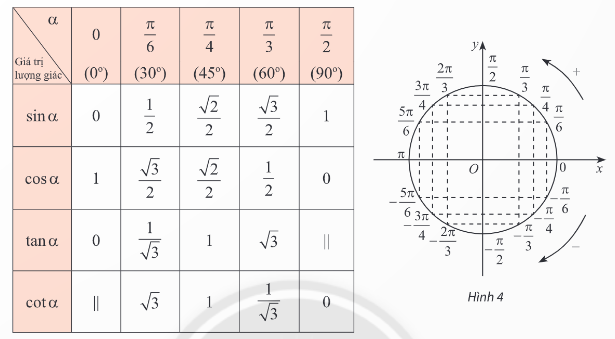
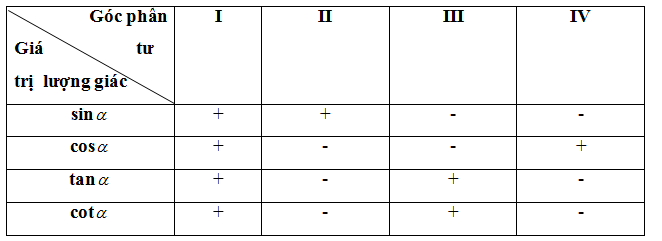
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay

- Lần lượt ấn các phím SHIFT -> MENU -> 2:

Để chọn đơn vị độ: ấn phím 1 (Degree).

Để chọn đơn vị radian: ấn phím 2 (Radian).

- Ấn các phím MENU 1 để vào chế độ tính toán.

3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

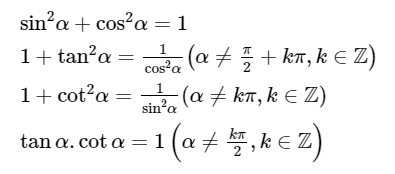
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt 

Hai góc đối nhau $\alpha$và $-\alpha$

$\begin{array}{l}\sin \left(-\alpha \right)=-\sin \alpha \\ \cos \left(-\alpha \right)=\cos \alpha \\ \tan \left(-\alpha \right)=-\tan \alpha \\ \cot \left(-\alpha \right)=-\cot \alpha \end{array}$

Hai góc bù nhau ($\alpha$và $\pi$-$\alpha$)

$\begin{array}{l}\sin \left(\pi -\alpha \right)=\sin \alpha \\ \cos \left(\pi -\alpha \right)=-\cos \alpha \\ \tan \left(\pi -\alpha \right)=-\tan \alpha \\ \cot \left(\pi -\alpha \right)=-\cot \alpha \end{array}$

Hai góc phụ nhau ($\alpha$và $\frac{\pi }{2}$-$\alpha$)

$\begin{array}{l}\sin \left(\frac{\pi }{2}-\alpha \right)=c\mathrm{o}\mathrm{s}\alpha \\ \cos \left(\frac{\pi }{2}-\alpha \right)=\sin \alpha \\ \tan \left(\frac{\pi }{2}-\alpha \right)=\cot \alpha \\ \cot \left(\frac{\pi }{2}-\alpha \right)=\tan \alpha \end{array}$

Hai góc hơn kém $\pi$(và $\pi$+$\alpha$)

$\begin{array}{l}\sin \left(\pi +\alpha \right)=-\sin \alpha \\ \cos \left(\pi +\alpha \right)=-\cos \alpha \\ \tan \left(\pi +\alpha \right)=\tan \alpha \\ \cot \left(\pi +\alpha \right)=\cot \alpha \end{array}$

B. Bài tập Giá trị lượng giác của một góc lượng giác

Bài 1. Rút gọn các biểu thức sau:

a) A = (1 – sin²α).cot²α + 1 – cot²α;

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$.

Hướng dẫn giải

a) A = (1 – sin²α).cot²α + 1 – cot²α

⇔ A = cot²α – sin²α.cot²α + 1 – cot²α

⇔ $A=1-{\sin }^2\alpha .\frac{{\cos }^2\alpha }{{\sin }^2\alpha }={\sin }^2\alpha .$

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$

⇔ $B=\frac{{\cos }^2\alpha -{\sin }^2\alpha }{\sin \alpha +\cos \alpha }$

⇔ B = cos α – sin α.

Bài 2. Cho $\tan \alpha =\frac{3}{5}.$ Tính: $A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }.$

Hướng dẫn giải

Chia cả tử và mẫu của biểu thức A cho cos²α ta được:

$A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }=\frac{\tan \alpha }{{\tan }^2\alpha -1}=-\frac{15}{16}.$

Bài 3. Tính các giá trị lượng giác của góc α biết:

a) $\tan \alpha =-\frac{4}{5}$ biết $\frac{3\pi }{2}<\alpha <2\pi .$

b) $\cot \alpha =-\frac{19}{7}$ biết $\frac{\pi }{2}<\alpha <\pi .$

Hướng dẫn giải

a) Do $\frac{3\pi }{2}<\alpha <2\pi$ nên sin α < 0, cos α > 0, cot α < 0.

Ta có:

$\cot \alpha =\frac{1}{\tan \alpha }\Rightarrow \cot \alpha =-\frac{5}{4}.$

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }\Rightarrow \sin \alpha =\tan \alpha .\cos \alpha =-\frac{4}{5}.\frac{5}{\sqrt{41}}=-\frac{4\sqrt{41}}{41}.$

b) Do $\frac{\pi }{2}<\alpha <\pi$ nên sin α > 0, cos α < 0, tan α < 0.

Ta có:

$\tan \alpha =\frac{1}{\cot \alpha }\Rightarrow \tan \alpha =-\frac{7}{19}.$

Mà cos α < 0 ⇒ $\cos \alpha =-\frac{19}{\sqrt{410}}.$

Xem thêm Lý thuyết các bài  Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Góc lượng giác

Lý thuyết Bài 3: Các công thức lượng giác

Lý thuyết Bài 4: Hàm số lượng giác và đồ thị

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số