Toptailieu.vn biên soạn và giới thiệu lời giải Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 5: Phép quay hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Chuyên đề Toán 11 Bài 5 từ đó học tốt môn Toán 11.

Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 5: Phép quay

Khởi động trang 25 Chuyên đề Toán 11: Vẽ mỗi hình sau ra một tờ giấy, cắt rời mỗi hình theo hình tròn. Tìm một điểm O trên mỗi hình. Sau đó, ghim hình đã cắt được xuống mặt bàn tại điểm O, thử xoay hình một góc φ nào đó. Có nhận xét gì về kích thước của hình trước khi xoay và sau khi xoay?

Lời giải:

Giả sử chọn điểm O trên mỗi hình như hình vẽ dưới đây.

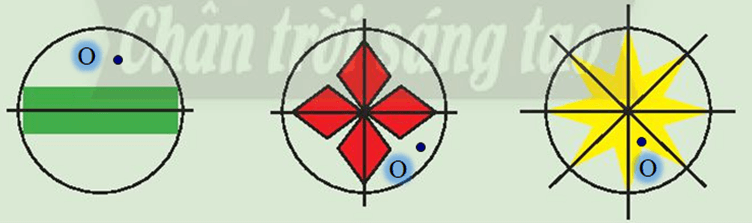
Trong cả 3 hình đã cho, kích thước của hình trước khi xoay và sau khi xoay không thay đổi.

1. Định nghĩa

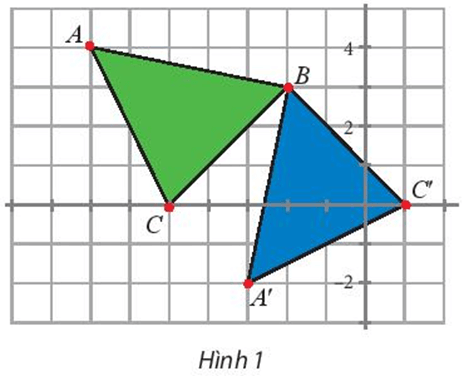
Khám phá 1 trang 25 Chuyên đề Toán 11: a) Tìm phép biến hình biến ∆BAC thành ∆BA’C’ (Hình 1).

b) Trong mặt phẳng, cho điểm O cố định (Hình 2).

Gọi f là quy tắc ứng với mỗi điểm M trùng O cho ta điểm O và ứng với điểm M khác O cho ta một điểm M’ xác định như sau:

– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.

– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng 60°.

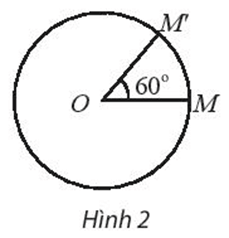
Quy tắc f có phải là một phép biến hình không?

Hãy vẽ điểm M’ theo quy tắc trên nếu thay góc 60° bởi góc –30°.

Lời giải:

a) Để tìm phép biến hình biến ∆BAC thành ∆BA’C’, ta tìm phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’, biến điểm C thành điểm C’.

Với A(–7; 4), B(–2; 3), C(–5; 0), A’(–3; –2), C’(1; 0), ta có:

$\overrightarrow{\mathrm{BA}}=\left(-5;1\right),\overrightarrow{{\mathrm{BA}}^{\text{'}}}=\left(-1;-5\right),\overrightarrow{{\mathrm{AA}}^{\text{'}}}=\left(4;-6\right)$.

Suy ra $\mathrm{BA}={\mathrm{BA}}^{\text{'}}=\sqrt{26}$ và ${\mathrm{AA}}^{\text{'}}=2\sqrt{13}$.

Khi đó $\cos \widehat{{\mathrm{ABA}}^{\text{'}}}=\frac{{\mathrm{BA}}^2+B{A^{\text{'}}}^2-A{A^{\text{'}}}^2}{2.\mathrm{BA}.{\mathrm{BA}}^{\text{'}}}=\frac{26+26-{\left(2\sqrt{13}\right)}^2}{2.\sqrt{26}.\sqrt{26}}=0$.

Vì vậy $\left(\mathrm{BA},{\mathrm{BA}}^{\text{'}}\right)=\widehat{{\mathrm{ABA}}^{\text{'}}}=90°$.

Suy ra phép biến hình biến đoạn thẳng BA thành đoạn thẳng BA’ là phép biến hình biến điểm B thành điểm B, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác (BA, BA’) = 90° (1)

Thực hiện tương tự, ta được $\mathrm{BC}={\mathrm{BC}}^{\text{'}}=3\sqrt{2}$ và $\left(\mathrm{BC},{\mathrm{BC}}^{\text{'}}\right)=90°$.

Suy ra phép biến hình biến đoạn thẳng BC thành đoạn thẳng BC’ là phép biến hình biến điểm B thành điểm B, biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác (BC, BC’) = 90° (2)

Từ (1), (2), ta thu được phép biến hình biến ∆BAC thành ∆BA’C’ là phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác (BA, BA’) = 90° và biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác (BC, BC’) = 90°.

b) Đặt f(M) = M’. Trong đó, M’ là điểm nằm trên (C) sao cho góc lượng giác (OM, OM’) bằng 60°.

Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.

Vậy f là một phép biến hình.

Cách vẽ điểm M’ theo quy tắc trên với góc lượng giác (OM, OM’) bằng –30°:

– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.

– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng –30°.

Ta có hình vẽ sau:

Thực hành 1 trang 26 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ lần lượt qua các phép quay Q_{(O, 45°)}, Q_{(O, 90°)}, Q_{(O, 180°)}, Q_{(O, 360°)}.

Lời giải:

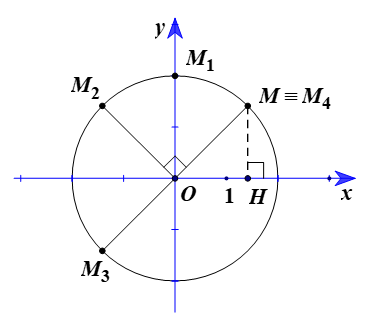
Ta có $\overrightarrow{\mathrm{OM}}=\left(\sqrt{2};\sqrt{2}\right)$. Suy ra OM = 2.

Vẽ đường tròn (C) tâm O bán kính OM.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 45°)}:

Ta có Q_{(O, 45°)} biến điểm M khác O thành điểm M₁ sao cho OM₁ = OM = 2 và (OM, OM₁) = 45° nên $\widehat{{\mathrm{MOM}}_1}=45°$.

Kẻ MH ⊥ Ox tại H.

Tam giác OMH vuông tại H: $\cos \widehat{\mathrm{MOH}}=\frac{\mathrm{OH}}{\mathrm{OM}}=\frac{\sqrt{2}}{2}$.

Suy ra $\widehat{\mathrm{MOH}}=45°$.

Ta có $\widehat{{\mathrm{HOM}}_1}=\widehat{\mathrm{HOM}}+\widehat{{\mathrm{MOM}}_1}=45°+45°=90°$.

Suy ra M₁ ∈ Oy nên $x_{M_1}=0$.

Mà OM₁ = 2 (chứng minh trên) nên .

Vậy tọa độ M₁(0; 2).

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 90°)}:

Ta có Q_{(O, 90°)} biến điểm M khác O thành điểm M₂ sao cho OM₂ = OM = 2 và (OM, OM₂) = 90° nên $\widehat{{\mathrm{MOM}}_2}=90°$.

Suy ra tam giác MOM₂ vuông cân tại O.

Ta có $\widehat{M_1{\mathrm{OM}}_2}=\widehat{{\mathrm{MOM}}_2}-\widehat{{\mathrm{MOM}}_1}=90°-45°=45°$.

Suy ra $\widehat{{\mathrm{MOM}}_1}=\widehat{M_1{\mathrm{OM}}_2}=45°$.

Khi đó tam giác MOM₂ có OM₁ là đường phân giác.

Vì vậy OM₁ cũng là đường trung trực của tam giác MOM₂ hay Oy là đường trung trực của tam giác MOM₂.

Suy ra M₂ là ảnh của điểm M qua phép đối xứng trục Oy.

Do đó hai điểm $M\left(\sqrt{2};\sqrt{2}\right)$ và M₂ có cùng tung độ và có hoành độ đối nhau.

Vậy tọa độ $M_2\left(-\sqrt{2};\sqrt{2}\right)$.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 180°)}:

Ta có Q_{(O, 180°)} biến điểm M khác O thành điểm M₃ sao cho OM₃ = OM = 2 và (OM, OM₃) = 180° nên $\widehat{{\mathrm{MOM}}_3}=180°$.

Suy ra O là trung điểm của MM₃.

Khi đó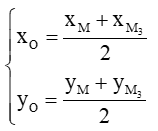 

Vì vậy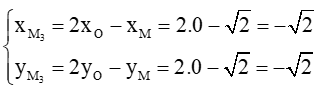 

Vậy tọa độ $M_3\left(-\sqrt{2};-\sqrt{2}\right)$.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 360°)}:

Ta có Q_{(O, 360°)} biến điểm M khác O thành điểm M₄ sao cho OM₄ = OM = 2 và (OM, OM₄) = 360° nên $\widehat{{\mathrm{MOM}}_4}=360°$.

Tức là, M₄ ≡ M.

Vậy tọa độ $M_4\left(\sqrt{2};\sqrt{2}\right)$.

Vận dụng 1 trang 27 Chuyên đề Toán 11: Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:

a) rẽ sang hướng tây?

b) rẽ sang hướng đông?

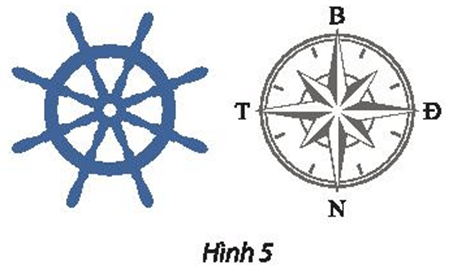
Lời giải:

a) Để con tàu rẽ sang hướng tây, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = 90°.

b) Để con tàu rẽ sang hướng đông, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = –90°.

2. Tính chất

Khám phá 2 trang 27 Chuyên đề Toán 11: Cho phép quay Q_{(O; φ)} và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?

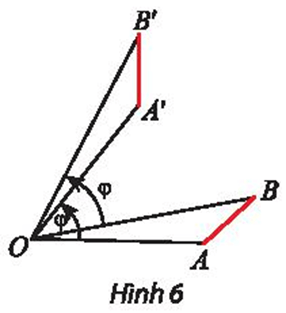
Lời giải:

Ta có Q_{(O, φ)} biến điểm A khác O thành điểm A’ sao cho OA = OA’ và (OA, OA’) = φ nên $\widehat{{\mathrm{AOA}}^{\text{'}}}=\phi$.

Tương tự, ta có Q_{(O, φ)} biến điểm B khác O thành điểm B’ sao cho OB = OB’ và (OB, OB’) = φ nên $\widehat{{\mathrm{BOB}}^{\text{'}}}=\phi$.

Ta có $\widehat{{\mathrm{AOA}}^{\text{'}}}=\widehat{{\mathrm{BOB}}^{\text{'}}}\left(=\phi \right)$.

Suy ra $\widehat{\mathrm{AOB}}+\widehat{{\mathrm{BOA}}^{\text{'}}}=\widehat{{\mathrm{BOA}}^{\text{'}}}+\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}$.

Do đó $\widehat{\mathrm{AOB}}=\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}$.

Xét ∆OAB và ∆OA’B’, có:

OA = OA’ (chứng minh trên);

OB = OB’ (chứng minh trên);

$\widehat{\mathrm{AOB}}=\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}$ (chứng minh trên).

Vậy ∆OAB = ∆OA’B’ (c.g.c).

Thực hành 2 trang 28 Chuyên đề Toán 11: Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay Q_{(I, 90°)} của các hình sau:

a) Tam giác IAB;

b) Đường thẳng BC;

c) Đường tròn (B, a).

Lời giải:

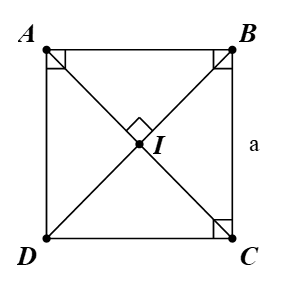
a) Hình vuông ABCD có tâm I.

Suy ra AC ⊥ BD tại I và IA = IB = IC = ID.

Ta có phép quay Q_{(I, 90°)} biến:

⦁ Điểm I thành điểm I.

⦁ Điểm A thành điểm D;

⦁ Điểm B thành điểm A;

Vậy ảnh của tam giác IAB qua phép quay Q_{(I, 90°)} là tam giác IDA.

b) Ta có phép quay Q_{(I, 90°)} biến:

⦁ Điểm B thành điểm A;

⦁ Điểm C thành điểm B.

Vậy ảnh của đường thẳng BC qua phép quay Q_{(I, 90°)} là đường thẳng AB.

c) Ta có phép quay Q_{(I, 90°)} biến điểm B thành điểm A.

Vậy ảnh của đường tròn (B, a) qua phép quay Q_{(I, 90°)} là đường tròn (A, a).

Vận dụng 2 trang 28 Chuyên đề Toán 11: Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay Q_{(O, φ)} biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.

Lời giải:

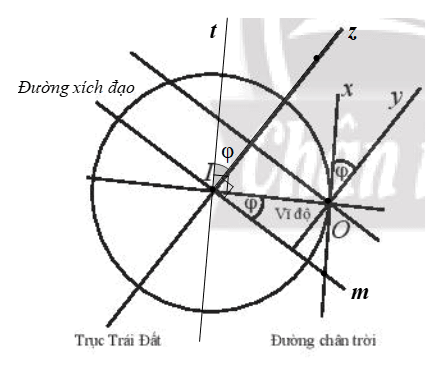
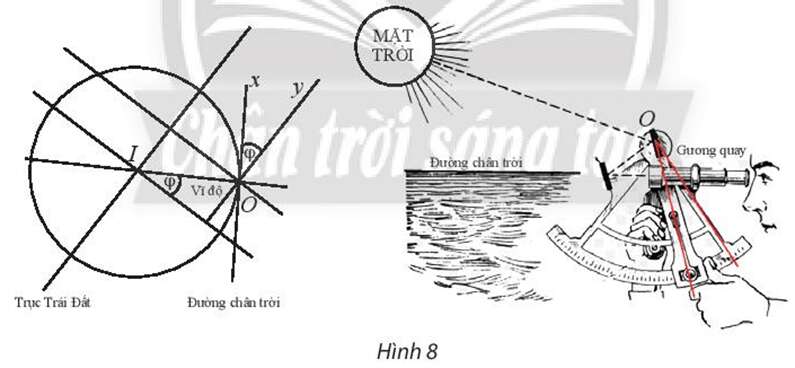
Gọi Iz là tia trùng với trục Trái Đất và nằm trên cùng một nửa mặt phẳng bờ IO chứa tia Ox, Oy.

Kẻ tia It song song với tia Ox.

Mà tia Oy song song với trục Trái Đất (giả thiết).

Do đó $\widehat{\mathrm{tIz}}=\widehat{\mathrm{xOy}}=\phi$.

Ta có tia Ox tiếp xúc với Trái Đất tại O.

Suy ra Ox là tiếp tuyến của đường tròn (I, IO).

Do đó Ox ⊥ IO.

Mà Ox // Ot nên Ot ⊥ IO.

Khi đó $\widehat{\mathrm{tIz}}+\widehat{\mathrm{zIO}}=90°$ (1)

Gọi Im là tia trùng với đường xích đạo và nằm trên cùng một nửa mặt phẳng bờ Iz chứa đoạn thẳng IO.

Vì trục Trái Đất vuông góc với đường xích đạo nên ta có Iz ⊥ Im.

Suy ra $\widehat{\mathrm{mIO}}+\widehat{\mathrm{zIO}}=90°$ (2)

Từ (1), (2), ta có $\widehat{\mathrm{mIO}}=\widehat{\mathrm{tIz}}=\phi$.

Vậy góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.

Bài tập

Bài 1 trang 28 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3).

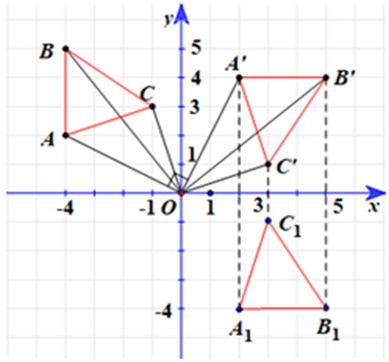
a) Chứng minh các điểm A’(2; 4), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.

b) Gọi ∆A₁B₁C₁ là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của ∆A₁B₁C₁.

Lời giải:

a)

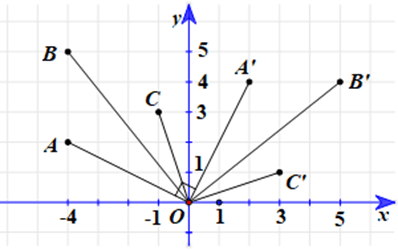
Với A(–4; 2) và A’(2; 4), ta có $\overrightarrow{\mathrm{OA}}=\left(-4;2\right),\overrightarrow{{\mathrm{OA}}^{\text{'}}}=\left(2;4\right),\overrightarrow{{\mathrm{AA}}^{\text{'}}}=\left(6;2\right)$.

Do đó $\mathrm{OA}={\mathrm{OA}}^{\text{'}}=2\sqrt{5}$ và ${\mathrm{AA}}^{\text{'}}=2\sqrt{10}$.

Suy ra $\cos \widehat{{\mathrm{AOA}}^{\text{'}}}=\frac{{\mathrm{OA}}^2+O{A^{\text{'}}}^2-A{A^{\text{'}}}^2}{2.\mathrm{OA}.{\mathrm{OA}}^{\text{'}}}=\frac{{\left(2\sqrt{5}\right)}^2+{\left(2\sqrt{5}\right)}^2-{\left(2\sqrt{10}\right)}^2}{2.2\sqrt{5}.2\sqrt{5}}=0$.

Do đó $\widehat{{\mathrm{AOA}}^{\text{'}}}=90°$.

Mà khi quay đoạn OA (với tâm O) theo hướng cùng chiều kim đồng hồ một góc 90° thì ta được đoạn OA’. Tức là, phép quay có góc quay lượng giác theo chiều âm một góc 90°.

Vì vậy góc lượng giác (OA, OA’) = –90°.

Vậy A’ là ảnh của A qua phép quay tâm O với góc quay –90°.

Chứng minh tương tự, ta thu được B’, C’ theo thứ tự là ảnh của B, C qua phép quay tâm O với góc quay –90°.

b) Từ câu a, ta có phép quay tâm O, góc quay –90° biến ∆ABC thành ∆A’B’C’.

Ta có: ∆A₁B₁C₁ là ảnh của ∆A’B’C’ qua phép đối xứng trục Ox nên:

• A₁ = Đ_Ox(A’), do đó hai điểm A₁­ và A’(2; 4) có cùng hoành độ và có tung độ đối nhau, suy ra A₁(2; –4).

• B₁ = Đ_Ox(B’), do đó hai điểm B₁­ và B’(5; 4) có cùng hoành độ và có tung độ đối nhau, suy ra B₁(5; –4).

• C₁ = Đ_Ox(C’), do đó hai điểm C₁­ và C’(3; 1) có cùng hoành độ và có tung độ đối nhau, suy ra C₁(3; –1).

Vậy tọa độ các đỉnh của ∆A₁B₁C₁ thỏa mãn yêu cầu bài toán là A₁(2; –4), B₁(5; –4), C₁(3; –1).

Bài 2 trang 29 Chuyên đề Toán 11: Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.

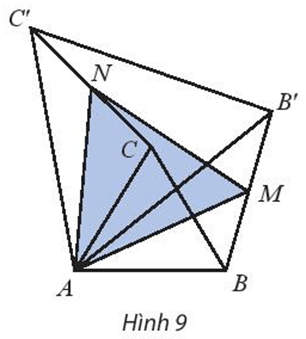
Lời giải:

Do DABC là tam giác đều nên AB = AC và $\widehat{\mathrm{BAC}}=60°$

Do DAB’C’ là tam giác đều nên AB’ = AC’ và $\widehat{{\mathrm{B}}^{\text{'}}{\mathrm{AC}}^{\text{'}}}=60°$

Ta có phép quay tâm A, góc quay 60° biến:

⦁ Điểm B thành điểm C;

⦁ Điểm B’ thành điểm C’.

Do đó ảnh của đoạn thẳng BB’ qua phép quay tâm A, góc quay 60° là đoạn thẳng CC’.

Mà M, N lần lượt là trung điểm của BB’, CC’ (giả thiết).

Do đó phép quay tâm A, góc quay 60° biến điểm M thành điểm N.

Suy ra AM = AN và $\widehat{\mathrm{MAN}}=\left(\mathrm{AM},\mathrm{AN}\right)=60°$

DAMN có AM = AN và $\widehat{\mathrm{MAN}}=60°$ nên là tam giác đều.

Vậy ∆AMN đều.

Bài 3 trang 29 Chuyên đề Toán 11: Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC, CD, DA, KF, HC, HL. Chứng minh hình thang AEJK và hình thang FLIC bằng nhau.

Lời giải:

Nội dung đang được cập nhật

Bài 4 trang 29 Chuyên đề Toán 11: Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.

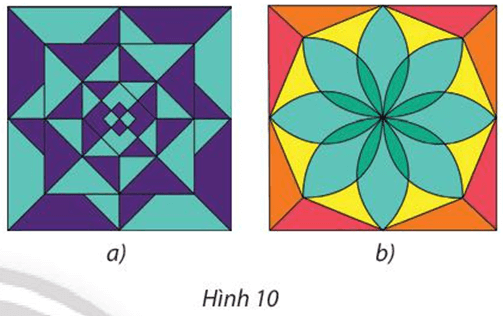
Lời giải:

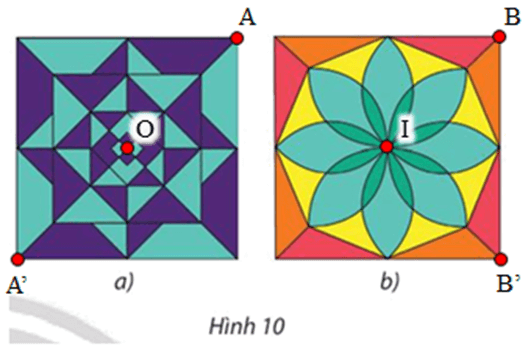
⦁ Hình 10a:

Hình vẽ có dạng hình vuông, gọi O là tâm hình vuông đó và A là 1 đỉnh của hình vuông.

Phép quay tâm O, góc quay 180° biến điểm A thành điểm A’.

Tương tự, ta chọn các điểm khác bất kì trên Hình 10a.

Khi đó qua phép quay tâm O, góc quay 180° ta cũng xác định được ảnh của các điểm đó trên Hình 10a ban đầu.

Vậy phép quay biến Hình 10a thành chính nó là phép quay tâm O, góc quay 180°.

Ngoài ra, phép quay tâm O, góc quay –180° cũng biến Hình 10a thành chính nó.

⦁ Hình 10b:

Hình vẽ có dạng hình vuông, gọi I là tâm hình vuông đó và B là 1 đỉnh của hình vuông.

Phép quay tâm I, góc quay 90° biến điểm B thành điểm B’.

Tương tự, ta chọn các điểm khác bất kì trên hình 10b.

Khi đó qua phép quay tâm I, góc quay 90° ta cũng xác định được ảnh của các điểm đó trên Hình 10b ban đầu.

Vậy phép quay biến Hình 10b thành chính nó là phép quay tâm I, góc quay 90°.

Chú ý: Có nhiều phép quay biến Hình 10a thành chính nó, chẳng hạn ngoài phép quay ở trên, ta có thể kể đến phép quay tâm I, góc quay 180° hoặc phép quay tâm I, góc quay –90°, …

Bài 5 trang 29 Chuyên đề Toán 11: Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của ∆OAA’ và ∆OBB’. Chứng minh rằng ∆OGG’ là tam giác vuông cân.

Lời giải:

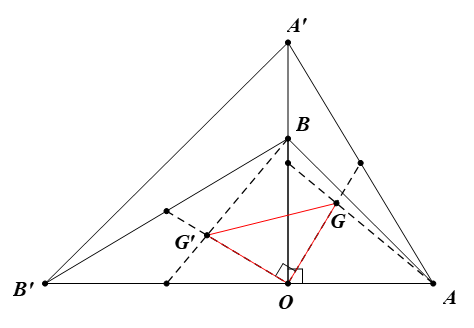
Do DOAB là tam giác vuông cân nên OA = OB và $\widehat{\mathrm{AOB}}=90°$.

Do DOA’B’ là tam giác vuông cân nên OA’ = OB’ và $\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}=90°$.

Phép quay tâm O, góc quay 90° biến:

⦁ Điểm O thành điểm O;

⦁ Điểm A thành điểm B;

⦁ Điểm A’ thành điểm B’.

Do đó ảnh của ∆OAA’ qua phép quay tâm O, góc quay 90° là ∆OBB’.

Mà G, G’ lần lượt là trọng tâm của ∆OAA’ và ∆OBB’.

Vì vậy ảnh của G qua phép quay tâm O, góc quay 90° là G’.

Suy ra OG = OG’ và $\widehat{{\mathrm{GOG}}^{\text{'}}}=\left(\mathrm{OG},{\mathrm{OG}}^{\text{'}}\right)=90°$.

DOGG’ có OG = OG’ và $\widehat{{\mathrm{GOG}}^{\text{'}}}=90°$ nên là tam giác vuông cân tại O.

Vậy ∆OGG’ vuông cân tại O.