Toptailieu.vn biên soạn và giới thiệu lời giải Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 3: Phép đối xứng trục hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Chuyên đề Toán 11 Bài 3 từ đó học tốt môn Toán 11.

Chuyên đề Toán 11 (Chân trời sáng tạo) Bài 3: Phép đối xứng trục

Khởi động trang 14 Chuyên đề Toán 11: Trong các hình sau, hình nào có trục đối xứng?

Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?

Lời giải:

⦁ Trong các hình đã cho, cả ba hình đều có trục đối xứng là đường thẳng màu vàng ở mỗi hình.

⦁ Ta xét hình chiếc lá:

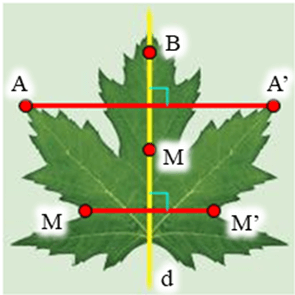
Lấy điểm A bất kì trên chiếc lá sao cho A không nằm trên trục đối xứng d của chiếc lá (hình vẽ).

Khi đó ta luôn xác định được một điểm A’ đối xứng với A qua d hay d là đường trung trực của đoạn thẳng AA’.

Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M không nằm trên d, ta đều xác định được một điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (1)

Lấy điểm B bất kì trên chiếc lá sao cho B nằm trên đường thẳng d (hình vẽ).

Khi đó ta có B đối xứng với chính nó qua d.

Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M nằm trên d thì ta luôn có M đối xứng với chính nó qua d (2)

Từ (1), (2), ta thu được phép biến hình biến một nửa chiếc lá thành nửa còn lại là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.

Chứng minh tương tự với hình cây thông và hình con bọ, ta cũng được kết quả như trên.

Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d của mỗi hình phẳng thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.

1. Định nghĩa

Khám phá 1 trang 15 Chuyên đề Toán 11: Cho đường thẳng d. Gọi f là quy tắc xác định như sau:

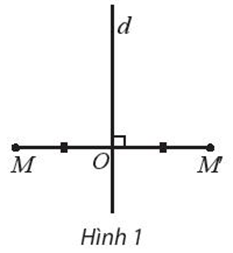
a) Với điểm M không thuộc d, xác định điểm M’ sao cho d là đường trung trực của MM’ (Hình 1).

b) Với điểm M thuộc d thì f biến điểm M thành chính nó.

Hỏi f có phải là phép biến hình hay không?

Lời giải:

Theo đề, ta có f(M) = M’.

Ta thấy f là quy tắc sao cho ứng với mỗi điểm M, ta đều xác định được duy nhất một điểm M’.

Vậy f là một phép biến hình.

2. Tính chất

Khám phá 2 trang 15 Chuyên đề Toán 11: Giả sử Đ_a là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy sao cho trục Ox trùng với a. Lấy hai điểm tùy ý A(x_A; y_A) và B(x_B; y_B). Gọi A’, B’ lần lượt là ảnh của A, B qua phép đối xứng trục a (Hình 3). Xác định tọa độ của A’ và B’ rồi dùng công thức tính khoảng cách để so sánh A’B’ và AB.

Lời giải:

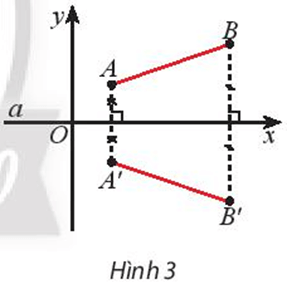
⦁ Ta có A’ là ảnh của A qua Đ_a.

Suy ra a là đường trung trực của đoạn thẳng AA’ hay Ox là đường trung trực của đoạn thẳng AA’.

Do đó A’ đối xứng với A qua Ox nên chúng có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ A’(x_A; –y_A).

Tương tự như vậy, ta được tọa độ B’(x_B; –y_B).

Vậy tọa độ A’(x_A; –y_A) và B’(x_B; –y_B).

⦁ Ta có $\overrightarrow{\mathrm{AB}}=\left(x_B-x_A;y_B-y_A\right)$.

Suy ra $\mathrm{AB}=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$.

Ta lại có $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}=\left(x_B-x_A;-y_B+y_A\right)$.

Suy ra:

$A^{\text{'}}{B}^{\text{'}}=\sqrt{{\left(x_B-x_A\right)}^2+{\left(-y_B+y_A\right)}^2}=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$.

Vậy A’B’ = AB.

Thực hành 1 trang 17 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – y + 3 = 0 và đường tròn (C): (x + 1)² + (y + 2)² = 9.

a) Tìm ảnh của đường thẳng d qua Đ_Oy.

b) Tìm ảnh của đường tròn (C) qua Đ_Ox.

Lời giải:

a) Trục Oy: x = 0.

Thế x = 0 vào phương trình d, ta được 0 – y + 3 = 0 ⇔ y = 3.

Suy ra giao điểm của d và Oy là P(0; 3).

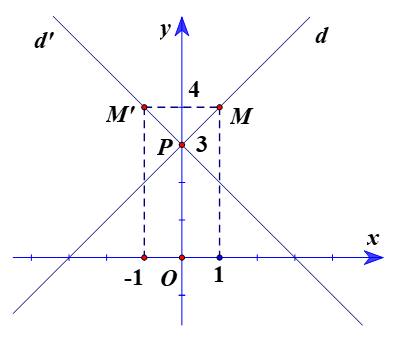
Chọn điểm M(1; 4) ∈ d: x – y + 3 = 0

Ta đặt M’ = Đ_Oy(M).

Suy ra Oy là đường trung trực của MM’ hay M’ là điểm đối xứng với M qua Oy.

Do đó hai điểm M và M’ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ điểm M’(–1; 4).

Ta có $\overrightarrow{M^{\text{'}}P}=\left(1;-1\right)$.

Gọi d’ là ảnh của d qua Đ_Oy.

Đường thẳng d’ có vectơ chỉ phương $\overrightarrow{M^{\text{'}}P}=\left(1;-1\right)$.

Suy ra d’ có vectơ pháp tuyến ${\overrightarrow{n}}_{d^{\text{'}}}=\left(1;1\right)$.

Vậy đường thẳng d’ đi qua P(0; 3) và có vectơ pháp tuyến ${\overrightarrow{n}}_{d^{\text{'}}}=\left(1;1\right)$ nên phương trình d’ là: 1.(x – 0) + 1.(y – 3) = 0 hay x + y – 3 = 0.

b) Đường tròn (C) có tâm I(–1; –2), bán kính R = 3.

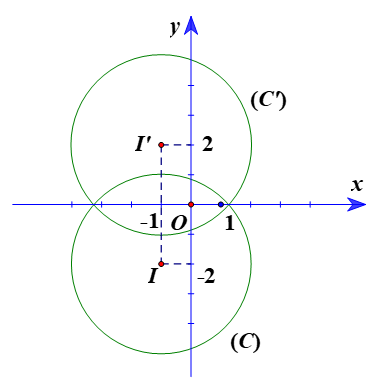
Ta đặt I’ = Đ_Ox(I).

Suy ra Ox là đường trung trực của II’ hay I’ đối xứng với I qua Ox

Do đó hai điểm I và I’ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ điểm I’(–1; 2).

Gọi (C’) là ảnh của đường tròn (C) qua Đ_Ox.

Suy ra (C’) có tâm I’(–1; 2), bán kính R’ = R = 3.

Vận dụng 1 trang 17 Chuyên đề Toán 11: Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d. Tìm trên bờ sông một địa điểm M để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất (Hình 7).

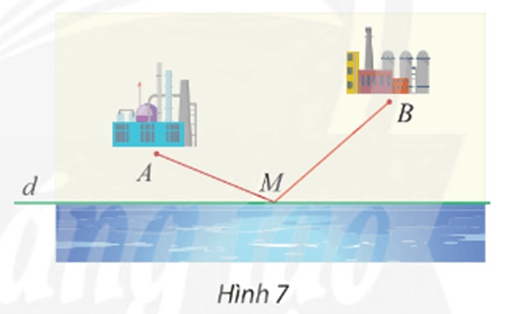
Lời giải:

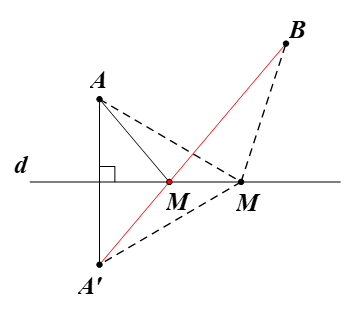
Gọi A’ là ảnh của A qua Đ_d.

Suy ra d là đường trung trực của đoạn thẳng AA’.

Mà M ∈ d (giả thiết), do đó MA = MA’.

Vì AB cố định nên A’B cũng cố định.

Ta có MA + MB = MA’ + MB ≥ A’B (theo bất đẳng thức tam giác).

Suy ra MA + MB ngắn nhất khi và chỉ khi MA + MB = A’B.

Tức là, ba điểm A’, M, B thẳng hàng hay M là giao điểm của A’B và d.

Vậy địa điểm M cần tìm là giao điểm của bờ sông (đường thẳng d) với đường thẳng A’B, trong đó A’ là ảnh của A qua Đ_d.

3. Trục đối xứng của một hình

Khám phá 3 trang 17 Chuyên đề Toán 11: Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.

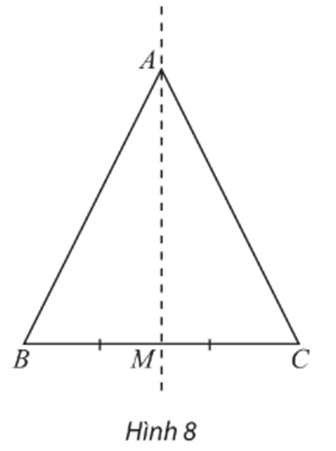
Lời giải:

Do A ∈ AM nên Đ_AM(A) = A.

Ta có tam giác ABC cân tại A có AM là đường trung tuyến.

Suy ra AM cũng là đường trung trực của tam giác ABC.

Do đó AM là đường trung trực của đoạn thẳng BC.

Vì vậy Đ_AM(B) = C và Đ_AM(C) = B.

Vậy ảnh của tam giác ABC qua phép đối xứng trục AM là tam giác ACB.

Thực hành 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.

Lời giải:

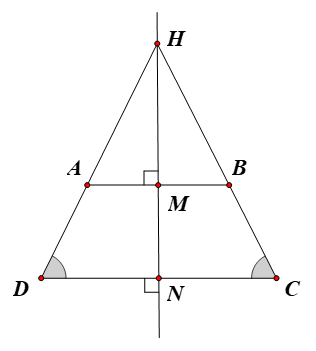
Gọi H là giao điểm của AD và BC.

Ta có $\widehat{\mathrm{ADC}}=\widehat{\mathrm{BCD}}$ (do ABCD là hình thang cân).

Suy ra tam giác HCD cân tại H.

Do đó HD = HC.

Vì vậy HD – AD = HC – BC (AD = BC vì ABCD là hình thang cân có hai đáy AB, CD).

Suy ra HA = HB.

Do đó tam giác HAB cân tại H.

Gọi M, N lần lượt là trung điểm của AB và CD.

Tam giác HCD cân tại H có HN là đường trung tuyến.

Suy ra HN cũng là đường cao của tam giác HCD, do đó HN ⊥ CD.

Chứng minh tương tự, ta được HM ⊥ AB.

Mà AB // CD (chứng minh trên).

Suy ra HM ⊥ CD

Lại có HN ⊥ CD (chứng minh trên).

Do đó ba điểm H, M, N thẳng hàng.

Ta có M là trung điểm AB và MN ⊥ AB (chứng minh trên).

Suy ra MN là đường trung trực của hai đoạn thẳng AB.

Khi đó B = Đ_MN(A) và A = Đ_MN(B).

Chứng minh tương tự, ta được D = Đ_MN(C) và C = Đ_MN(D).

Do đó ảnh của hình thang cân ABCD qua Đ_MN là chính nó.

Vậy trục đối xứng cần tìm là đường thẳng MN, với M, N lần lượt là trung điểm của AB và CD.

Vận dụng 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng trong các hình ở Hình 10.

Lời giải:

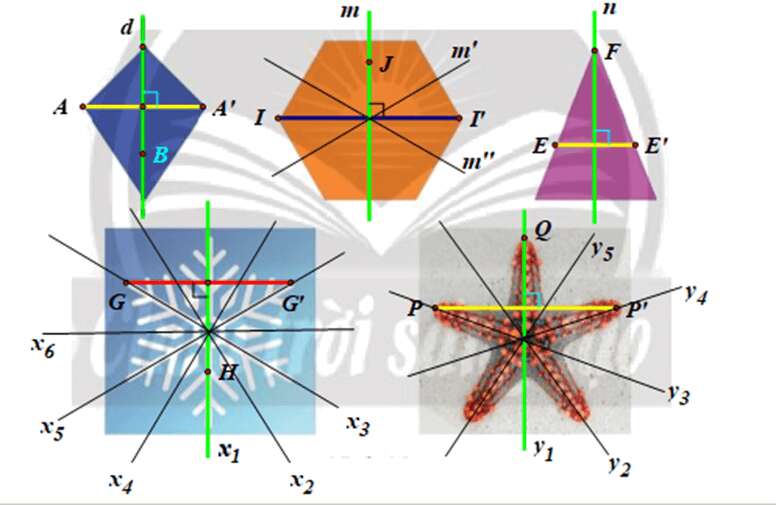
⦁ Ta xét hình tứ giác:

Chọn đường thẳng d như hình vẽ.

Lấy điểm A nằm trên hình tứ giác nhưng không nằm trên đường thẳng d.

Ta đặt A’ = Đ_d(A).

Khi đó A’ nằm trên hình tứ giác ban đầu.

Lấy điểm B nằm trên hình tứ giác và nằm trên đường thẳng d.

Ta thấy B = Đ_d(B).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tứ giác, ta cũng xác định được ảnh của các điểm đó qua Đ_d trên hình tứ giác ban đầu.

Do đó Đ_d biến hình tứ giác đã cho thành chính nó.

Vậy đường thẳng d như hình vẽ là trục đối xứng của hình tứ giác đã cho.

⦁ Ta xét hình lục giác:

Chọn đường thẳng m là đường trung trực của hai cạnh đối như hình vẽ.

Lấy điểm I nằm trên hình lục giác nhưng không nằm trên đường thẳng m.

Ta đặt I’ = Đ_m(I).

Khi đó I’ nằm trên hình lục giác ban đầu.

Lấy điểm J nằm trên hình lục giác và nằm trên đường thẳng m.

Ta thấy J = Đ_m(J).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình lục giác, ta cũng xác định được ảnh của các điểm đó qua Đ_m trên hình lục giác ban đầu.

Do đó Đ_m biến hình lục giác đã cho thành chính nó.

Vậy đường thẳng m như hình vẽ là trục đối xứng của hình lục giác đã cho.

Chú ý: Hình lục giác đều có 3 trục đối xứng (m, m’, m’’).

⦁ Ta xét hình tam giác cân:

Chọn đường thẳng n là đường trung trục của cạnh đáy như hình vẽ.

Lấy điểm E nằm trên hình tam giác nhưng không nằm trên đường thẳng n.

Ta đặt E’ = Đ_n(E).

Khi đó E’ nằm trên hình tam giác ban đầu.

Lấy điểm F nằm trên hình tam giác và nằm trên đường thẳng n.

Ta thấy F = Đ_n(F).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tam giác, ta cũng xác định được ảnh của các điểm đó qua Đ_n trên hình tam giác ban đầu.

Do đó Đ_n biến hình tam giác đã cho thành chính nó.

Vậy đường thẳng n là trục đối xứng của hình tam giác đã cho.

⦁ Ta xét hình bông tuyết:

Chọn đường thẳng x₁ như hình vẽ.

Lấy điểm G nằm trên hình bông tuyết nhưng không nằm trên đường thẳng x­₁.

Ta đặt $G^{\text{'}}={Đ}_{x_1}\left(G\right)$

Khi đó G’ nằm trên hình bông tuyết ban đầu.

Lấy điểm H nằm trên hình bông tuyết và nằm trên đường thẳng x₁.

Ta thấy $H={Đ}_{x_1}\left(H\right)$

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bông tuyết, ta cũng xác định được ảnh của các điểm đó qua ${\mathrm{Đ}}_{{\mathrm{x}}_1}$ trên hình bông tuyết ban đầu.

Do đó ${\mathrm{Đ}}_{{\mathrm{x}}_1}$ biến hình bông tuyết đã cho thành chính nó.

Vậy đường thẳng x₁ như hình vẽ là trục đối xứng của hình bông tuyết đã cho.

Chú ý: Hình bông tuyết này có 6 trục đối xứng (x₁, x₂, x₃, x₄, x₅, x₆).

⦁ Ta xét hình con sao biển:

Chọn đường thẳng y₁ như hình vẽ.

Lấy điểm P nằm trên hình con sao biển nhưng không nằm trên đường thẳng y₁.

Ta đặt $P^{\text{'}}={Đ}_{y_1}\left(P\right)$

Khi đó P’ nằm trên hình con sao biển ban đầu.

Lấy điểm Q nằm trên hình con sao biển và nằm trên đường thẳng y.

Ta thấy $Q={Đ}_{y_1}\left(Q\right)$

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình con sao biển, ta cũng xác định được ảnh của các điểm đó qua ${Đ}_{y_1}$trên hình con sao biển ban đầu.

Do đó ${Đ}_{y_1}$ biến hình con sao biển đã cho thành chính nó.

Vậy đường thẳng y₁ như hình vẽ là trục đối xứng của hình con sao biển đã cho.

Chú ý: Hình con sao biển có 5 trục đối xứng (y₁, y₂, y₃, y₄, y₅).

Bài tập

Bài 1 trang 18 Chuyên đề Toán 11: Vẽ các hình sau đây vào giấy kẻ ô vuông và tìm ảnh của các hình đã cho qua phép đối xứng trục d.

Lời giải:

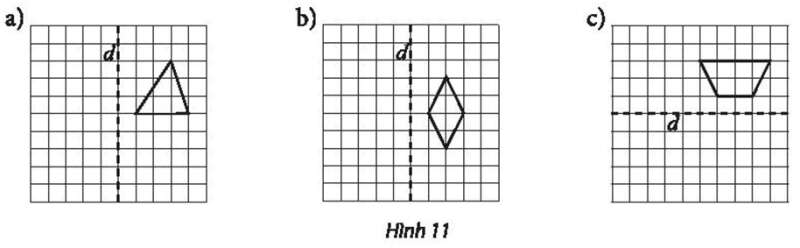
⦁ Hình 11a:

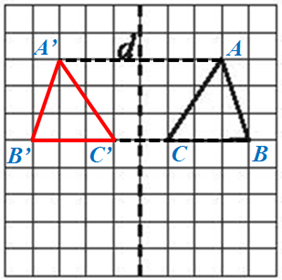
Ta đặt tam giác cần tìm ảnh qua phép đối xứng trục d là tam giác ABC (hình vẽ).

Vẽ A’, B’, C’ lần lượt đối xứng với A, B, C qua d.

Vậy ảnh của tam giác ABC ở Hình 11a qua phép đối xứng trục d là tam giác A’B’C’.

⦁ Hình 11b:

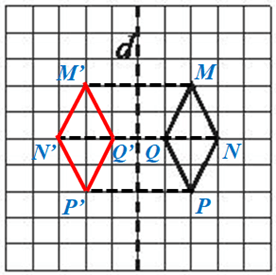
Ta đặt hình thoi cần tìm ảnh qua phép đối xứng trục d là hình thoi MNPQ (hình vẽ).

Vẽ M’, N’, P’, Q’ lần lượt đối xứng với M, N, P, Q qua d.

Vậy ảnh của hình thoi MNPQ ở Hình 11b qua phép đối xứng trục d là hình thoi M’N’P’Q’.

⦁ Hình 11c:

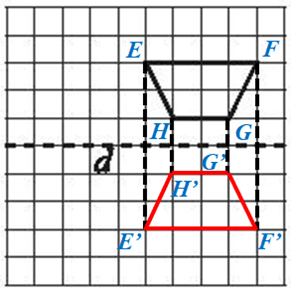
Ta đặt hình thang cần tìm ảnh qua phép đối xứng trục d là hình thang cân EFGH (hình vẽ).

Vẽ E’, F’, G’, H’ lần lượt đối xứng với E, F, G, H qua d.

Vậy ảnh của hình thang cân EFGH ở Hình 11c qua phép đối xứng trục d là hình thang cân E’F’G’H’.

Bài 2 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình x – y = 0 và cho điểm M(x₀; y₀). Tìm tọa độ điểm M’ = Đ_d(M).

Lời giải:

Trường hợp 1: M ∈ d.

Khi đó M = Đ_d(M).

Vì vậy M’ ≡ M.

Do đó M’(x₀; y₀).

Trường hợp 2: M ∉ d.

Theo đề, ta có M’ = Đ_d(M).

Suy ra d là đường trung trực của đoạn MM’, do đó d ⊥ MM’.

Đường thẳng d có vectơ pháp tuyến ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Vì vậy MM’ nhận ${\overrightarrow{n}}_d=\left(1;-1\right)$ làm vectơ chỉ phương.

Suy ra phương trình MM’: $\left\{\begin{array}{l}\mathrm{x}={\mathrm{x}}_0+\mathrm{t}\\ \mathrm{y}={\mathrm{y}}_0-\mathrm{t}\end{array}\right.$

Gọi H là giao điểm của MM’ và d.

Suy ra H là trung điểm MM’ và tọa độ H(x₀ + t; y₀ – t).

Ta có H ∈ d.

Suy ra x₀ + t – y₀ + t = 0.

⇔ $t=\frac{y_0-x_0}{2}$.

Do đó tọa độ $H\left(\frac{x_0+y_0}{2};\frac{x_0+y_0}{2}\right)$.

Ta có H là trung điểm MM’.

Suy ra $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{M}}^{\text{'}}}=2{\mathrm{x}}_{\mathrm{H}}-{\mathrm{x}}_{\mathrm{M}}=2.\frac{{\mathrm{x}}_0+{\mathrm{y}}_0}{2}-{\mathrm{x}}_0={\mathrm{y}}_0\\ {\mathrm{y}}_{{\mathrm{M}}^{\text{'}}}=2{\mathrm{y}}_{\mathrm{H}}-{\mathrm{y}}_{\mathrm{M}}=2.\frac{{\mathrm{x}}_0+{\mathrm{y}}_0}{2}-{\mathrm{y}}_0={\mathrm{x}}_0\end{array}\right.$

Do đó tọa độ M’(y₀; x₀).

Vậy $\left\{\begin{array}{l}{\mathrm{M}}^{\text{'}}\left({\mathrm{x}}_0;{\mathrm{y}}_0\right)\mathrm{khi}\mathrm{M}\in \mathrm{d}\\ {\mathrm{M}}^{\text{'}}\left({\mathrm{y}}_0;{\mathrm{x}}_0\right)\mathrm{khi}\mathrm{M}\notin \mathrm{d}\end{array}\right.$.

Bài 3 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).

a) Tìm ảnh của A qua Đ_Ox và ảnh của B qua Đ_Oy.

b) Biết M là ảnh của N qua Đ_Oy. Xác định tọa độ của N.

Lời giải:

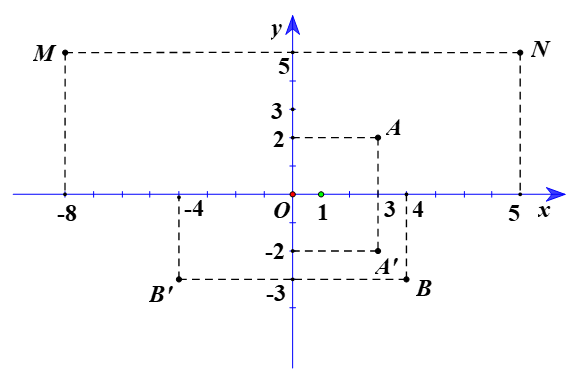
a) ⦁ Gọi A’ là ảnh của A qua Đ_Ox.

Suy ra Ox là đường trung trực của đoạn AA’ hay A’ đối xứng với A qua Ox

Do đó hai điểm A(3; 2) và A’ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ điểm A’(3; –2).

⦁ Gọi B’ là ảnh của B qua Đ_Oy.

Suy ra Oy là đường trung trực của đoạn BB’ hay B’ đối xứng với B qua Oy

Do đó hai điểm B(4; –3) và B’ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ điểm B’(–4; –3).

Vậy ảnh của A qua Đ_Ox là A’(3; –2) và ảnh của B qua Đ_Oy là B’(–4; –3).

b) Ta có M là ảnh của N qua Đ_Oy.

Suy ra Oy là đường trung trực của đoạn MN hay M và N đối xứng với nhau qua Oy

Do đó hai điểm M(–8; 5) và N có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ điểm N(8; 5).

Vậy tọa độ N(8; 5).

Bài 4 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)² + (y – 4)² = 25 và đường thẳng ∆: 2x + 3y + 4 = 0.

a) Tìm ảnh của (C) và ∆ qua phép đối xứng trục Ox.

b) Tìm ảnh của (C) và ∆ qua phép đối xứng trục Oy.

c) Tìm ảnh của (C) và ∆ qua phép đối xứng trục d: x – y – 3 = 0.

Lời giải:

Đường tròn (C) có tâm I(3; 4), bán kính R = 5.

a)

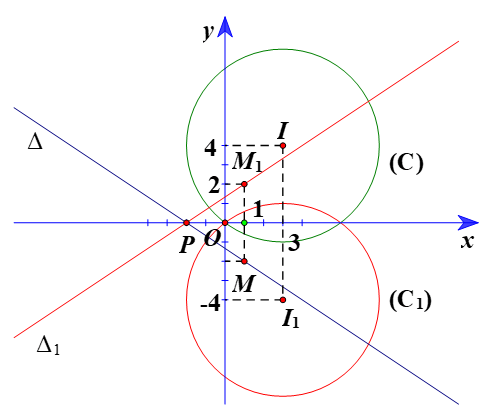
⦁ Gọi (C₁) là ảnh của (C) qua Đ_Ox, khi đó (C₁) có tâm I₁ là ảnh của I(3; 4) Đ_Ox và bán kính R₁ = R = 5.

Ta có I₁ = Đ_Ox(I).

Suy ra Ox là đường trung trực của đoạn II₁

Do đó hai điểm I(3; 4) và I₁ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ I₁(3; –4).

Vậy ảnh của đường tròn (C) qua Đ_Ox là đường tròn (C₁) có phương trình là:

(x – 3)² + (y + 4)² = 25.

⦁ Trục Ox: y = 0.

Với y = 0, ta có 2x + 3.0 + 4 = 0 ⇔ x = –2.

Suy ra giao điểm của ∆ và trục Ox là điểm P(–2; 0).

Khi đó P = Đ_Ox(P).

Chọn M(1; –2) ∈ ∆.

Gọi M₁ và ∆₁ theo thứ tự là ảnh của M và ∆ qua Đ_Ox.

Ta thấy Ox là đường trung trực của đoạn MM₁.

Do đó hai điểm M(1; –2) và M₁ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ M₁(1; 2).

Ta có $\overrightarrow{M_{1}P}=\left(-3;-2\right)$.

Đường thẳng ∆₁ có vectơ chỉ phương $\overrightarrow{M_{1}P}=\left(-3;-2\right)$.

Suy ra ∆₁ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_1}=\left(2;-3\right)$.

Vậy đường thẳng ∆₁ đi qua P(–2; 0) và có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_1}=\left(2;-3\right)$ nên có phương trình là:

2(x + 2) – 3(y – 0) = 0 hay 2x – 3y + 4 = 0.

b)

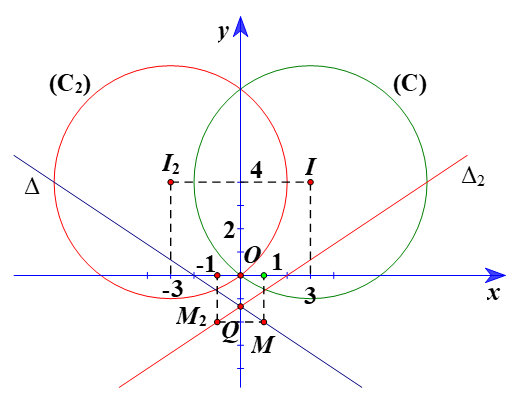
⦁ Gọi (C₂) là ảnh của (C) qua Đ_Oy, khi đó (C₂) có tâm I₂ là ảnh của I(3; 4) qua Đ_Oy và bán kính R₂ = R = 5.

Ta có I₂ = Đ_Oy(I).

Suy ra Oy là đường trung trực của đoạn II₂.

Do đó hai điểm I(3; 4) và I₂ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ I₂(–3; 4).

Vậy ảnh của đường tròn (C) qua Đ_Oy là đường tròn (C₂) có phương trình là:

(x + 3)² + (y – 4)² = 25.

⦁ Trục Oy: x = 0.

Với x = 0, ta có 2.0 + 3y + 4 = 0 ⇔ $y=-\frac{4}{3}$.

Suy ra giao điểm của ∆ và trục Oy là điểm $Q\left(0;-\frac{4}{3}\right)$.

Khi đó Q = Đ_Oy(Q).

Chọn M(1; –2) ∈ ∆.

Gọi M₂ và ∆₂ theo thứ tự là ảnh của M và ∆ qua Đ_Oy.

Ta thấy Oy là đường trung trực của đoạn MM₂.

Do đó hai điểm M(1; –2) và M₂ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ M₂(–1; –2).

Ta có $\overrightarrow{M_{2}Q}=\left(1;\frac{2}{3}\right)$.

Đường thẳng ∆₂ có vectơ chỉ phương ${\overrightarrow{u}}_2=3\overrightarrow{M_{2}Q}=\left(3;2\right)$.

Suy ra ∆₂ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_2}=\left(2;-3\right)$.

Vậy đường thẳng ∆₂ đi qua M₂(–1; –2) và có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_2}=\left(2;-3\right)$ nên có phương trình là:

2(x + 1) – 3(y + 2) = 0 hay 2x – 3y – 4 = 0.

c)

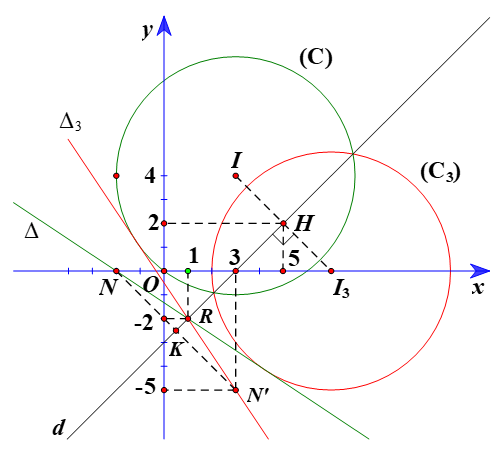
⦁ Gọi (C₃) là ảnh của (C) qua Đ_d, khi đó (C₂) có tâm I₃ là ảnh của I(3; 4) qua Đ_d và bán kính R₃ = R = 5.

Ta có I₃ = Đ_d(I).

Suy ra d là đường trung trực của đoạn II₃ nên II₃ ⊥ d tại trung điểm của II₃.

Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Suy ra đường thẳng II₃ có vectơ chỉ phương ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Do đó đường thẳng II₃ có vectơ pháp tuyến $\overrightarrow{u}=\left(1;1\right)$.

Vì vậy đường thẳng II₃ đi qua điểm I(3; 4) và nhận $\overrightarrow{u}=\left(1;1\right)$ làm vectơ pháp tuyến nên có phương trình là:

1(x – 3) + 1(y – 4) = 0 ⇔ x + y – 7 = 0.

Gọi H là giao điểm của II₃ và đường thẳng d.

Suy ra tọa độ H thỏa mãn hệ phương trình $\left\{\begin{array}{l}\mathrm{x}-\mathrm{y}-3=0\\ \mathrm{x}+\mathrm{y}-7=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=5\\ \mathrm{y}=2\end{array}\right.$

Do đó tọa độ H(5; 2).

Ta có H là trung điểm II₃.

Suy ra $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{I}}_3}=2{\mathrm{x}}_{\mathrm{H}}-{\mathrm{x}}_{\mathrm{I}}=2.5-3=7\\ {\mathrm{y}}_{{\mathrm{I}}_3}=2{\mathrm{y}}_{\mathrm{H}}-{\mathrm{y}}_{\mathrm{I}}=2.2-4=0\end{array}\right.$

Do đó tọa độ I₃(7; 0).

Vậy ảnh của đường tròn (C) qua Đ_d là đường tròn (C₃) có phương trình là:

(x – 7)² + y² = 25.

⦁ Gọi R là giao điểm của ∆ và d.

Suy ra tọa độ R thỏa mãn hệ phương trình:

$\left\{\begin{array}{l}2\mathrm{x}+3\mathrm{y}+4=0\\ \mathrm{x}-\mathrm{y}-3=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=1\\ \mathrm{y}=-2\end{array}\right.$

Do đó tọa độ R(1; –2).

Khi đó R = Đ_d(R).

Chọn N(–2; 0) ∈ ∆: 2x + 3y + 4 = 0.

Gọi N’ và ∆₃ theo thứ tự là ảnh của N và ∆ qua Đ_d.

Ta thấy d là đường trung trực của đoạn NN’.

Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Suy ra đường thẳng NN’ có vectơ chỉ phương ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Do đó đường thẳng NN’ có vectơ pháp tuyến $\overrightarrow{u}=\left(1;1\right)$.

Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận $\overrightarrow{u}=\left(1;1\right)$ làm vectơ pháp tuyến nên có phương trình là:

1(x + 2) + 1(y – 0) = 0 ⇔ x + y + 2 = 0.

Gọi K là giao điểm của NN’ và đường thẳng d.

Suy ra tọa độ K thỏa mãn hệ phương trình:

$\left\{\begin{array}{l}\mathrm{x}+\mathrm{y}+2=0\\ \mathrm{x}-\mathrm{y}-3=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=\frac{1}{2}\\ \mathrm{y}=-\frac{5}{2}\end{array}\right.$

Do đó tọa độ $K\left(\frac{1}{2};-\frac{5}{2}\right)$.

Ta có K là trung điểm NN’.

Suy ra $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{N}}^{\text{'}}}=2{\mathrm{x}}_{\mathrm{K}}-{\mathrm{x}}_{\mathrm{N}}=2.\frac{1}{2}+2=3\\ {\mathrm{y}}_{{\mathrm{N}}^{\text{'}}}=2{\mathrm{y}}_{\mathrm{K}}-{\mathrm{y}}_{\mathrm{N}}=2.\left(-\frac{5}{2}\right)-0=-5\end{array}\right.$

Do đó tọa độ N’(3; –5).

Với R(1; –2), ta có $\overrightarrow{N^{\text{'}}R}=\left(-2;3\right)$.

Đường thẳng ∆₃ có vectơ chỉ phương $\overrightarrow{N^{\text{'}}R}=\left(-2;3\right)$.

Suy ra ∆₃ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_3}=\left(3;2\right)$.

Vậy đường thẳng ∆₃ đi qua N’(3; –5) và nhận ${\overrightarrow{n}}_{{\Delta }_3}=\left(3;2\right)$ làm vectơ pháp tuyến nên có phương trình là:

3(x – 3) + 2(y + 5) = 0 hay 3x + 2y + 1 = 0.

Bài 5 trang 19 Chuyên đề Toán 11: Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C và đi qua A. Gọi D là giao điểm thứ hai của hai đường tròn nói trên (Hình 12). Khi A di động trên một đường tròn cố định (O) thì điểm D di động trên đường nào?

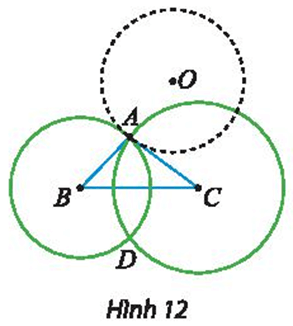
Lời giải:

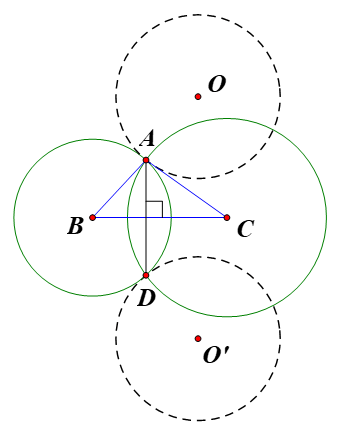
Gọi đường tròn (O’) là ảnh của đường tròn (O) qua Đ_BC.

Ta có đường tròn tâm B và đường tròn tâm C cắt nhau tại hai điểm A và D.

Suy ra BC là đường trung trực của đoạn AD.

Do đó D là ảnh của A qua Đ_BC.

Vậy khi điểm A di động trên đường tròn cố định (O) thì điểm D di động trên đường tròn cố định (O’), với (O’) là ảnh của (O) qua Đ_BC.

Bài 6 trang 19 Chuyên đề Toán 11: Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.

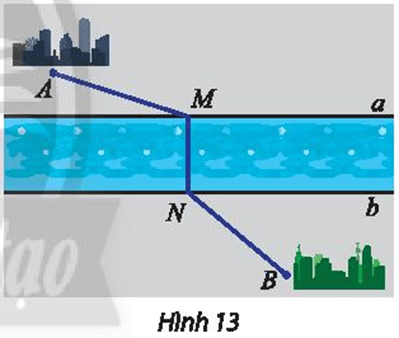
Lời giải:

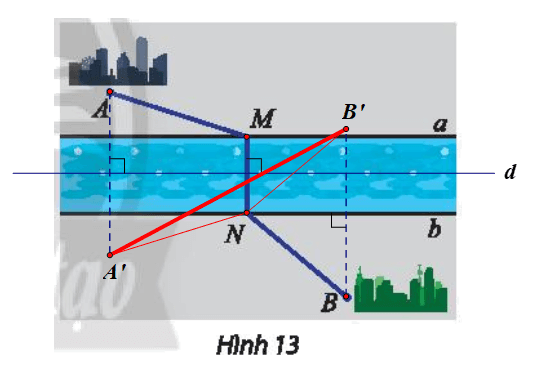
Gọi d là đường trung trực của đoạn MN.

Suy ra điểm N là ảnh của điểm M qua Đ_d.

Lấy điểm A’ là ảnh của điểm A qua Đ_d.

Suy ra đoạn A’N là ảnh của đoạn AM qua Đ_d.

Do đó A’N = AM.

Lấy điểm B’ là ảnh của điểm B qua Đ_b.

Suy ra b là đường trung trực của đoạn BB’.

Mà N ∈ b (giả thiết).

Do đó NB’ = NB.

Ta có AM + NB = A’N + NB’.

Áp dụng bất đẳng thức tam giác cho ∆A’NB’, ta được: A’N + NB’ ≥ A’B’.

Do đó tổng khoảng cách AM + NB ngắn nhất khi và chỉ khi A’N + NB’ = A’B’.

Tức là, ba điểm A’, N, B’ thẳng hàng.

Vậy N là giao điểm của A’B’ và bờ b, M là điểm nằm bên bờ a thỏa mãn M = Đ_d(N), với d là đường trung trực của đoạn MN, A’ = Đ_d(A), B’ = Đ_b(B).

Bài 7 trang 19 Chuyên đề Toán 11: Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.

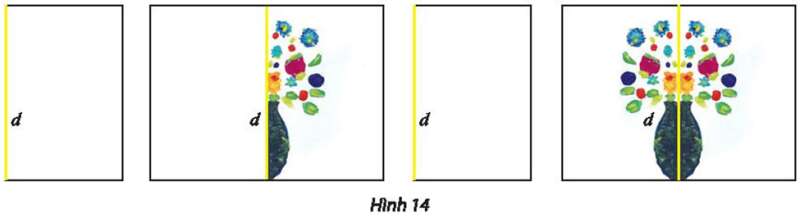
– Gấp đôi một tờ giấy trắng A4 theo nếp gấp d.

– Mở tờ giấy ra, ở một phía của nếp gấp d, nhỏ vài giọt màu nước có màu khác nhau làm hoa và một giọt màu đen làm bình hoa.

– Gấp lại tờ giấy theo nếp gấp d, chà nhẹ để màu thấm đều sang hai bên.

– Mở tờ giấy ra, ta có một bình hoa đẹp.

Tìm trục đối xứng của hình vừa vẽ.

Lời giải:

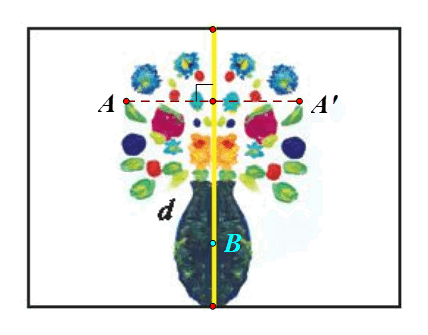
Lấy điểm A nằm trên hình bình hoa vừa vẽ nhưng không nằm trên đường thẳng d.

Ta đặt A’ = Đ_d(A).

Khi đó A’ nằm trên hình bình hoa vừa vẽ.

Lấy điểm B nằm trên hình bình hoa vừa vẽ và nằm trên đường thẳng d.

Ta thấy B = Đ_d(B).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bình hoa vừa vẽ, ta đều xác định được ảnh của các điểm đó qua Đ_d trên hình bình hoa vừa vẽ.

Do đó Đ_d biến hình bình hoa vừa vẽ thành chính nó.

Vậy đường thẳng d là trục đối xứng của hình bình hoa vừa vẽ.