Với giải Bài 3 trang 19 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài 3: Phép đối xứng trục giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5). Tìm ảnh của A
Bài 3 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
a) Tìm ảnh của A qua ĐOx và ảnh của B qua ĐOy.
b) Biết M là ảnh của N qua ĐOy. Xác định tọa độ của N.
Lời giải:
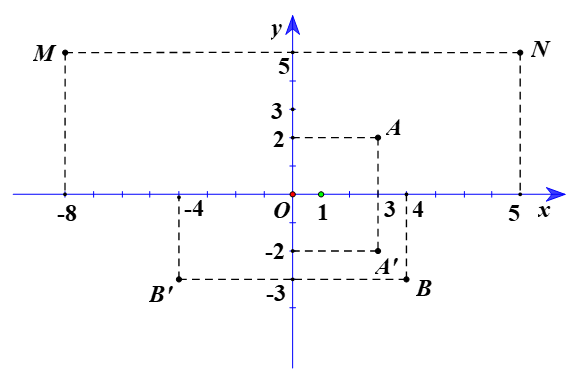
a) ⦁ Gọi A’ là ảnh của A qua ĐOx.
Suy ra Ox là đường trung trực của đoạn AA’ hay A’ đối xứng với A qua Ox
Do đó hai điểm A(3; 2) và A’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm A’(3; –2).
⦁ Gọi B’ là ảnh của B qua ĐOy.
Suy ra Oy là đường trung trực của đoạn BB’ hay B’ đối xứng với B qua Oy
Do đó hai điểm B(4; –3) và B’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm B’(–4; –3).
Vậy ảnh của A qua ĐOx là A’(3; –2) và ảnh của B qua ĐOy là B’(–4; –3).
b) Ta có M là ảnh của N qua ĐOy.
Suy ra Oy là đường trung trực của đoạn MN hay M và N đối xứng với nhau qua Oy
Do đó hai điểm M(–8; 5) và N có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm N(8; 5).
Vậy tọa độ N(8; 5).
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 14 Chuyên đề Toán 11: Trong các hình sau, hình nào có trục đối xứng?
Khám phá 1 trang 15 Chuyên đề Toán 11: Cho đường thẳng d. Gọi f là quy tắc xác định như sau:
Khám phá 2 trang 15 Chuyên đề Toán 11: Giả sử Đa là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy sao cho trục Ox trùng với a. Lấy hai điểm tùy ý A(xA; yA) và B(xB; yB). Gọi A’, B’ lần lượt là ảnh của A, B qua phép đối xứng trục a (Hình 3). Xác định tọa độ của A’ và B’ rồi dùng công thức tính khoảng cách để so sánh A’B’ và AB.
Thực hành 1 trang 17 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – y + 3 = 0 và đường tròn (C): (x + 1)2 + (y + 2)2 = 9.
Vận dụng 1 trang 17 Chuyên đề Toán 11: Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d. Tìm trên bờ sông một địa điểm M để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất (Hình 7).
Khám phá 3 trang 17 Chuyên đề Toán 11: Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.
Thực hành 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.
Vận dụng 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng trong các hình ở Hình 10.
Bài 1 trang 18 Chuyên đề Toán 11: Vẽ các hình sau đây vào giấy kẻ ô vuông và tìm ảnh của các hình đã cho qua phép đối xứng trục d.
Bài 2 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình x – y = 0 và cho điểm M(x0; y0). Tìm tọa độ điểm M’ = Đd(M).
Bài 3 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
Bài 4 trang 19 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 25 và đường thẳng ∆: 2x + 3y + 4 = 0.
Bài 5 trang 19 Chuyên đề Toán 11: Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C và đi qua A. Gọi D là giao điểm thứ hai của hai đường tròn nói trên (Hình 12). Khi A di động trên một đường tròn cố định (O) thì điểm D di động trên đường nào?
Bài 6 trang 19 Chuyên đề Toán 11: Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.
Bài 7 trang 19 Chuyên đề Toán 11: Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.
