Với giải Vận dụng 2 trang 18 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài 3: Phép đối xứng trục giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Tìm trục đối xứng trong các hình ở Hình 10

Vận dụng 2 trang 18 Chuyên đề Toán 11: Tìm trục đối xứng trong các hình ở Hình 10.

Lời giải:

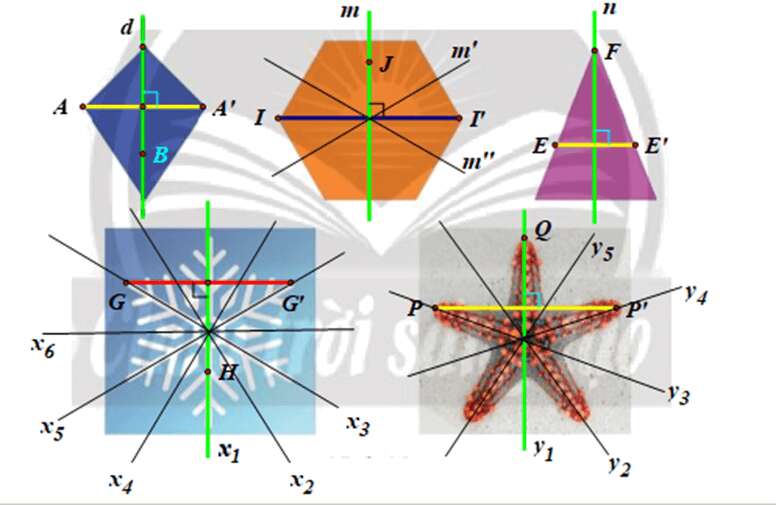
⦁ Ta xét hình tứ giác:

Chọn đường thẳng d như hình vẽ.

Lấy điểm A nằm trên hình tứ giác nhưng không nằm trên đường thẳng d.

Ta đặt A’ = Đ_d(A).

Khi đó A’ nằm trên hình tứ giác ban đầu.

Lấy điểm B nằm trên hình tứ giác và nằm trên đường thẳng d.

Ta thấy B = Đ_d(B).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tứ giác, ta cũng xác định được ảnh của các điểm đó qua Đ_d trên hình tứ giác ban đầu.

Do đó Đ_d biến hình tứ giác đã cho thành chính nó.

Vậy đường thẳng d như hình vẽ là trục đối xứng của hình tứ giác đã cho.

⦁ Ta xét hình lục giác:

Chọn đường thẳng m là đường trung trực của hai cạnh đối như hình vẽ.

Lấy điểm I nằm trên hình lục giác nhưng không nằm trên đường thẳng m.

Ta đặt I’ = Đ_m(I).

Khi đó I’ nằm trên hình lục giác ban đầu.

Lấy điểm J nằm trên hình lục giác và nằm trên đường thẳng m.

Ta thấy J = Đ_m(J).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình lục giác, ta cũng xác định được ảnh của các điểm đó qua Đ_m trên hình lục giác ban đầu.

Do đó Đ_m biến hình lục giác đã cho thành chính nó.

Vậy đường thẳng m như hình vẽ là trục đối xứng của hình lục giác đã cho.

Chú ý: Hình lục giác đều có 3 trục đối xứng (m, m’, m’’).

⦁ Ta xét hình tam giác cân:

Chọn đường thẳng n là đường trung trục của cạnh đáy như hình vẽ.

Lấy điểm E nằm trên hình tam giác nhưng không nằm trên đường thẳng n.

Ta đặt E’ = Đ_n(E).

Khi đó E’ nằm trên hình tam giác ban đầu.

Lấy điểm F nằm trên hình tam giác và nằm trên đường thẳng n.

Ta thấy F = Đ_n(F).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tam giác, ta cũng xác định được ảnh của các điểm đó qua Đ_n trên hình tam giác ban đầu.

Do đó Đ_n biến hình tam giác đã cho thành chính nó.

Vậy đường thẳng n là trục đối xứng của hình tam giác đã cho.

⦁ Ta xét hình bông tuyết:

Chọn đường thẳng x₁ như hình vẽ.

Lấy điểm G nằm trên hình bông tuyết nhưng không nằm trên đường thẳng x­₁.

Ta đặt $G^{\text{'}}={Đ}_{x_1}\left(G\right)$

Khi đó G’ nằm trên hình bông tuyết ban đầu.

Lấy điểm H nằm trên hình bông tuyết và nằm trên đường thẳng x₁.

Ta thấy $H={Đ}_{x_1}\left(H\right)$

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bông tuyết, ta cũng xác định được ảnh của các điểm đó qua ${\mathrm{Đ}}_{{\mathrm{x}}_1}$ trên hình bông tuyết ban đầu.

Do đó ${\mathrm{Đ}}_{{\mathrm{x}}_1}$ biến hình bông tuyết đã cho thành chính nó.

Vậy đường thẳng x₁ như hình vẽ là trục đối xứng của hình bông tuyết đã cho.

Chú ý: Hình bông tuyết này có 6 trục đối xứng (x₁, x₂, x₃, x₄, x₅, x₆).

⦁ Ta xét hình con sao biển:

Chọn đường thẳng y₁ như hình vẽ.

Lấy điểm P nằm trên hình con sao biển nhưng không nằm trên đường thẳng y₁.

Ta đặt $P^{\text{'}}={Đ}_{y_1}\left(P\right)$

Khi đó P’ nằm trên hình con sao biển ban đầu.

Lấy điểm Q nằm trên hình con sao biển và nằm trên đường thẳng y.

Ta thấy $Q={Đ}_{y_1}\left(Q\right)$

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình con sao biển, ta cũng xác định được ảnh của các điểm đó qua ${Đ}_{y_1}$trên hình con sao biển ban đầu.

Do đó ${Đ}_{y_1}$ biến hình con sao biển đã cho thành chính nó.

Vậy đường thẳng y₁ như hình vẽ là trục đối xứng của hình con sao biển đã cho.

Chú ý: Hình con sao biển có 5 trục đối xứng (y₁, y₂, y₃, y₄, y₅).