Toptailieu.vn xin giới thiệu Lý thuyết Tứ giác (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 8. Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Tứ giác (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 8
Bài giải Bài 10: Tứ giác
A. Lý thuyết Tứ giác
1. Khái niệm
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ:
Đặc điểm
+ Có 4 đỉnh
+ Có 4 cạnh
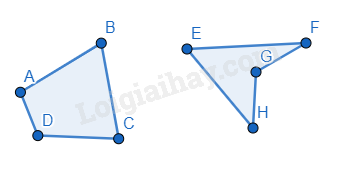
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất
+ Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng 360o.
Tứ giác ABCD, 
+ 
+ 
+ 
= 360o
Ví dụ:
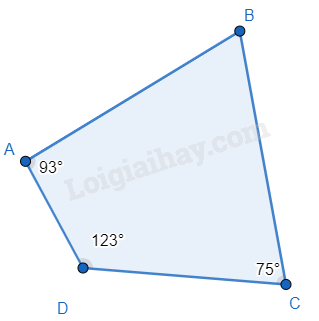
= 360o - 93o - 123o - 75o = 69o
B. Bài tập Tứ giác
Đang cập nhật ...
Xem thêm các bài lý thuyết Toán 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
