Toptailieu.vn biên soạn và giới thiệu lời giải Toán 8 (Kết nối tri thức) Bài 10: Tứ giác hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 8 Bài 10 từ đó học tốt môn Toán lớp 8.

Toán 8 (Kết nối tri thức) Bài 10: Tứ giác

Mở đầu trang 48 Toán 8 Tập 1: Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.

- Em có thể ghép bốn tứ giác khít nhau như vậy không?

- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

Lời giải:

- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.

Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.

- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.

Khi đó: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ (phần này sẽ được tìm hiểu ở mục 2, trang 50 SGK Toán 8 – Tập 1).

1. Tứ giác lồi

Câu hỏi trang 49 Toán 8 Tập 1: Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.

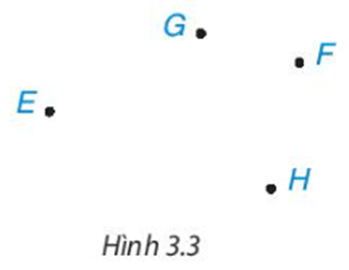
Lời giải:

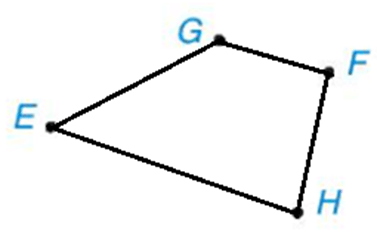
Nối EG, GF, FH, HE, ta được tứ giác EGFH như hình vẽ.

Luyện tập 1 trang 49 Toán 8 Tập 1: Quan sát tứ giác ABCD trong Hình 3.4.

- Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.

- Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.

- Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

Lời giải:

– Đường chéo còn lại của tứ giác ABCD là BD.

– Cặp cạnh đối còn lại của tứ giác ABCD là cặp cạnh AD và BC.

– Cặp góc đối còn lại của tứ giác ABCD là cặp góc B và D.

2. Tổng các góc của một tứ giác

HĐ trang 50 Toán 8 Tập 1: Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ của tứ giác ABCD.

Lời giải:

Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:

$\hat{A}+{\hat{B}}_1+{\hat{D}}_1=180°$;

$\hat{C}+{\hat{B}}_2+{\hat{D}}_2=180°$.

Khi đó, tứ giác ABCD có:

$\hat{A}+\hat{B}+\hat{C}+\hat{D}=\hat{A}+{\hat{B}}_1+{\hat{D}}_1+\hat{C}+{\hat{B}}_2+{\hat{D}}_2=180°+180°=360°$.

Vậy $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ .

Luyện tập 2 trang 50 Toán 8 Tập 1: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.

Lời giải:

Xét tứ giác EFGH có:

$\hat{E}+\hat{F}+\hat{G}+\hat{H}=360°$ (định lí tổng các góc trong một tứ giác).

Hay $90°+\hat{F}+90°+55°=360°$

Suy ra $\hat{F}+235°=360°$

Do đó $\hat{F}=360°-235°=125°$ .

Vậy $\hat{F}=125°$.

Vận dụng trang 50 Toán 8 Tập 1: Giải bài toán mở đầu.

Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.

- Em có thể ghép bốn tứ giác khít nhau như vậy không?

- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

Lời giải:

- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.

Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.

- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.

Khi đó: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ .

Thử thách nhỏ trang 50 Toán 8 Tập 1: Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?

Lời giải:

• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90^o).

Khi đó, tổng 4 góc nhỏ hơn: 4.90^o = 360^o (vô lí vì tổng 4 góc trong tứ giác bằng 360^o).

• Nếu tứ giác có 3 góc nhọn(nhỏ hơn 90^o); 1 góc tù (góc lớn hơn 90^o).

Khi đó, tổng 3 góc nhọn nhỏ hơn: 3.90^o = 270^o;

Số đo góc còn lại lớn hơn: 360^o – 270^o = 90^o (thỏa mãn).

Do đó,một tứ giác có thể có nhiều nhất 3 góc nhọn.

• Nếu 4 góc tứ giác đều tù(mỗi góc lớn hơn 90^o).

Khi đó, tổng 4 góc lớn hơn: 4.90^o = 360^o (vô lí vì tổng 4 góc trong một tứ giác bằng 360^o).

• Nếu tứ giác có 3 góc tù và 1 góc nhọn.

Tổng 3 góc tù lớn hơn: 3.90^o = 270^o;

Số đo góc còn lại của tứ giác nhỏ hơn: 360^o – 270^o = 90^o (thỏa mãn).

Do đó,một tứ giác có thể có nhiều nhất 3 góc tù.

Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.

Bài tập

Bài 3.1 trang 51 Toán 8 Tập 1: Tính góc chưa biết của các tứ giác trong Hình 3.8.

Trả lời:

• Hình 3.8a)

Xét tứ giác ABCD có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ .

Hay $90°+90°+\hat{C}+90°=360°$ .

Khi đó $\hat{C}+270°=360°$ .

Do đó $\hat{C}=360°-270°=90°$ .

Vậy $\hat{C}=90°$ .

• Hình 3.8b)

Vì $\widehat{VUS}$ và $\widehat{VUx}$ là hai góc kề bù nên ta có: $\widehat{VUS}+\widehat{VUx}=180°$

Hay $\widehat{VUS}+60°=180°$ .

Suy ra $\widehat{VUS}=180°-60°=120°$ .

Vì $\widehat{USR}$ và $\widehat{USy}$ là hai góc kề bù nên ta có: $\widehat{USR}+\widehat{USy}=180°$

Hay $\widehat{USR}+110°=180°$ .

Suy ra $\widehat{USR}=180°-110°=70°$ .

Do đó $\widehat{USR}=70°$ .

Xét tứ giác VUSR có: $\hat{V}+\widehat{VUS}+\widehat{USR}+\hat{R}=360°$ .

Hay $90°+120°+70°+\hat{R}=360°$

Khi đó $280°+\hat{R}=360°$

Do đó $\hat{R}=360°-280°=80°$ .

Vậy $\hat{R}=80°$ .

Bài 3.2 trang 51 Toán 8 Tập 1: Tính góc chưa biết của tứ giác trong Hình 3.9. Biết rằng $\hat{H}=\hat{E}+10°$ .

Lời giải:

Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:

$\hat{H}+\hat{E}+\hat{F}+\hat{G}=360°$

$\hat{E}+10°+\hat{E}+50°+60°=360°$

$2\hat{E}+120°=360°$

Suy ra $2\hat{E}=360°-120°=240°$ .

Khi đó $\hat{E}=120°$ .

Suy ra $\hat{H}=\hat{E}+10°=120°+10°=130°$ .

Vậy $\hat{H}=130°$ ; $\hat{E}=120°$ .

Bài 3.3 trang 51 Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.

b) Tính các góc B, D biết rằng $\hat{A}=100°,\hat{C}=60°$ .

Lời giải:

a) Nối AC, BD (như hình vẽ).

Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;

CB = CD hay hai điểm C cách đều hai đầu mút B và D;