Toptailieu biên soạn và giới thiệu lời Giải Toán 8 Bài tập cuối chương 2 trang 47 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 8 Bài tập cuối chương 2 trang 47 từ đó học tốt môn Toán 8.
Nội dung bài viết
Toán 8 (Kết nối tri thức) Bài tập cuối chương 2 trang 47
A. Trắc nghiệm
Chọn phương án đúng trong những câu sau:
Bài 2.28 trang 47 Toán 8 Tập 1: Đa thức x2−9x+8 được phân tích thành tích của hai đa thức
Lời giải:
x2−9x+8=x2−x−8x+8=(x2−x)−(8x−8)=x(x−1)−8(x−1)=(x−1)(x−8)
Chọn B.
Bài 2.29 trang 47 Toán 8 Tập 1: Khẳng định nào sau đây là đúng?
Lời giải:
A2−B2=(A−B)(A+B)
Chọn D.
Bài 2.30 trang 47 Toán 8 Tập 1: Biểu thức 25x2+20xy+4y2 viết dưới dạng bình phương của một tổng là:
Lời giải:
25x2+20xy+4y2=(5x)2+2.5x.2y+(2y)2=(5x+2y)2
Chọn D.
Bài 2.31 trang 47 Toán 8 Tập 1: Rút gọn biểu thức A=(2x+1)3−6x(2x+1) ta được
Lời giải:
A=(2x+1)3−6x(2x+1)=(2x)3+3.(2x)2.1+3.2x.12+13−(6x.2x+6x.1)=8x3+12x2+6x+1−12x2−6x=8x3+(12x2−12x2)+(6x−6x)+1=8x3+1
Chọn C.
B. Tự luận
Bài 2.32 trang 47 Toán 8 Tập 1: Tính nhanh giá trị của các biểu thức:
Lời giải:
a) x2−4x+4=x2−2.x.2+22=(x−2)2
Thay x=102 vào biểu thức ta được (102−2)2=1002=10000
b) x3+3x2+3x+1=(x+1)3
Thay x=999 vào biểu thức ta được (999+1)3=10003=1000000000
Bài 2.33 trang 47 Toán 8 Tập 1: Rút gọn các biểu thức:
a) (2x−5y)(2x+5y)+(2x+5y)2
b) (x+2y)(x2−2xy+4y2)+(2x−y)(4x2+2xy+y2)
Lời giải:
a)
(2x−5y)(2x+5y)+(2x+5y)2=(2x+5y)(2x−5y+2x+5y)=(2x+5y).4x=2x.4x+5y.4x=8x2+20xy
b)
(x+2y)(x2−2xy+4y2)+(2x−y)(4x2+2xy+y2)=x3+(2y)3+(2x)3−y3=x3+8y3+8x3−y3=(x3+8x3)+(8y3−y3)=9x3+7y3
Bài 2.34 trang 47 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
Lời giải:
a)
6x2−24y2=6.(x2−4y2)=6[x2−(2y)2]=6(x−2y)(x+2y)
b)
64x3−27y3=(4x)3−(3y)3=(4x-3y)[(4x)2+4x.3y+(3y)2]=(4x-3y)(16x2+12xy+9y2)
c) x4−2x3+x2=x2.(x2−2x+1)=x2.(x−1)2
d)
(x−y)3+8y3=(x−y)3+(2y)3=(x−y+2y)[(x−y)2−(x−y).2y+(2y)2]=(x+y)(x2−2xy+y2−2xy+2y2+4y2)=(x+y)(x2+7y2)
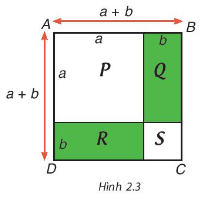
Lời giải:
Diện tích hình vuông ABCD là: (a+b)2
Diện tích hình vuông ABCD là:
SABCD=SP+SQ+SR+SS
=a2+ab+ab+b2=a2+2ab+b2
Do đó (a+b)2=a2+2ab+b2
Xem thêm các bài giải Toán 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.