Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 8 Bài tập cuối chương 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 8 Bài tập cuối chương 2.

SBT Toán 8 (Kết nối tri thức) Bài tập cuối chương 2

Trang 29 sách bài tập Toán 8 Tập 1

Câu 1 trang 29 sách bài tập Toán 8 Tập 1: Trong các đẳng thức sau, cái nào là hằng đẳng thức?

A. a(a + 1) = a + 1.

B. a² – 1 = a.

C. (a + b)(a – b) = a² + b².

D. (a + 1)(a + 2) = a² + 3a + 2.

Lời giải:

Đáp án đúng là: D

Ta có: (a + 1)(a + 2) = a² + 2a + a + 2 = a² + 3a + 2.

Do đó đẳng thức trên là một hằng đẳng thức.

Các đẳng thức còn lại, khi thay một giá trị a, b bất kì vào hai vế ta được kết quả không bằng nhau nên không phải là hằng đẳng thức.

Câu 2 trang 29 sách bài tập Toán 8 Tập 1: Đa thức x³ – 8 được phân tích thành tích của hai đa thức

A. x − 2 và x² − 2x – 4.

B. x − 2 và x² + 2x – 4.

C. x − 2 và x² + 2x + 4.

D. x − 2 và x² – 2x + 4.

Lời giải:

Đáp án đúng là: C

Ta có: x³ – 8 = x³ ‒ 2³ = (x ‒ 2)(x² + 2x + 4).

Câu 3 trang 29 sách bài tập Toán 8 Tập 1: Biểu thức $x^2+x+\frac{1}{4}$ viết được dưới dạng bình phương của một tổng là

A. ${\left(x+\left(-\frac{1}{2}\right)\right)}^2$.

B. ${\left(x+\frac{1}{2}\right)}^2$.

C. ${\left(2x+\frac{1}{2}\right)}^2$.

D. ${\left(\frac{1}{2}x+1\right)}^2$.

Lời giải:

Đáp án đúng là: B

Ta có: $x^2+x+\frac{1}{4}=x^2+2.x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2={\left(x+\frac{1}{2}\right)}^2$.

Câu 4 trang 29 sách bài tập Toán 8 Tập 1: Khẳng định nào sau đây là đúng?

A. (A – B)(A² – AB + B²) = A³ – B³.

B. (A + B)(A² + AB + B²) = A³ + B³.

C. (A + B)(A² – AB + B²) = A³ – B³.

D. (A + B)(A² – AB + B²) = A³ + B³.

Lời giải:

Đáp án đúng là: D

Ta có:

•A³ + B³ = (A + B)(A² – AB + B²);

• A³ – B³ = (A – B)(A² + AB + B²).

Do đó phương án D là đúng.

Câu 5 trang 29 sách bài tập Toán 8 Tập 1: Rút gọn biểu thức (x + 1)(x − 1) − (x + 2)(x − 2) ta được

A. 5.

B. 4.

C. 3.

D. –3.

Lời giải:

Đáp án đúng là: C

Ta có: (x + 1)(x − 1) − (x + 2)(x − 2)

= x² ‒ 1 ‒ (x² ‒ 2²)

= x² ‒ 1 ‒ x² + 4 = 3.

Bài 2.19 trang 29 sách bài tập Toán 8 Tập 1: Tính nhanh giá trị của các biểu thức:

a) x² + 12x + 36 tại x = −1006;

b) x³ – 9x² + 27x – 27 tại x = 103.

Lời giải:

a) x² + 12x + 36 = x² + 2.x.6 + 6² = (x + 6)²

Tại x = −1006 ta có:

(‒1006 + 6)² = 1000² = 1 000 000.

b) x³ – 9x² + 27x – 27 = x³ ‒ 3.x².3 + 3.x.3² ‒ 3³ = (x ‒ 3)³

Tại x = 103 ta có:

(103 ‒ 3)³ = 100³ = 1 000 000.

Trang 30 sách bài tập Toán 8 Tập 1

Bài 2.20 trang 30 sách bài tập Toán 8 Tập 1: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

a) (x + 1)³ – (x – 1)³ – 6x²;

b) (2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3);

c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4).

Lời giải:

a) Cách 1:

(x + 1)³ – (x – 1)³ – 6x²

= x³ + 3x² + 3x + 1 ‒ (x³ ‒ 3x² + 3x ‒ 1) ‒ 6x²

= x³ + 3x² + 3x + 1 ‒ x³ + 3x² ‒ 3x + 1 ‒ 6x²

= (x³ ‒ x³) + (3x² + 3x² ‒ 6x²) + (3x ‒ 3x) + 1 + 1

= 2.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Cách 2:

(x + 1)³ – (x – 1)³ – 6x²

= (x + 1 – x + 1)[(x + 1)² + (x + 1)(x – 1) + (x – 1)²] – 6x²

= 2(x² + 2x + 1 + x² – 1 + x² – 2x + 1) – 6x²

= 2(3x² + 1) – 6x²

= 6x² + 2 – 6x²

= 2.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

b) Cách 1:

(2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

= 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 2(4x² ‒ 9)

= 4x² ‒ 12x + 9 + 4x² + 12x + 9 ‒ 8x² + 18

= (4x² + 4x² ‒ 8x²) + (‒12x + 12x) + 9 + 18 = 36.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Cách 2:

(2x – 3)² + (2x + 3)² – 2(2x – 3)(2x + 3)

= (2x – 3)² – 2.(2x – 3).(2x + 3) + (2x + 3)²

= [2x – 3 – (2x + 3)]²

= (2x – 3 – 2x – 3)²

= (–6)² = 36.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

c) (x – 3)(x² + 3x + 9) – (x + 2)(x² – 2x + 4)

= (x – 3)(x² + 3x + 3²) – (x + 2)(x² – 2x + 2²)

= x³ ‒ 3³ ‒ (x³ + 2³)

= x³ ‒ 27 ‒ x³ ‒ 8

= (x³ ‒ x³) ‒ 27 ‒ 8 = ‒35.

Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến x.

Bài 2.21 trang 30 sách bài tập Toán 8 Tập 1: Không cần tính, hãy so sánh số A với số B trong các trường hợp sau:

a) A = 2021 . 2023 và B = 2022²;

b) A = 2021 . 2025 và B = 2023².

Lời giải:

a) Ta có A = 2021 . 2023

= (2022 – 1).(2022 + 1)

= 2022² – 1 < 2022².

Vậy A < B.

b) A = 2021 . 2025

= (2023 – 2)(2023 + 2)

= 2023² – 2 < 2023².

Vậy A < B.

Bài 2.22 trang 30 sách bài tập Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x³ – y³ + 2x – 2y;

b) x² + 8xy + 16y² – 4z².

Lời giải:

a) x³ – y³ + 2x – 2y

= (x³ – y³) + (2x – 2y)

= (x − y)(x² + xy + y²) + 2(x – y)

= (x − y)(x² + xy + y² + 2);

b) x² + 8xy + 16y² – 4z²

= (x² + 8xy + 16y²) – 4z²

= (x + 4y)² – (2z)²

= (x + 4y – 2z)(x + 4y + 2z).

Bài 2.23 trang 30 sách bài tập Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – 3x + 2;

b) x² + 7x + 6.

Lời giải:

a) x² – 3x + 2

= x² ‒ 2x ‒ x + 2

= (x² – 2x) – (x – 2)

= x(x – 2) – (x – 2)

= (x ‒ 2)(x ‒ 1).

b) x² + 7x + 6

= x² + x + 6x + 6

= (x² + x) + (6x + 6)

= x(x + 1) + 6(x + 1)

= (x + 1)(x + 6).

Bài 2.24 trang 30 sách bài tập Toán 8 Tập 1: Từ một miếng bìa có dạng hình tròn (H.2.4) với bán kính R (cm), người ta khoét một hình tròn ở giữa có bán kính r (cm), r < R.

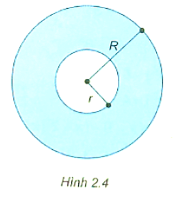
a) Viết công thức tính diện tích phần còn lại của miếng bìa.

b) Tính diện tích phần còn lại của miếng bìa biết tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm.

Lời giải:

a) Diện tích miếng bìa hình tròn có bán kính R (cm) là: πR² (cm²)

Diện tích miếng bìa hình tròn có bán kính r (cm) là: πr² (cm²)

Diện tích phần còn lại của miếng bìa là:

πR² ‒ πr² = π(R² – r²) (cm²).

b) Ta có: π(R² – r²) = π(R – r)(R + r) (*)

Do tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm nên ta có:

R + r = 10 và R ‒ r = 3

Thay vào (*) ta được: π(10 − 3)(10 + 3) = π.7.13 = 91π.

Vậy diện tích phần còn lại của miếng bìa là 91π (cm²).

Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:

SBT Toán 8 (Kết nối tri thức) Bài 9: Phân tích đa thức thành nhân tử

SBT Toán 8 (Kết nối tri thức) Bài 10: Tứ giác

SBT Toán 8 (Kết nối tri thức) Bài 11: Hình thang cân

SBT Toán 8 (Kết nối tri thức) Bài 12: Hình bình hành

SBT Toán 8 (Kết nối tri thức) Bài 13: Hình chữ nhật