Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Hàm số bậc nhất (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Hàm số bậc nhất (HAY NHẤT 2024)
1. Lý thuyết
a. Hàm số bậc nhất y = ax + b (a ≠ 0)
+) Tập xác định: D=ℝ.
+) Sự biến thiên:
Với a > 0 hàm số đồng biến trên R. Ta có bảng biến thiên:
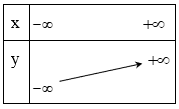
Với a < 0 hàm số nghịch biến trên R. Ta có bảng biến thiên:
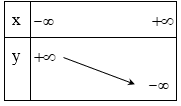
+) Đồ thị:
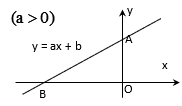
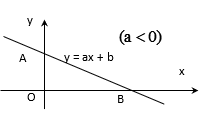
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này cắt trục tung tại điểm A(0; b) và cắt trục hoành tại điểm B(−ba;0).
b. Hàm số hằng y = b.
+) Tập xác định: D=ℝ.
+) Đồ thị:
Khi a = 0 hàm số y = ax + b trở thành hàm hằng y = b.
Đồ thị hàm số y = b là đường thẳng song song hoặc trùng với trục hoành, cắt trục tung tại điểm A(0; b). Ta gọi đường thẳng này là đường thẳng y = b.
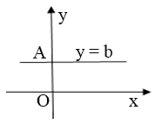
c. Hàm số y = |x|
+) Tập xác định: D=ℝ.
+) Theo định nghĩa của giá trị tuyệt đối, ta có:
y=|x|={x khi x≥0−x khi x<0.
+) Sự biến thiên:
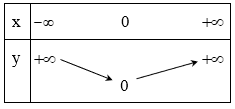
Hàm số y = |x| nghịch biến trên khoảng (−∞;0) và đồng biến trên khoảng (0;+∞).
Bảng biến thiên:
+) Đồ thị:
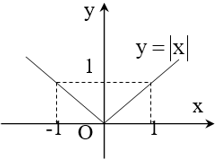
Hàm số y = |x| là hàm số chẵn nên đồ thị của nó nhận Oy làm trục đối xứng.
Trong nửa khoảng[0;+∞) đồ thị hàm số y = |x| trùng với đồ thị hàm số y = x.
Trong khoảng (−∞;0)đồ thị hàm số y = |x| trùng với đồ thị hàm số y = -x.
2. Các dạng bài tập
Dạng 2.1: Xác định hàm số y = ax + b () .
a. Phương pháp giải:
Để xác định hàm số bậc nhất ta thực hiện theo các bước sau:
+) Giả sử hàm số cần tìm có dạng y = ax + b (a≠0).
+) Dựa vào giả thiết bài toán để thiết lập hệ phương trình với ẩn a, b.
+) Giải hệ phương trình để tìm ẩn số a, b và suy ra hàm số cần tìm.
b. Ví dụ minh họa:
Ví dụ 1: Cho hàm số bậc nhất có đồ thị là đường thẳng d, tìm hàm số đó biết:
a. d đi qua điểm A(-2; 1) và B(1; -2).
b. d cắt trục tung tại điểm có tung độ là 3 và đi qua điểm M(-2; 4)
Hướng dẫn:
a. Giả sử hàm số bậc nhất cần tìm có dạng: y = ax + b (a≠0).
Đồ thị hàm số đi qua điểm A(-2; 1) và B(1; -2) nên ta có:
{1=−2a+b−2=a+b⇔{a=−1b=−1
Vậy hàm số cần tìm là: y=−x−1
b. Giả sử hàm số bậc nhất cần tìm có dạng: y = ax + b (a≠0).
Vì d cắt trục tung tại điểm có tung độ là 3 nên d đi qua A(0; 3).
Đồ thị hàm số đi qua hai điểm A(0; 3) và M(-2; 4) nên ta có:
{3=b4=−2a+b⇔{a=−12b=3
Vậy hàm số cần tìm là: y=−12x+3.
Ví dụ 2: Cho hàm số bậc nhất y = f(x). Tìm hàm số đó biết f(−1)=2 và f(2)=−3.
Hướng dẫn:
Giả sử hàm số bậc nhất cần tìm có dạng:y=f(x)=ax+b (a≠0) .
Theo đề bài, f(−1)=2 và f(2)=−3 nên ta có hệ phương trình:
{2=−a+b−3=2a+b⇔{a=−53b=13
Vậy hàm số cần tìm là: y=−53x+13
Dạng 2.2: Vị trí tương đối của hai đường thẳng.
a. Phương pháp giải:
Cho hai đường thẳng d:y=ax+b và d' Khi đó:
+) và
+)
+) và
+) Khi đó tọa độ giao điểm của hai đường thẳng là nghiệm của hệ phương trình: .
b. Ví dụ minh họa:
Ví dụ 1: Xét hàm số bậc nhất có đồ thị là đường thẳng d, hãy xác định hàm số biết rằng:
a. d đi qua điểm A(3; -2), đồng thời song song với d’: 3x - 2y + 1 = 0.
b. d đi qua B(2; -1) và vuông góc với d’: y = 4x + 3.
Hướng dẫn:
a. Giả sử hàm số bậc nhất cần tìm có dạng: .
Ta biến đổi d’ về dạng:
Do d song song d’, suy ra: (1)
Lại có d đi qua điểm A(3; -2), suy ra: -2 = 3a + b (2)
Từ (1) và (2) suy ra: .
Vậy hàm số cần tìm là: .
b. Giả sử hàm số bậc nhất cần tìm có dạng:.
Do d đi qua điểm B(2; -1) nên: -1 = 2a + b (1)
Lại có d vuông góc d’: y = 4x + 3, suy ra: (2)
Từ (1) và (2) suy ra:
Vậy hàm số cầm tìm là: .
Ví dụ 2: Cho hai đường thẳng và lần lượt có phương trình: , . Xác định vị trí tương đối của và trong trường hợp .
Hướng dẫn:
Khi ta có :
Ta có: và suy ra hai đường thẳng song song với nhau.
Dạng 2.3: Hàm số chứa dấu giá trị tuyệt đối.
a. Phương pháp giải:
Cho hàm số , ta có:
Do đó, để vẽ đồ thị của hàm số ta sẽ vẽ hai đường thẳng và rồi xóa đi phần đường thẳng nằm ở phía dưới trục hoành. Phần đường thẳng nằm phía trên trục hoành chính là đồ thị của hàm số cần tìm.
b. Ví dụ minh họa:
Ví dụ 1: Vẽ đồ thị của các hàm số sau
a.
b.
Hướng dẫn:
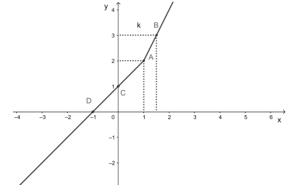
a. Đồ thị hàm số y = 2x là đường thẳng đi qua hai điểm A(1; 2) và .
Đồ thị hàm số y = x + 1 là đường thẳng đi qua hai điểm C(0; 1) và D(-1; 0).
Ta vẽ đường thẳng y = 2x với phần đồ thị sao cho hoành độ x thỏa mãn và vẽ đường thẳng y = x + 1 với phần đồ thị sao cho hoành độ x thỏa mãn x < 1.
b. Ta có:
Với đồ thị hàm số y = x - 1 là phần đường thẳng nằm phía trên trục hoành và đi qua hai điểm (1; 0); (2; 1).
Với đồ thị hàm số y = -x + 1 là phần đường thẳng nằm phía trên trục hoành và đi qua hai điểm (1; 0); (0; 1).
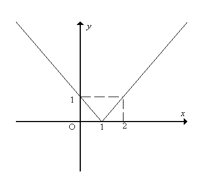
Ví dụ 2: Cho hàm số . Tìm giá trị của x để .
Hướng dẫn:
Ta có:
Vậy với x = -3 hoặc x = -7 thì f(x) = 2.
3. Bài tập vận dụng
a. Tự luận
Câu 1: Lập phương trình đường thẳng đi qua hai điểm và .
Hướng dẫn:
Giả sử phương trình đường thẳng cần tìm có dạng:
Đường thẳng đi qua hai điểm , nên ta có:
Vậy phương trình đường thẳng cần tìm là:
Câu 2: Tìm m để hàm số nghịch biến trên R.
Hướng dẫn:
Hàm số có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên R thì .
Câu 3: Tìm m để hàm số đồng biến trên R
Hướng dẫn:
Điều kiện xác định của hàm số là .
Hàm số có dạng hàm số bậc nhất nên hàm số đồng biến trên R khi . Kết hợp với điều kiện (*), ta được
Vậy với thì hàm số đã cho đồng biến trên R
Câu 4: Tìm tất cả các giá trị của m để hai đường thẳng và song song với nhau?
Hướng dẫn:
Hai đường thẳng và song song với nhau:
Câu 5: Tìm tọa độ giao điểm của hai đường thẳng và ?
Hướng dẫn:
Phương trình hoành độ giao điểm của hai đường thẳng là:
Thay vào suy ra .
Vậy tọa độ giao điểm của hai đường thẳng là .
Câu 6: Tìm m để ba đường thẳng , , đồng quy.
Hướng dẫn:
Gọi A là giao điểm của hai đường thẳng và . Khi đó tọa độ điểm A là nghiệm của hệ phương trình:
Suy ra .
Để đồng quy thì . Do đó, ta có:
Câu 7: Đồ thị hàm số y = 3x + 2 cắt hai trục Ox, Oy lần lượt tại hai điểm A và B. Tính diện tích tam giác OAB.
Hướng dẫn:
Giao điểm của đồ thị hàm số với trục Ox là: . Do đó
Giao điểm của đồ thị hàm số với trục Oy là: . Do đó
Diện tích tam giác là: .
Câu 8: Cho hàm số . Trên đồ thị của hàm số lấy hai điểm A và B có hoành độ lần lượt là -2 và 1. Hãy xác định phương trình đường thẳng AB.
Hướng dẫn:
Khi:
Khi
Phương trình đường thẳng AB có dạng:
Từ (1) và (2) suy ra:
Vậy phương trình đường thẳng AB là:
Câu 9: Vẽ đồ thị hàm số
Hướng dẫn:
Suy ra đồ thị hàm số là sự kết hợp giữa đồ thị hàm số (ứng với phần đồ thị khi ) và đồ thị hàm số (ứng với phần đồ thị khi ).
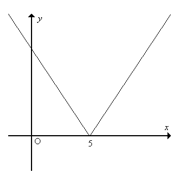
Câu 10: Đồ thị sau đây biểu diễn hàm số nào?
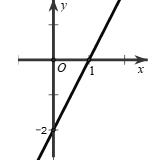
Hướng dẫn:
Giả sử hàm số cần tìm có dạng:
Đồ thị hàm số đi qua hai điểm nên ta có:
Vậy hàm số cần tìm là:
b. Trắc nghiệm
Câu 1 Cho hàm số . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến khi a >0
B. Hàm số đồng biến khi a <0
C. Hàm số đồng biến khi
D. Hàm số đồng biến khi
Hướng dẫn:
Chọn A.
Hàm số bậc nhất đồng biến khi a >0
Câu 2: Đồ thị của hàm số là hình nào dưới đây?
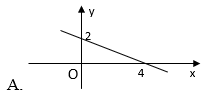
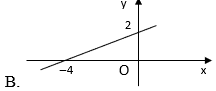
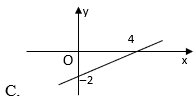
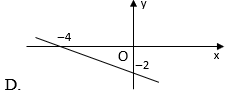
Hướng dẫn:
Chọn A.
Cho Đồ thị hàm số đi qua hai điểm .
Câu 3: Trong các hàm số sau, hàm số nào nghịch biến trên R
A.
B. y = 2
C.
D. y = 2x + 3.
Hướng dẫn:
Chọn C.
Chỉ có hàm số có hệ số nên hàm số nghịch biến trên R.
Câu 4: Cho hai đường thẳng và . Có bao nhiêu giá trị của tham số m để hai đường thẳng song song với nhau?
A. 0.
B. 1.
C. 2.
D. Vô số.
Hướng dẫn:
Chọn B.
(d) // (d’) khi và chỉ khi :
Vậy có 1 giá trị của tham số m để hai đường thẳng song song với nhau.
Câu 5: Cho hai đường thẳng và . Mệnh đề nào sau đây đúng?
A. và trùng nhau.
B. và cắt nhau và không vuông góc.
C. và song song với nhau.
D. và vuông góc với nhau.
Hướng dẫn:
Chọn B.
Ta có: suy ra hai đường thẳng cắt nhau.
Do nên hai đường thẳng không vuông góc.
Câu 6: Phương trình đường thẳng đi qua hai điểm A(5; 2) và B(-3; 2) là:
A. y = 5.
B. y = -3.
C. y = 5x + 2.
D. y = 2.
Hướng dẫn:
Chọn D.
Giả sử phương trình đường thẳng có dạng:
Đường thẳng đi qua hai điểm A(5; 2) và B(-3; 2) nên ta có:
Vậy phương trình đường thẳng cần tìm là: y = 2.
Câu 7: Đồ thị hàm số nào sau đây song song với trục hoành?
A. y = 4x - 1.
B. y = 5 - 2x.
C. y = -2.
D. x = 2.
Hướng dẫn:
Chọn C.
y = -2 là hàm hằng, đồ thị có tính chất song song với trục hoành.
Câu 8: Hàm số bằng hàm số nào sau đây?
A.
B.
C.
D.
Hướng dẫn:
Chọn D.
Câu 9: Hàm số bằng hàm số nào dưới đây?
A.
B.
C.
D.
Hướng dẫn:
Chọn C.
Câu 10: Cho hàm số có đồ thị là hình dưới đây. Giá trị của a và b là:
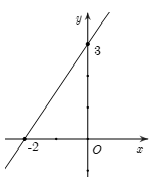
A. và .
B. và .
C. và .
D. và .
Hướng dẫn :
Chọn D.
Đồ thị hàm số đi qua hai điểm nên ta có:
4. Bài tập tự luyện
Bài 1: Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết:
a) d đi qua A(1; 1), B (3; -2)
b) d đi qua C (2; -2) và song song với Δ: x - y + 1 = 0
c) d đi qua M(1; 2) và cắt hai tia Ox, Oy tại P, Q sao cho tam giác OPQ cân tại O.
d) d đi qua N(1; -1) và d ⊥ d' với d':y = -x + 3.
Bài 2: Tìm m để ba đường thẳng d: y = 2x,d': y = -x + 6,
d": y = m2x + 5m + 3 phân biệt đồng quy.
Bài 3: Cho đồ thị hàm số có đồ thị (C) (hình vẽ)
a) Hãy lập bảng biến thiên của hàm số trên [-3;3]
b) Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên [-2;2]
Bài 4: Vẽ đồ thị hàm số y = 2x - 3. Từ đó suy ra đồ thị của:
(C1 ): y = 2|x| - 3
(C2 ): y = |2x - 3|
(C3 ): y = |2|x| - 3|
Bài 5: a) Lập bảng biến thiên của hàm số:
b) Biện luận số giao điểm của đồ thị hàm số trên với đường thẳng y = m theo m.
Bài 6: Cho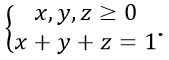
0 ≤ xy + yz + zx - 2xyz ≤ 7/27
Bài 7: Chứng minh rằng với ∀ m ≤ 1 thì x2 - 2(3m-1)x + m + 3 ≥ 0 ∀ x ∈ [1;+∞)
Bài 1: Gọi hàm số cần tìm là y = ax + b, a ≠ 0
a) Vì A ∈ d,B ∈ d nên ta có hệ phương trình:
b) Ta có Δ:y = x + 1. Vì d // Δ nên
Mặt khác C ∈ d ⇒ -2 = 2a + b ⇒ b = -4
Vậy hàm số cần tìm là y = x – 4.
c) Đường thẳng d cắt tia Ox tại P(-b/a; 0) và cắt tia Oy tại Q(0; b) với a < 0; b > 0.
Tam giác OPQ cân tại O ⇔ OP = OQ
Ta có: M ∈ d ⇒ 2 = a + b ⇒ b = 3
Vậy hàm số cần tìm là y = -x + 3.
d) Đường thẳng d đi qua N (1; -1) nên -1 = a + b
Và d ⊥ d' ⇒ a = 1 suy ra b = -2.
Vậy hàm số cần tìm là y = x – 2.
Bài 2: Tọa độ giao điểm (nếu có) của hai đường thẳng d, d’ là nghiệm của hệ phương trình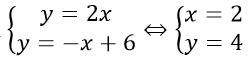
Vì ba đường thẳng d, d’, d’’ đồng quy nên M ∈ d" ta có:
4 = 2m2 + 5m + 3 ⇔ 2m2 + 5m - 1 = 0
⇔
Dễ thấy với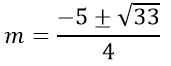
Vậy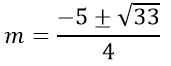
Bài 3:
a) Bảng biến thiên của hàm số trên [-3; 3]
b) Dựa vào đồ thị hàm số đã cho ta có:
Bài 4: Đồ thị hàm số y = 2x – 3 đi qua A(0; -3), B (2; 1) ta gọi là (C)
+ Khi đó đồ thị hàm số (C1 ): y = 2|x| - 3 là phần được xác định như sau
Ta giữ nguyên đồ thị (C) ở bên phải trục tung; lấy đối xứng đồ thị (C) ở phần bên phải trục tung qua trục tung.
+ (C2 ): y = |2x - 3| là phần đồ thị (C) nằm phía trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của(C).
+ (C3 ): y = |2|x| - 3| là phần đồ thị (C1 ) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của (C1 ).
Bài 5:
a) Ta có
Bảng biến thiên:
b) Dựa vào bảng biến thiên của hàm số: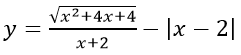
Với m > 1 thì có không giao điểm
Với m = 1 thì có một giao điểm
Với -5 < m < 1 thì có hai giao điểm
Với m < -5 thì có một giao điểm.
Bài 6: Từ giả thiết ta có x,y,z ∈ [0;1]
⇒ xy + yz + zx - 2xyz = xy + yz(1-x) + zx(1-y) ≥ 0
Cũng từ giả thiết ta suy ra:
Mặt khác ta lại có
xy + yz + zx - 2xyz ≤ 7/27 ⇔ f(yz) = (1-2x)yz + x(1-x) - 7/27 ≤ 0 (2)
Khi đó ta thấy rằng
Nếu x = 1/2 khi đó BĐT (2) thành (-1)/108 (hiển nhiên đúng).
Nếu x ≠ 1/2 thì f(yz) là hàm số bậc nhất. Do đó để chứng minh f(yz) ≤ 0 ta chỉ cần
Vậy f(yz) ≤ 0, ta có điều phải chứng minh.
Bài 7:
Ta có x2 - 2(3m-1)x + m + 3 ≥ 0
⇔ f(m) = (-6x+1)m + x2 + 2x + 3 ≥ 0
Ta thấy f(m) là hàm số bậc nhất có hệ số của m là -6x + 1 < 0 (do x ∈ [1;+∞)). Khi đó: f(m) là hàm nghịch biến ⇒ f(m) ≥ f(1) với ∀ m ≤ 1. Tức là ta có :
x2 - 2(3m-1)x + m + 3 ≥ (x-2)2 ≥ 0 (đúng với ∀ x ∈ [1;+∞)).
Xem thêm các dạng Toán 10 hay, chọn lọc khác:
Hàm số lớp 10 và cách giải các dạng bài tập
Hàm số bậc hai lớp 10 và cách giải các dạng bài tập
Cách xét tính đồng biến, nghịch biến của hàm số chi tiết
Cách xét tính chẵn, lẻ của hàm số chi tiết
Tất tần tật công thức về Hàm số y = |x|
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.