Toptailieu.vn biên soạn và giới thiệu Cách xét tính đồng biến, nghịch biến của hàm số (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Cách xét tính đồng biến, nghịch biến của hàm số (HAY NHẤT 2024)
I. Lí thuyết tổng hợp
- Cho K là một khoảng hoặc một đoạn hoặc nửa khoảng, y = f(x) là hàm số xác định trên K.
+ Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi x thuộc K thì khi x tăng f(x) cùng tăng, khi x giảm f(x) cùng giảm.
+ Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi x thuộc K thì khi x tăng f(x) giảm, khi x giảm f(x) tăng.
- Lưu ý.
+ Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi lên.
+ Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi xuống.
+ Hàm số bậc nhất y = ax + b luôn đồng biến hoặc nghịch biến trên .
II. Các công thức
- Cho hàm số y = f(x) xác định trên K. Lấy và .
Đặt T = . Ta có:
T > 0 Hàm số y = f(x) đồng biến (tăng) trên K
T < 0 Hàm số y = f(x) nghịch biến (giảm) trên K
- Cho hàm số y = f(x) xác định trên K. Lấy và .
Đặt . Ta có:
T > 0 Hàm số y = f(x) đồng biến (tăng) trên K
T < 0 Hàm số y = f(x) nghịch biến (giảm) trên K
- Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi lên.
- Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi xuống.
III. Ví dụ minh họa
Bài 1: Xét tính đồng biến, nghịch biến của hàm số trên khoảng .
Lời giải:
- Điều kiện xác định của hàm số là:
Tập xác định của hàm số y = f(x) là:
Hàm số xác định trên khoảng
- Lấy và . Đặt
Ta thấy trong khoảng thì T luôn xác định.
Với
Hàm số đồng biến trên khoảng .
Bài 2: Xét tính đồng biến, nghịch biến của hàm số: trên khoảng .
Lời giải:
Hàm số xác định trên R
Hàm số xác định trên khoảng
Lấy và
(1)
Ta có:
(2)
Từ (1) và (2) Hàm số nghịch biến trên khoảng
Bài 3: Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Xét tính đồng biến, nghịch biến của hàm số trên khoảng (2; 4) và đoạn [-4; -2].
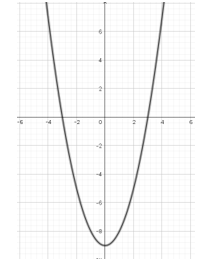
Lời giải:
Ta thấy khi thì đồ thị của hàm số y = f(x) đi lên
Hàm số y = f(x) đồng biến trên khoảng (2; 4)
Ta thấy khi thì đồ thị của hàm số y = f(x) đi xuống
Hàm số y = f(x) nghịch biến trên đoạn [-4; -2]
IV. Bài tập tự luyện
Bài 1: Xét tính đồng biến, nghịch biến của hàm số y = f(x) = 4x – 9 trên toàn tập xác định của nó.
Bài 2: Xét tính đồng biến, nghịch biến của hàm số trên các khoảng và .
Bài 3: Cho hàm số y = x3 - x2 + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R
Bài 4: Cho hàm số
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
Bài 5: Tìm tất cả các giá trị của tham số m sao cho hàm số
Bài 6: Cho hàm số y = x3 + 3x2 + mx + 1 - 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Bài 7: Hỏi hàm số
đồng biến trên các khoảng nào?
Bài 8: Tìm khoảng đồng biến của hàm số y = 2x3 - 9x3 + 12x + 3
Bài 9: Khoảng nghịch biến của hàm số y = x4 - 2x2 - 1 là:
Bài 10: Cho hàm số
Khẳng định nào sau đây là khẳng định đúng?
Bài 11: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x
Bài 12: Hàm số: 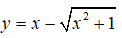
Bài 13: Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [; ] và các hàm số y = |x| trên khoảng (-∞; +∞).
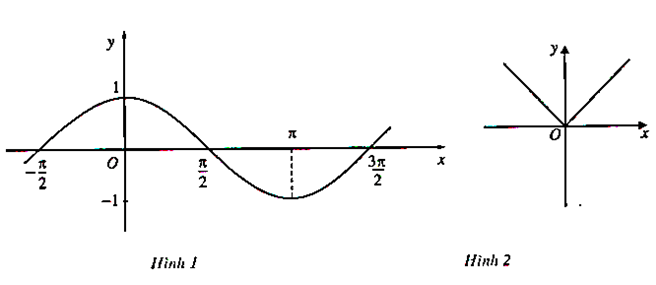
Bài 14: Xét các hàm số sau và đồ thị của chúng:
a) y = - (H.4a) b) y = (H.4b)
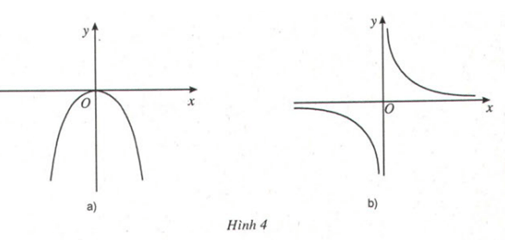
Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng.
Bài 15: Khẳng định ngược lại với định lí trên có đúng không ? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không ?
Bài 16: Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x2
b) y = .x3 + 3x2 - 7x -2
c) y = x4 - 2x2 + 3
d) y = -x3 + x2 – 5
Bài 17: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
Bài 18: Cho hàm số y = -x3 + 3x2 + 3mx - 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
Bài 19: Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- ; ]
Bài 20: Chứng minh rằng hàm số đồng biến trên khoảng (0;1) và nghịch biến trên khoảng (1,2).
Xem thêm các dạng Toán 10 hay, chọn lọc khác:
Hàm số lớp 10 và cách giải các dạng bài tập
Hàm số bậc nhất lớp 10 và cách giải các dạng bài tập
Hàm số bậc hai lớp 10 và cách giải các dạng bài tập
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.