Toptailieu.vn biên soạn và giới thiệu Công thức giải hệ phương trình bậc nhất hai ẩn, ba ẩn (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức giải hệ phương trình bậc nhất hai ẩn, ba ẩn (50 bài tập minh họa) HAY NHẤT 2024

I. Lí thuyết tổng hợp

1. Hệ phương trình bậc nhất hai ẩn

- Hệ phương trình bậc nhất hai ẩn có dạng tổng quát: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2\end{array}\right.$ ($a_1,b_1$ không đồng thời bằng 0, $a_2,b_2$ không đồng thời bằng 0).

- Nghiệm của hệ phương trình bậc nhất hai ẩn là cặp số (x; y) sao cho x và y đồng thời là nghiệm của cả hai phương trình của hệ.

2. Hệ phương trình bậc nhất ba ẩn

- Hệ phương trình bậc nhất ba ẩn có dạng tổng quát: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array}\right.$( trong đó $a_1,b_1,c_1$  không đồng thời bằng 0,$a_2,b_2,c_2$ không đồng thời bằng 0 và $a_3,b_3,c_3$ không đồng thời bằng 0).

- Nghiệm của hệ phương trình bậc nhất ba ẩn là bộ ba số (x; y; z) sao cho x, y và z đồng thời là nghiệm của cả ba phương trình của hệ.

3. Phương pháp giải

- Muốn giải hệ phương trình bậc nhất hai ẩn, ba ẩn ta thường dùng:

+ Phương pháp thế: Rút một ẩn theo ẩn còn lại trong một phương trình của hệ và thế vào phương trình còn lại, thu được hệ mới mà trong đó có một phương trình một ẩn. Giải phương trình một ẩn vừa có rồi suy ra nghiệm của hệ.

+ Phương pháp cộng đại số: Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong các phương trình bằng nhau hoặc đối nhau. Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0. Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

- Tổng quát: Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để quy về giải hệ phương trình có ít ẩn số hơn.

Để khử bớt ẩn, ta cũng có thể dùng các phương pháp cộng đại số hay phương pháp thế giống như đối với hệ phương trình bậc nhất hai ẩn.

II. Các công thức

- Hệ phương trình bậc nhất hai ẩn có dạng: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2\end{array}\right.$ với $a_1,b_1$ không đồng thời bằng 0, $a_2,b_2,c_2$ đều khác 0. Ta có:

+ Hệ phương trình có nghiệm duy nhất khi  $\frac{a_1}{a_2}\ne \frac{b_1}{b_2}$

+ Hệ phương trình vô nghiệm khi $\frac{a_1}{a_2}=\frac{b_1}{b_2}\ne \frac{c_1}{c_2}$

+ Hệ phương trình có vô số nghiệm khi $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$

- Phương pháp thế: (với điều kiện các phương trình có nghĩa)

$$\begin{gathered} \left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2\end{array}\right. \\ \iff \left\{\begin{array}{l}y=\frac{c_1-a_{1}x}{b_1}\\ a_{2}x+b_{2}y=c_2\end{array}\right. \\ \iff \left\{\begin{array}{l}y=\frac{c_1-a_{1}x}{b_1}\\ a_{2}x+b_2\left(\frac{c_1-a_{1}x}{b_1}\right)=c_2\end{array}\right. \end{gathered}$$

- Phương pháp cộng đại số:

a. Quy tắc cộng đại số

Gồm hai bước:

+ Bước 1: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới.

+ Bước 2: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia).

b. Tóm tắt cách giải hệ phương trình bằng phương pháp cộng đại số

+ Bước 1: Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

+ Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).

+ Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

III. Ví dụ minh họa

Bài 1: Cho hệ phương trình $\left\{\begin{array}{l}2mx+3y=m\\ 4x+6y=10\end{array}\right.$. Tìm m thỏa mãn các yêu cầu sau:

a) Hệ phương trình có nghiệm duy nhất;

b) Hệ phương trình có vô số nghiệm;

c) Hệ phương trình vô nghiệm.

Lời giải:

a)

Hệ phương trình đã cho có nghiệm duy nhất

$$\begin{gathered} \iff \frac{2m}{4}\ne \frac{3}{6} \\ \iff \frac{m}{2}\ne \frac{1}{2}\iff m\ne 1 \end{gathered}$$

Vậy khi $m\ne 1$ thì hệ phương trình đã cho có nghiệm duy nhất.

b)

Hệ phương trình đã cho có vô số nghiệm

$$\begin{gathered} \iff \left\{\begin{array}{l}\frac{2m}{4}=\frac{3}{6}\\ \frac{3}{6}=\frac{m}{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}m=1\\ m=5\end{array}\right.\iff m\in \varnothing \end{gathered}$$

Vậy không tồn tại m để hệ đã cho có vô số nghiệm.

c)

Hệ phương trình đã cho vô nghiệm

$$\begin{gathered} \iff \left\{\begin{array}{l}\frac{2m}{4}=\frac{3}{6}\\ \frac{3}{6}\ne \frac{m}{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}m=1\\ m\ne 5\end{array}\right.\iff m=1 \end{gathered}$$

Vậy khi m = 1 thì hệ đã cho vô nghiệm.

Bài 2: Giải hệ phương trình $\left\{\begin{array}{l}3x+y=4\\ 2x-3y=5\end{array}\right.$ theo hai cách.

Lời giải:

Cách 1:

$$\begin{gathered} \left\{\begin{array}{l}3x+y=4\\ 2x-3y=5\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3x\\ 2x-3y=5\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3x\\ 2x-3(4-3x)=5\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3x\\ 2x-12+9x=5\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3x\\ 11x=17\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3x\\ x=\frac{17}{11}\end{array}\right. \\ \iff \left\{\begin{array}{l}y=4-3.\frac{17}{11}\\ x=\frac{17}{11}\end{array}\right. \\ \iff \left\{\begin{array}{l}y=\frac{-7}{11}\\ x=\frac{17}{11}\end{array}\right. \end{gathered}$$

Vậy nghiệm của hệ phương trình là $\left(x;y\right)=\left(\frac{17}{11};\frac{-7}{11}\right)$.

Cách 2:

$$\begin{gathered} \left\{\begin{array}{l}3x+y=4\\ 2x-3y=5\end{array}\right. \\ \iff \left\{\begin{array}{l}(-2).3x+(-2).y=(-2).4\\ 3.2x-3.3y=3.5\end{array}\right. \\ \iff \left\{\begin{array}{l}-6x-2y=-8\\ 6x-9y=15\end{array}\right. \\ \iff \left\{\begin{array}{l}-6x-2y=-8\\ -11y=7\end{array}\right. \\ \iff \left\{\begin{array}{l}-6x-2y=-8\\ y=\frac{-7}{11}\end{array}\right. \\ \iff \left\{\begin{array}{l}-6x-2.\frac{-7}{11}=-8\\ y=\frac{-7}{11}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{17}{11}\\ y=\frac{-7}{11}\end{array}\right. \end{gathered}$$

Vậy nghiệm của hệ phương trình là $\left(x;y\right)=\left(\frac{17}{11};\frac{-7}{11}\right)$.

Bài 3: Giải hệ phương trình $\left\{\begin{array}{l}x+2y+z=3\\ x+4y=2\\ y-z=1\end{array}\right.$.

Lời giải:

Ta có: $\left\{\begin{array}{l}x+2y+z=3\\ x+4y=2\\ y-z=1\end{array}\right.$

$\iff \left\{\begin{array}{l}2y-z=-1\\ x+4y=2\\ y-z=1\end{array}\right.$ (Lấy PT (2) trừ vế theo vế  PT (1))

$\iff \left\{\begin{array}{l}2(1+z)-z=-1\\ x+4y=2\\ y=1+z\end{array}\right.$(Thế từ PT (3) vào PT (1))

$$\begin{gathered} \iff \left\{\begin{array}{l}2+2z-z=-1\\ x+4y=2\\ y=1+z\end{array}\right. \\ \iff \left\{\begin{array}{l}z=-3\\ x+4y=2\\ y=1+z\end{array}\right. \\ \iff \left\{\begin{array}{l}z=-3\\ x+4y=2\\ y=-2\end{array}\right. \\ \iff \left\{\begin{array}{l}z=-3\\ x+4.(-2)=2\\ y=-2\end{array}\right. \\ \iff \left\{\begin{array}{l}z=-3\\ x=10\\ y=-2\end{array}\right. \end{gathered}$$

Vậy nghiệm của hệ phương trình là (x; y; z) = {10; -2; -3}.

IV. Bài tập vận dụng 

Bài 1: Giải hệ phương trình: $\left\{\begin{array}{l}x+3y=5\\ 2x-7y=6\end{array}\right.$ 

Bài 2: Giải hệ phương trình: $\left\{\begin{array}{l}x+3y+z=9\\ 2x-7y=6\\ x-z=3\end{array}\right.$

Bài 3: Cho hệ phương trình 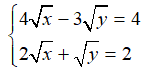. Biết nghiệm của hệ phương trình (x; y) , tính x.y

Bài 4: Giải hệ phương trình:

Bài 5: Giải hệ phương trình:

Bài 6: Cho hệ phương trình 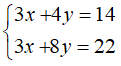. Tính x² + y²

Bài 7: Giải hệ phương trình:

Bài 8: Giải hệ phương trình

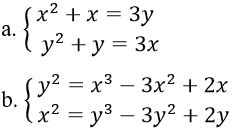
Bài 9: Giải hệ phương trình

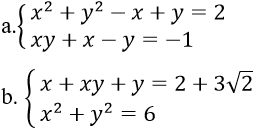
Bài 10: Xác định m để hệ phương trình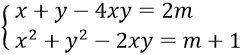có nghiệm

V. Bài tập tự luyện

Câu 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?

A.$\left\{\begin{array}{l}x+3y\ge 0\\ 2x\le 0\end{array}\right.$

B.$\left\{\begin{array}{l}{x}^2+3y\ge 2\\ 2x+y\le -1\end{array}\right.$

C.$\left\{\begin{array}{l}4x+3y-1\ge 0\\ x+y^3>0\end{array}\right.$

D. $\left\{\begin{array}{l}-x^2+3y\ge 5\\ x+y^3\le 1\end{array}\right.$

Câu 2. Trong các khẳng định sau, khẳng định nào đúng?

A. Điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

B. Điểm M(1 ; 0) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

C. Điểm N(0 ; –1) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

D. Điểm P(1 ; 1) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

Câu 3. Tìm khẳng định sai trong các khẳng định sau:

A. Hệ $\left\{\begin{array}{l}x+y\ge -1\\ y^2-1\le 0\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn;

B. Hệ $\left\{\begin{array}{l}x\ge 1+y\\ 5x+y<0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

C. Hệ $\left\{\begin{array}{l}x+1+y>0\\ x^2+y<0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

D. Hệ $\left\{\begin{array}{l}\frac{1}{2}x+2y<7\\ x+3y\le 0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

Câu 4. Cho hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. M(0; 1);

B. N(–1; 1);

C. P(–1; 4);

D. Q(1; 3).

Câu 5. Cho hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$. Và các điểm sau: M(–1 ; 2), N(0; –1), O(0; 0). Có mấy điểm thuộc miền nghiệm của hệ bất phương trình đã cho?

A. 0;

B. 1;

C. 2;

D. 3.

Câu 6. Cặp số (0; –3) là nghiệm của hệ bất phương trình nào sau đây?

A. $\left\{\begin{array}{l}x-y\le 1\\ x+3y\le 3x-4\end{array}\right.$

B. $\left\{\begin{array}{l}2x-y>0\\ 2x+y>1\end{array}\right.$

C. $\left\{\begin{array}{l}-x-4y>-3\\ 2x+y\le 2\end{array}\right.$

D. $\left\{\begin{array}{l}2x-y\le -3\\ 5y\ge -1\end{array}\right.$

Câu 7. Cho hai điểm M(1; 0) và N(–2; –1) và hệ bất phương trình $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$. Trong hai điểm M và N, điểm nào thuộc miền nghiệm của hệ đã cho?

A. Cả M và N đều không thuộc miền nghiệm của hệ đã cho.

B. Điểm M thuộc miền nghiệm còn N không thuộc miền nghiệm của hệ đã cho.

C. Điểm M không thuộc miền nghiệm còn N thuộc miền nghiệm của hệ đã cho.

D. Cả hai điểm M và N đều thuộc miền nghiệm của hệ đã cho.

Câu 8. Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y<0\\ x+3y>-1\\ x+y<3\end{array}\right.$ là miền không gạch chéo (không kể bờ) của hình vẽ nào trong các hình vẽ sau?

A.

B.

C.

D.

Câu 9. Miền không gạch chéo trong hình vẽ dưới đây (không chứa bờ), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?

A. $\left\{\begin{array}{l}x-y\ge -2\\ 2x-y\ge 1\end{array}\right.$

B. $\left\{\begin{array}{l}x-y>-2\\ 2x-y<1\end{array}\right.$

C. $\left\{\begin{array}{l}x-y<-2\\ 2x-y>1\end{array}\right.$

D. $\left\{\begin{array}{l}x-y<-2\\ 2x-y<1\end{array}\right.$

Câu 10. Giá trị nhỏ nhất F_min của biểu thức F= –x + y trên miền xác định bởi hệ $\left\{\begin{array}{c}-2x+y\ge 2\\ y-x\le 4\\ x+2y\ge 5\end{array}\right.$ là:

A. F_min = $\frac{11}{5}$;

B. F_min = 0;

C. F_min = 2;

D. F_min = 4.

Câu 11. Biểu thức F = 2x + y đạt giá trị nhỏ nhất với điều kiện $\left\{\begin{array}{c}2x-y\le 2\\ x-2y\le 2\\ y\ge 0\\ x\ge 0\end{array}\right.$ tại điểm có toạ độ là:

A. (0; 0);

B. ($\frac{2}{3}$; $\frac{-2}{3}$);

C. (0; –1);

D. (1; 0).

Câu 12. Một người nông dân dự định quy hoạch x sào đất trồng rau cải và y sào đất trồng cà chua. Biết rằng người nông dân chỉ có tối đa 900 nghìn đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng rau cải là 100 nghìn đồng, mỗi sào đất trồng cà chua là 50 nghìn đồng. Trong các hệ bất phương trình sau, hệ nào mô tả các ràng buộc đối với x, y ?

A. $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 900\end{array}\right.$;

B. $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y\le 18\end{array}\right.$;

C. $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 2x+y>18\end{array}\right.$;

D. $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+2y\le 18\end{array}\right.$.

Câu 13. Cho hệ $\left\{\begin{array}{l}x+y\le 1\\ 4x-y\le 2\\ x\ge 0\end{array}\right.$. Giá trị lớn nhất của biểu thức P = x – y trên miền nghiệm của hệ đã cho là:

A. – 1;

B. $\frac{1}{5}$;

C. 2;

D. 1

Câu 14. Cho hệ bất phương trình $\left\{\begin{array}{l}x-y>1\\ \frac{1}{3}X-y\le 2\end{array}\right.$ có tập nghiệm là S. Trong các khẳng định sau, khẳng định nào đúng?

A. (0; 1) ∈ S;

B. (0; –1) ∉ S;

C.$\left(\frac{1}{3};1\right)$ ∈ S;

D. $\left(-\frac{1}{3};1\right)$ ∉ S.

Xem các Phương pháp giải bài tập hay, chi tiết khác: 

Bất đẳng thức lớp 10 và cách giải bài tập

Bất phương trình bậc nhất và cách giải bài tập

Bất phương trình bậc hai và cách giải bài tập

Hệ bất phương trình bậc nhất một ẩn và cách giải bài tập

Các tính chất của bất đẳng thức lớp 10 đầy đủ, chi tiết