Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Số trung bình cộng. Số trung vị. Mốt (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Số trung bình cộng. Số trung vị. Mốt (HAY NHẤT 2024)
A. Lí thuyết
1. Số trung bình cộng
Ta có thể tính số trung bình cộng của các số liệu thống kê theo các công thức:
+ Với bảng phân bố tần số và tần suất: , lần lượt là tần số, tần suất của giá trị , n là số các số liệu thống kê. Ta có số trung bình cộng:
+ Với bảng phân bố tần số và tần suất ghép lớp: , , lần lượt là giá trị đại diện, tần số, tần suất của lớp thứ i, n là số các số liệu thống kê. Ta có số trung bình cộng:
2. Số trung vị
Khi ta sắp thứ tự các số liệu thống kê thành dãy không giảm (hoặc không tăng). Số trung vị (của các số liệu thống kê đã cho), kí hiệu là , là số đứng giữa dãy nếu số phần tử là lẻ và là trung bình cộng của hai số đứng giữa dãy nếu số phần tử là chẵn.
3. Mốt
Mốt của một bảng phân bố tần số là giá trị có tần số lớn nhất và được kí hiệu là .
B. Các dạng toán và phương pháp giải
Dạng 1. Tính số trung bình cộng
Phương pháp giải:
+ Với bảng phân bố tần số, tần suất:
Số trung bình cộng:
+ Với bảng phân bố tần số, tần suất ghép lớp:
Số trung bình cộng:
Ví dụ: Trong một trường THPT, để tìm hiểu tình hình học môn Toán của lớp 10A, người ta cho hai lớp thi Toán theo cùng một đề và lập được bảng phân bố tần số:
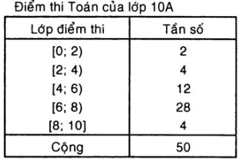
Hãy tính số trung bình cộng của bảng phân bố.
Lời giải:
Trung bình cộng các điểm thi Toán của lớp 10A là:
Vậy trung bình cộng của điểm thi Toán lớp 10A là 6,12.
Dạng 2: Tìm số trung vị
Phương pháp giải:
+ Sắp xếp thứ tự các số liệu thống kê theo thứ tự không giảm.
+ Nếu có n số liệu, n = 2k + 1 thì
+ Nếu có n số liệu, n = 2k thì
Ví dụ: Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch là: 650; 840; 690; 2500; 720; 670; 3000. (đơn vị: nghìn đồng). Tìm số trung vị của các số liệu thống kê đã cho. Nêu ý nghĩa của kết quả đã tìm được.
Lời giải:
Sắp xếp thứ tự các số liệu thống kê, ta thu được dãy tăng các số liệu sau: 650; 670; 690; 720; 840; 2500; 3000 (nghìn đồng)
Ta có số các số liệu thống kê là n = 7 = 2.3 + 1
Số trung vị là
Số các số liệu thống kê quá ít (n = 7 < 10), do đó không nên chọn số trung bình cộng làm đại diện cho các số liệu đã cho. Trong trường hợp này ta chọn số trung vị làm đại diện cho tiền lương hàng tháng của mỗi người trong 7 nhân viên được khảo sát.
Dạng 3. Tìm Mốt
Phương pháp giải:
Trong bảng phân bố tần số, giá trị có tần số lớn nhất được gọi là mốt của bảng phân bố kí hiệu .
Ví dụ: Điều tra tiền lương hàng tháng của 30 công nhân của một xưởng may, ta có bảng phân bố tần số như sau:

Hãy tính số trung bình cộng, mốt của bảng phân bố trên.
Lời giải:
Số trung bình cộng tiền lương hàng tháng của công nhân là:
(nghìn đồng)
Bảng phân bố đã cho có hai giá trị có tần số bằng nhau và lớn hơn tần số của những giá trị khác là 700 và 900. Trong trường hợp này ta xem rằng có hai mốt là và
C. Bài tập vận dụng
Bài 1: Cho biết tình hình thu hoạch lúa vụ mùa năm 1980 của ba hợp tác xã ở địa phương V như sau:
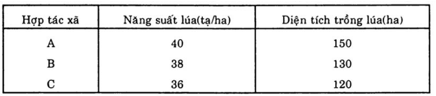
Hãy tính năng suất lúa trung bình của vụ mùa năm 1980 trong ba hợp tác xã trên.
Đáp án: 38,15 tạ/ha
Bài 2: Có 100 học sinh tham dự kì thi học sinh giỏi toán (thang điểm 20). Kết quả được cho trong bảng sau đây:
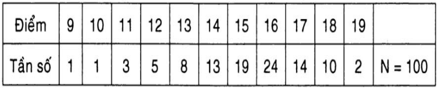
Hãy tính số trung bình và mốt của bảng số liệu trên.
Đáp án: ,
Bài 3: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau (đơn vị mm).
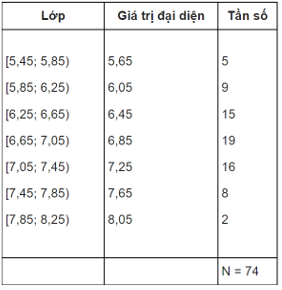
Hãy tính chiều dài trung bình của 74 chiếc lá.
Đáp án: 6,8 (mm)
Bài 4: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89. Tính điểm trung bình, mốt, số trung vị của số liệu.
Đáp án: , ,
Bài 5: Điểm thi toán của 9 học sinh như sau: 1; 6; 7; 3; 1; 8; 9; 8; 10. Tìm số trung vị của số liệu.
Đáp án: 7
Bài 6: Điểm thi lại của 4 học sinh môn Ma trận như sau: 1; 2,5; 8; 9,5. Tìm số trung vị của số liệu.
Đáp án: 5,25
Bài 7: Một cửa hàng bán 6 loại quạt với giá tiền là 100, 150, 300, 350, 400, 500 (nghìn đồng). Số quạt cửa hàng bán ra trong mùa hè vừa qua được thống kê trong bảng tần số sau:
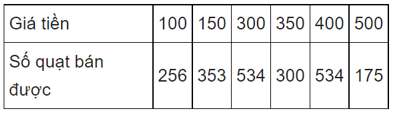
Tìm mốt của số liệu.
Đáp án: và
Bài 8: Tìm mốt của bảng số liệu sau:

Đáp án:
Bài 9: điểm thi HKI môn toán của tổ học sinh lớp 10C ( quy ước làm tròn đến 0,5 điểm) liệt kê như sau: 2; 5; 7,5; 8; 5; 7; 6,5; 9; 4,5; 10.
Tính điểm trung bình của 10 học sinh đó ( quy tròn đến chữ thập phân thứ nhất)
Đáp án:
Điểm trung bình của 10 HS là
Bài 10: Thu nhập gia đình/năm của hai nhóm dân cư ở hai xã của một huyện được cho trong bảng sau: (đv: triệu đồng)
|
Thu nhập/năm |
Số gia đình |
|
|
Lớp |
Nhóm 1 |
Nhóm 2 |
a) Tìm số trung bình của thu nhập gia đình/năm của nhóm 1
b) Tìm số trung bình của thu nhập gia đình/năm của nhóm 2
c) Hỏi nhóm nào có thu nhập cao hơn
Đáp án:
a) Số trung bình của thu nhập gia đình/năm của nhóm 1
b) Số trung bình thu nhập gia đình/năm của nhóm 2
c) So sánh thu nhập trung bình của hai nhóm: nhóm 2 có thu nhập cao hơn.
D. Bài tập tự luyện
Câu 1:
Thống kê một điểm kiểm tra 45 phút của 40 học sinh của một lớp 10 năm học 2017 - 2018 cho ta kết quả như sau:
|
3 |
5 |
7 |
9 |
10 |
6 |
8 |
3 |
4 |
6 |
5 |
7 |
8 |
10 |
|
9 |
3 |
6 |
4 |
7 |
8 |
9 |
10 |
6 |
9 |
7 |
4 |
5 |
3 |
|
3 |
7 |
9 |
6 |
10 |
8 |
7 |
5 |
4 |
8 |
9 |
7 |
|
|
Chọn phát biểu sai trong các phát biểu sau:
A. Trong 40 số liệu thống kê trên, số giá trị khác nhau là 8
B. Giá trị 9 có tần số là 6
C. Giá trị 10 có tần suất là 10%
D. Giá trị 10 có tần suất là 4
Câu 2:
Cho bảng phân bố tần số sau:
|
Lớp |
[20; 25) |
[25; 30) |
[30; 35) |
[35; 40) |
[40; 45) |
Cộng |
Cộng |
|
Tần số |
2 |
7 |
15 |
8 |
3 |
35 |
a) Trong các giá trị sau đây, giá trị nào gần nhất với số trung bình của bảng số liệu trên?
A. 31,5
B. 32
C. 32,5
D. 33
b) Trong các giá trị sau đây, giá trị nào gần nhất với độ lệch chuẩn của bảng số liệu trên?
A. 4
B. 4,5
C. 5
D. 6,5
Câu 3:
Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và trình bày mẫu số liệu dưới dạng bảng phân bố tần số sau (đơn vị xen-ti-mét).
|
Lớp |
Tần số |
|
[5,45; 5,85) |
5 |
|
[5,85; 6,25) |
9 |
|
[6,25; 6,65) |
15 |
|
[6,65; 7,05) |
19 |
|
[7,05; 7,45) |
16 |
|
[7,45; 7,85) |
8 |
|
[7,85; 8,25) |
2 |
|
Cộng |
74 |
a) Trong các giá trị sau đây, giá trị nào gần nhất với số trung bình của bảng số liệu trên?
A. 6,5
B. 6,6
C. 6,7
D. 6,8
b) Trong các giá trị sau đây, giá trị nào gần nhất với độ lệch chuẩn của bảng số liệu trên?
A. 0,58
B. 0,57
C. 0,56 d. 0,55
Câu 4:
Một xạ thủ bắn 30 viên đạn vào bia kết quả được ghi lại trong bảng phân bổ tần số sau:
|
Lớp |
Tần số |
|
6 |
4 |
|
7 |
3 |
|
8 |
8 |
|
9 |
9 |
|
10 |
6 |
|
Cộng |
30 |
Khi đó điểm số trung bình cộng là (kết quả làm tròn đến hàng phần trăm):
A. 8,33
B. 8,34
C. 8,31
D. 8,32
Câu 5:
Tuổi các học viên của một lớp học Tiếng Anh tại một trung tâm được ghi lại ở bảng tần số ghép lớp như sau:
|
Lớp |
Tần số |
|
[16; 20) |
10 |
|
[20; 24) |
12 |
|
[24; 28) |
14 |
|
[28; 32) |
9 |
|
[32; 36) |
5 |
Khi đó độ lệch chuẩn của bảng số liệu là (kết quả làm tròn đến hàng phần chục):
A. 24,8
B. 5,3
C. 5,0
D. 25,0
Câu 6:
Cho mẫu số liệu thống kê: {5; 2; 1; 6; 7; 5; 4; 5; 9}. Mốt M0 của mẫu số liệu trên bằng bao nhiêu?
A. 3
B. 5
C. 9
D. 7
Câu 7:
Cho mẫu số liệu thống kê {6; 4; 4; 1; 9; 10; 7}. Số liệu trung vị của mẫu số liệu thống kê trên là:
A. 1
B. 6
C. 4
D. 10
Câu 8:
Có 100 học sinh tham dự kì thi HSG Toán (thang điểm 20 điểm) kết quả như sau:
|
Điểm |
9 |
10 |
11 |
12 |
13 |
14 |
|
Tần số |
2 |
1 |
2 |
10 |
8 |
8 |
|
Điểm |
15 |
16 |
17 |
18 |
19 |
Cộng |
|
Tần số |
24 |
18 |
14 |
10 |
3 |
100 |
Tính độ lệch chuẩn (kết quả làm tròn đến hai chữ số thập phân).
A. 4,67
B. 2,16
C. 4,70
D. 2,17
Câu 9:
Ba nhóm học sinh gồm 20 người,15 người,25 người.Khối lượng trung bình của mỗi nhóm lần lượt là 50kg,38kg,40kg.Khối lượng trung bình của cả ba nhóm học sinh là
A. 41,6 kg
B. 42,8 kg
C. 41,8 kg
D. Đáp số khác
Câu 10:
Cho dãy số liệu thống kê: 48,36,33,38,32,48,42,33,39. Khi đó số trung vị là
A. 32
B. 36
C. 38
D. 40
Câu 11:
Cho mẫu số liệu thống kê .Mốt của mẫu số liệu trên bằng bao nhiêu?
A. 5
B. 10
C. 2
D. 6
Câu 12:
Cho mẫu số liệu thống kê .Trung vị của mẫu số liệu trên là bao nhiêu?
A. 14
B. 16
C. 17
D. 18
Câu 13:
Điểm thi học kì của một học sinh như sau:4;6;2;7;3;5;9;8;7;10;9. Số trung bình và số trung vị lần lượt là
A. 6,22 và 7
B. 7 và 6
C. 6,4 và 7
D. 6 và 6
Câu 14:
Cho mẫu số liệu thống kê .Số trung bình của mẫu số liệu trên là
A. 12
B. 14
C. 13
D. 12,5
Câu 15:
Ba nhóm học sinh gồm 20 người,15 người,25 người.Khối lượng trung bình của mỗi nhóm lần lượt là 50kg,38kg,40kg.Khối lượng trung bình của cả ba nhóm học sinh là
Câu 16:
Cho dãy số liệu thống kê: 48,36,33,38,32,48,42,33,39. Khi đó số trung vị là
Câu 17:
Cho mẫu số liệu thống kê .Mốt của mẫu số liệu trên bằng bao nhiêu?
A. 5
B. 10
C. 2
D. 6
Câu 18:
Cho mẫu số liệu thống kê .Trung vị của mẫu số liệu trên là bao nhiêu? {28, 16, 13, 18, 12, 28, 13, 19}
Câu 19:
Điểm thi học kì của một học sinh như sau:4;6;2;7;3;5;9;8;7;10;9. Số trung bình và số trung vị lần lượt là
Câu 20:
Cho dãy số liệu thống kê:21, 23, 24, 25, 22, 20.Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 22
B. 22,5
C. 23,5
D. 14
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.