Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Giá trị lượng giác của cung (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Giá trị lượng giác của cung (50 bài tập minh họa) HAY NHẤT 2024
1. Lý thuyết
a. Định nghĩa:
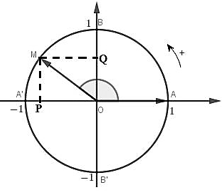
Trên đường tròn lượng giác cho cung có sđ , khi đó:
+) Tung độ của M gọi là sin của , kí hiệu là :
+) Hoành độ của M gọi là cosin của , kí hiệu là :
+) Nếu , tỉ số gọi là tang của , kí hiệu là :
+) Nếu , tỉ số gọi là côtang của , kí hiệu là :
Các giá trị ,,, được gọi là các giá trị lượng giác của cung . Ta cũng gọi trục tung là trục sin, trục hoành là trục cosin.
b. Hệ quả:
+) xác định với mọi giá trị của và .
+) được xác định khi , xác định khi
+)
+) Dấu của các giá trị lượng giác phụ thuộc vào vị trí điểm M nằm trên đường tròn lượng giác.
Ta có bảng xác định dấu của các giá trị lượng giác:
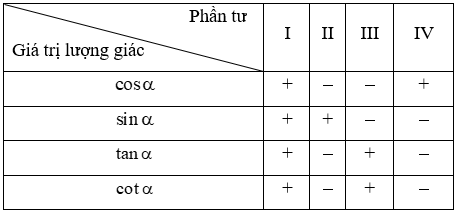
c. Giá trị lượng giác của các cung đặc biệt:
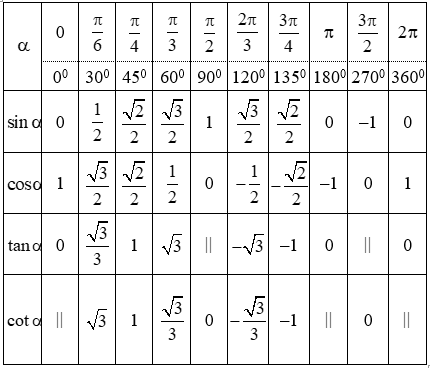
d. Các công thức lượng giác cơ bản:

e. Giá trị lượng giác của góc (cung) có liên quan đặc biệt:
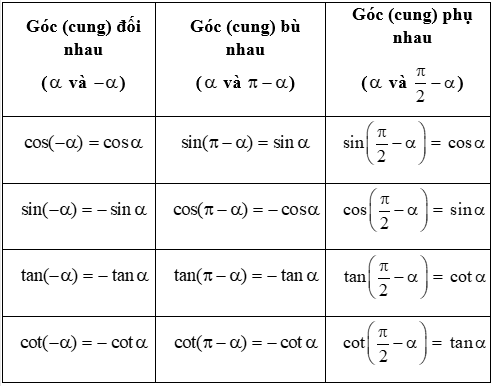
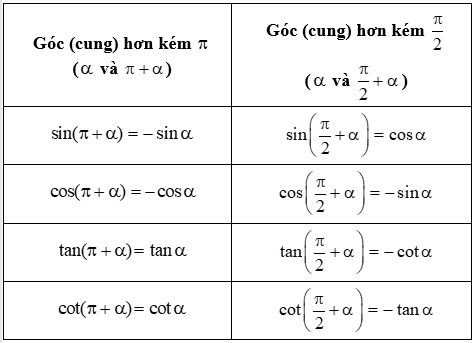
2. Các dạng bài
Dạng 2.1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị
a. Phương pháp giải:
Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.
b. Ví dụ minh họa:
Ví dụ 1: Cho với . Tính các giá trị lượng giác còn lại của góc .
Hướng dẫn:
Ta có:
Do nên . Suy ra, .
Từ đó, suy ra: ;
.
Ví dụ 2: Cho với . Tính các giá trị lượng giác còn lại của góc .
Hướng dẫn:
Ta có:
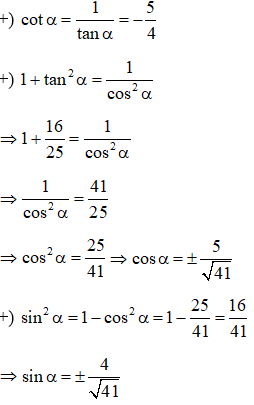
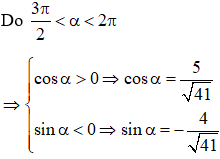
Dạng 2.2: Chứng minh một đẳng thức giữa các giá trị lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
b. Ví dụ minh họa:
Ví dụ 1: Chứng minh rằng:
a.
b.
Hướng dẫn:
a. Ta có:
Suy ra đpcm.
b. Ta có:
Suy ra đpcm.
Ví dụ 2: Chứng minh rằng: với .
Hướng dẫn:
Ta có:
Suy ra đpcm.
Dạng 2.3: Rút gọn biểu thức lượng giác
a. Phương pháp giải:
Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
b. Ví dụ minh họa:
Ví dụ 1: Rút gọn các biểu thức:
a.
b.
Hướng dẫn:
a. Ta có:
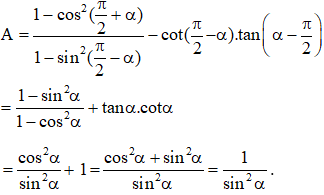
b. Ta có:
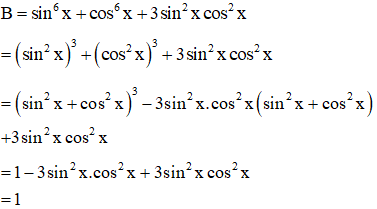
Ví dụ 2: Rút gọn biểu thức: .
Hướng dẫn:
Ta có:
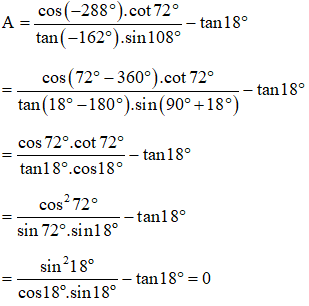
3. Bài tập vận dụng
Câu 1: Cho với . Tính giá trị .
Hướng dẫn:
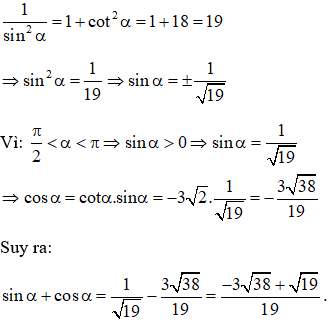
Câu 2: Cho và . Tính giá trị của .
Hướng dẫn:
Từ
Mặt khác: . Thế (1) vào (2), ta được:
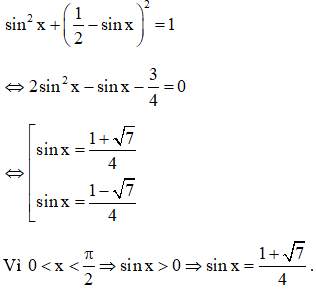
Câu 3: Cho và nhận giá trị âm, tính giá trị của biểu thức .
Hướng dẫn:
Vì nhận giá trị âm.
Ta có:
Suy ra:
Câu 4: Rút gọn biểu thức A = .
Hướng dẫn:
Ta có:
Câu 5: Rút gọn biểu thức .
Hướng dẫn:
Ta có:
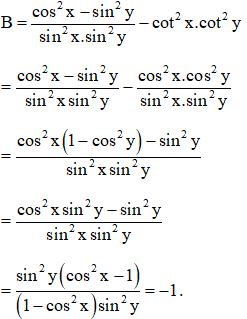
Câu 6: Rút gọn biểu thức:
Hướng dẫn:
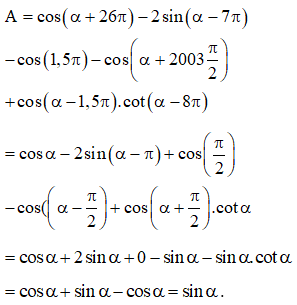
Câu 7: Chứng minh rằng với , .
Hướng dẫn:
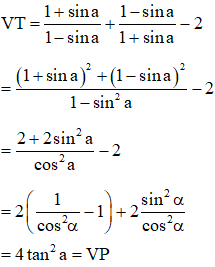
Suy ra đpcm.
Câu 8: Chứng minh đẳng thức sau: .
Hướng dẫn:
Ta có:
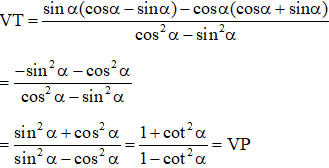
Câu 9: Cho cung lượng giác có số đo x thỏa mãn . Giá trị của biểu thức .
Hướng dẫn:
Do . Chia cả tử và mẫu của biểu thức cho , ta được:
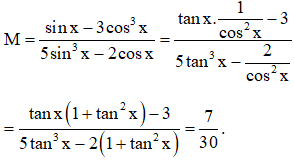
Câu 10: Rút gọn biểu thức .
Hướng dẫn:
Ta có
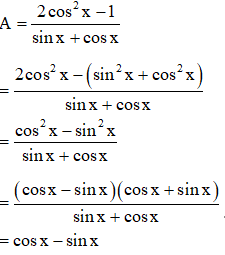
4. Bài tập tự luyện
Bài 1: Cho 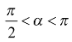 . Xác định tính âm dương của các giá trị lượng giác:
. Xác định tính âm dương của các giá trị lượng giác:

Hướng dẫn: Xác định điểm cuối của các cung ,… thuộc cung phần tư nào, từ đó xác định tính âm dương của các giá trị lượng giác tương ứng.
+ Cách xác định tính âm dương của các giá trị lượng giác
Giải
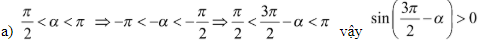
Bài 2: Tính các giá trị lượng giác của góc α biết:

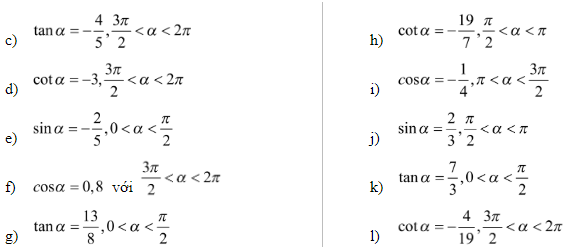
Hướng dẫn:
+ Nếu biết trước sinα thì dùng công thức: sin2α + cos2α = 1 để tìm ,
lưu ý:xác định dấu của các giá trị lượng giác để nhận, loại.
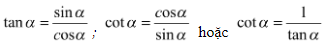
+ Nếu biết trước cosα thì tương tự như trên.
+ Nếu biết trước tanα thì dùng công thức: 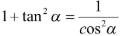 để tìm cosα ,
để tìm cosα ,
lưu ý: xác định tính âm dương của các giá trị lượng giác để nhận, loại. sinα = tanα.cosα ,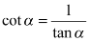
Giải
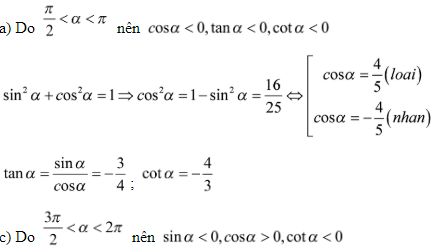
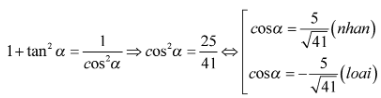
Các bài tập còn lại làm tương tự.
Bài 3: Chứng minh đẳng thức lượng giác: (dùng các hằng đẳng thức đại số và các hằng đẳng thức lượng giác cơ bản để biến đổi một vế thành vế kia)
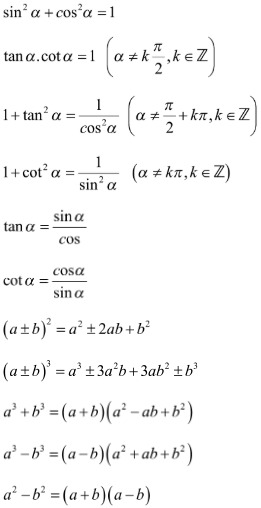
Hướng dẫn:
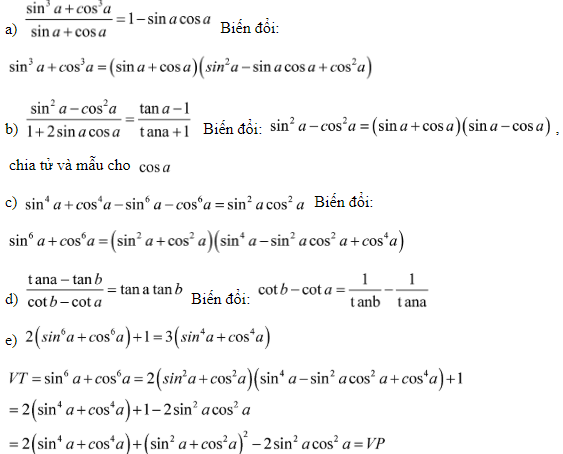
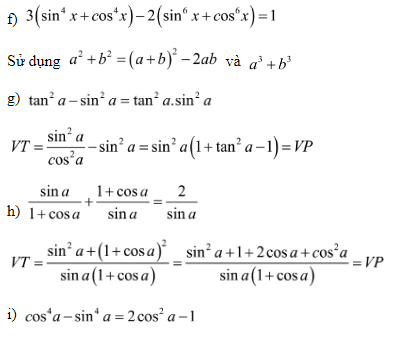
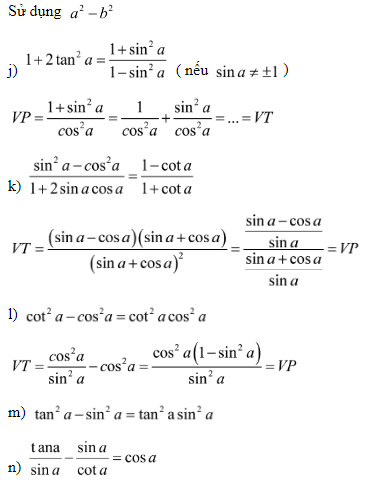
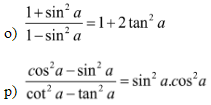
Nhận xét: Trong tài liệu bài tập lượng giác lớp 10 cơ bản có đáp án thì đây là một dạng bài khá hay vì nó kết hợp giữa các hằng đẳng thức đại số và các công thức lượng giác. Để nhận dạng các bài tập loại này các em cần lưu ý các hằng đẳng thức mà chúng ta thường gặp là:
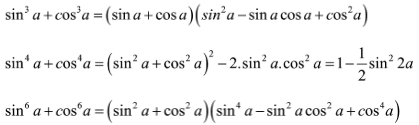
Bài 4: Đơn giản các biểu thức sau:
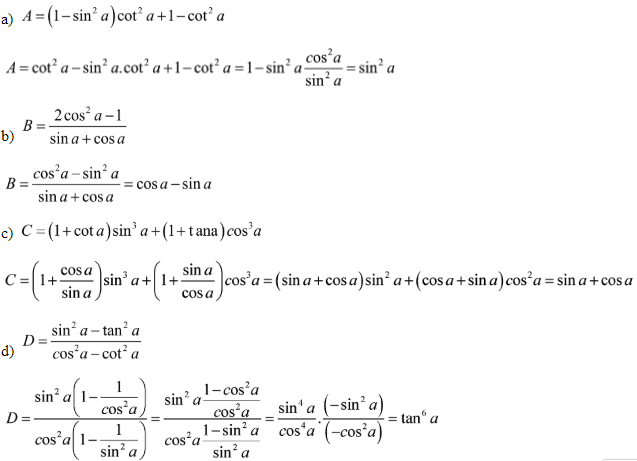
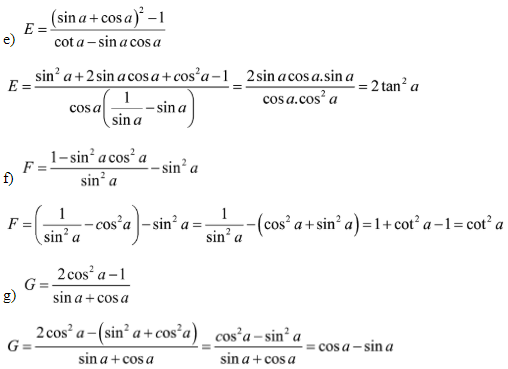
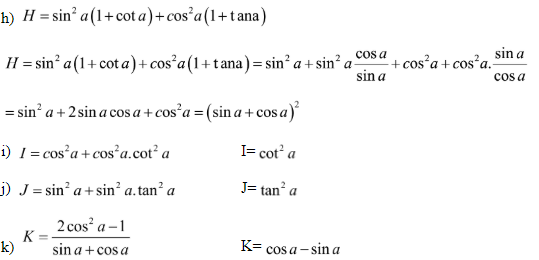
Bài 5: Cho 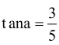 . Tính:
. Tính:
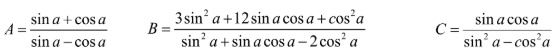
Hướng dẫn: Để tính các biểu thức này ta phải biến đổi chúng về một biểu thức theo tana rồi thay giá trị của tan a vào biểu thức đã biến đổi.

Bài 6: Cho 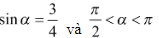 . Tính:
. Tính:

Hướng dẫn:
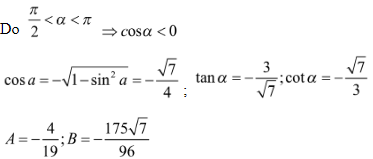
Bài 7: Cho 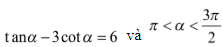 và . Tính:
và . Tính:

Hướng dẫn:
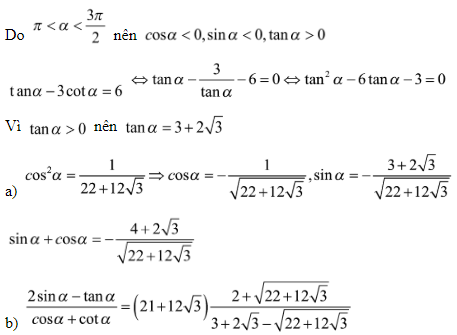
Bài 8: Cho 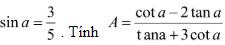
Hướng dẫn: Biến đổi biểu thức A theo sin2α
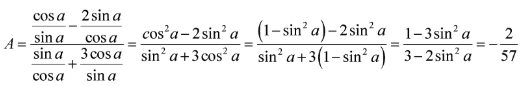
Bài 9:
a) Tính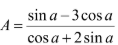 biết tanα = -3
biết tanα = -3
b) Tính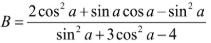 biết cotα = 2
biết cotα = 2
Hướng dẫn: a) Chia cả tử và mẫu cho cosα
b) Chia cả tử và mẫu cho sinα
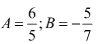
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Giá trị lượng giác của cung và cách giải bài tập
Công thức lượng giác chi tiết và cách giải bài tập
Các định nghĩa về vectơ và cách giải bài tập
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.